Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
345
TỐI ƯU HOẠT ĐỘNG HỆ THỐNG PHẢN ỨNG
SỬ DỤNG TỐI ƯU PHI TUYẾN
Phạm Đức Đại
Trường Đại học Thủy lợi, email: daipd@tlu.edu.vn
1. ĐIỀU KHIỂN QUÁ TRÌNH
Điều khiển tối ưu các quá trình trong công
nghiệp được xây dựng như các bài toán điều
khiển tối ưu phi tuyến tính (OCP). Các
phương pháp tối ưu hóa để giải OCP có thể
được phân loại thành các phương pháp tối ưu
hóa gián tiếp và trực tiếp. Trong phương
pháp đầu tiên, được gọi là phương pháp trực
tiếp hoặc phương pháp biến thiên, điều kiện
tối ưu của OCP dẫn đến một bài toán giá trị
hai điểm biên mà chỉ có thể giải được đối với
các OCP không có ràng buộc bất đẳng thức.
Trong khi đó, trong phương pháp trực tiếp,
một bài toán OCP hữu hạn (tức là có ràng
buộc về đẳng thức và bất đẳng thức) được rời
rạc thành bài toán tối ưu phi tuyến tính vô
hạn (NLP), bài toán này có thể được giải hiệu
quả bằng thuật toán giải bài toán tối ưu phi
tuyến. Có hai phương pháp phổ biến để rời
rạc hóa bài toán tối ưu đó là: phương pháp
collocation [1] và phương pháp multiple
shooting [2]. Bài báo trình bày phương pháp
rời rạc hóa nhiều điểm (multiple shooting) và
áp dụng để tối ưu hóa quá trình phản ứng
nhiệt [4]. Để thực hiện việc giải bài toán tối
ưu, công cụ phần mềm CasaDi [3] để giải bài
toán tối ưu sau khi đã rời rạc.
2. BÀI TOÁN TỐI ƯU
Bài toán điều khiển tối ưu tổng quát được
cho như sau với các phương trình vi phân thể
hiện hệ thống:
x
tfxt,ut (1)
ở đó:
n
x
xt là trạng thái và
nu
ut là
đại lượng điều khiển. Hàm mục tiêu được
viết dưới dạng tổng quát như say:
 




0
0
tf
f
J
lx ,u d x ,xt


(2)
ở đó:
l
hàm mục tiêu;
0f
x
,x t
là giá
trị cuối.
g
xt,ut thể hiện ràng buộc của
bài toán tối ưu:
 
 




0
0
tf
f
x.,u.
minlx,u d x,xt

0
x
tfxt,ut, tt
 (3)
00
f
g
xt,ut , t t

L
U
x
xt x
Rời rạc hóa bài toán tối ưu
Bài toán điều khiển tối ưu (OCP) là vô
hạn, nó được rời rạc hóa thành bài toán tối ưu
hóa phi tuyến tính rời rạc hoặc hữu hạn
(NLP). Trong bài báo này, chúng tôi chọn
phương nhiều điểm để rời rạc hóa [9].
Các biến điều khiển được phân chia thành
các hằng số từng phần trên mỗi khoảng thời
gian, như:
1iii
u t q for t t ,t
 (4)
Trong mỗi khoảng thời gian, tức là
1ii
t,t
,
ODE được giải quyết bằng một giá trị khởi
tạo nhân tạo i
s
được coi là một biến tối ưu
hóa. ODE và giá trị khởi tạo cần được giải
quyết là:

1
iiiii
ii i
x
tfxt,q, tt,t
xt s.

(5)
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
346
ODE này có thể được giải quyết bằng RK 4.
Và chúng ta cũng tính toán các tích phân sau:


1
ti
i ii iiii i
ti
l s ,q : L x t ;s ,q ,q dt
(6)
Giả sử

1ii ii
x
t;s,q
là nghiệm của ODE đối
với
1ii
tt,t
Để đảm bảo tính liên tục, các
ràng buộc sau phải được thỏa mãn.

11iiiii
s
xt ;s,q

(7)
Bài toán tối ưu phi tuyến được rời rạc hóa
theo phương pháp nhiều điểm được viết lại
như sau:

1
0
N
iii N
s,q i
minimize l s ,q E s
00
0sx

11 00 1
iiiii
sxt;s,q ;i,,N

 (8)

00
ii
g
s,q , i , ,N
Để giải bài toán tối ưu trên, phần mềm
Ipopt được sử dụng, đây là phần mềm giải
bài toán tối ưu phi tuyến.
3. ÁP DỤNG
CSTR thực hiện phản ứng nhiệt [4]. Hệ
thống bao gồm ba biến trạng thái, đó là nồng
độ chất phản ứng (x2), mức chất lỏng (x1).
Các trạng thái này được kiểm soát bởi nồng
độ chất phản ứng cấp vào bể chứa u1 (mol/m3).
Đây là biến điều khiển. Bài toán tối ưu như sau:
  


  
 
 
2
2
1
21
2
2
0
05
01 00
001
01
x,u f
l
l
l
f
min J x t
s.t.
dx t ut .u t x t
dt
dx t utx t
dt
x,x
xt, x t
t,t





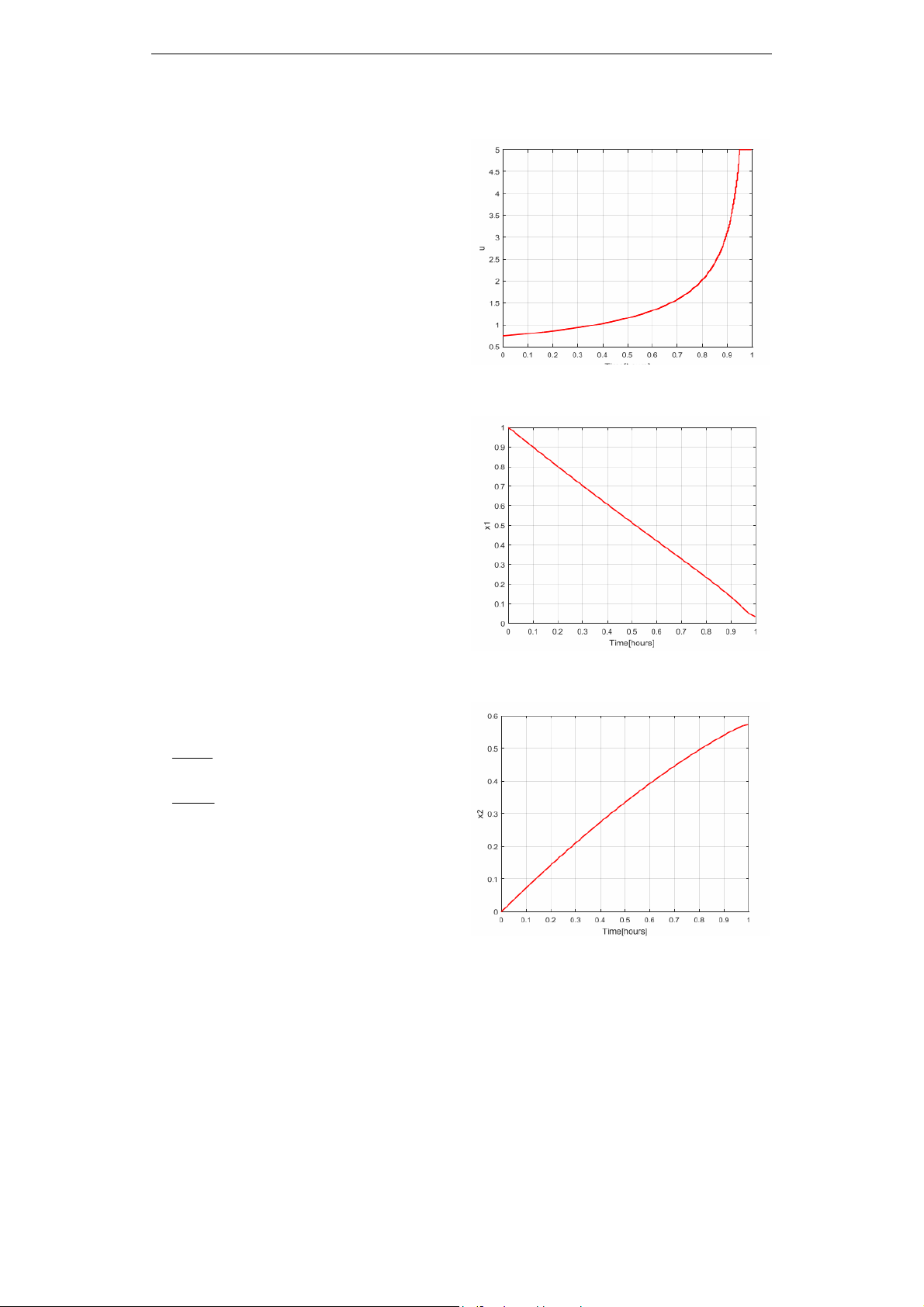
Kết quả các trạng thái hệ thống được cho
trên Hình 2, và Hình 3 tương ứng cho các
trạng thái x1 và x2. Đại lượng điều khiển
được cho trên Hình 1. Có thể thấy, sau một
khoảng thời gian thì tín hiệu điều khiển xác
lập tại giá trị bằng 5.
Hình 1. Đại lượng điều khiển
Hình 2. Biến trạng thái x1
Hình 3. Biến trạng thái x2
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
347
Biến thiên của các biến trạng thái x1 từ
giá trị 1 đến gần giá trị 0 (ở Hình 2), trong
khi biến trạng thái x2 biến thiên từ 0 đến giá
trị 0.57 (ở Hình 3). Giá trị của hàm mục tiêu
là -0.57.
4. KẾT LUẬN
Bài báo đã trình bày phương pháp rời rạc
hóa bài toán tối ưu phi tuyến sử dụng phương
pháp nhiều điểm (multishooting). Bài toán tối
ưu sau khi được rời rạc hóa được giải bằng
phần mềm Ipopt và áp dụng vào giải bài toán
tối ưu điều khiển quá trình. Kết quả cho thấy
phương pháp rời rạc hóa nhiều điểm cho thời
gian tính toán nhanh.
5. TÀI LIỆU THAM KHẢO
[1] Biegler, L. T. (2007). An overview of
simultaneous strategies for dynamic
optimization. Chemical Engineering and
Processing: Process Intensification, 46(11),
1043-1053.
[2] Bock, H. G., & Plitt, K. J. (1984). A
multiple shooting algorithm for direct
solution of optimal control problems. IFAC
Proceedings Volumes, 17(2), 1603-1608.
[3] Andersson, J. A., Gillis, J., Horn, G., Rawlings,
J. B., & Diehl, M. (2019). CasADi: a software
framework for nonlinear optimization and
optimal control. Mathematical Programming
Computation, 11, 1-36.
[4] Tamimi, Jasem, and Pu Li. "A combined
approach to nonlinear model predictive
control of fast systems." Journal of Process
Control 20.9 (2010): 1092-1102.