Outline
1. Mạch logic số (Logic circuit)
2. Thiết kế một mạch số
3. Bản đồ Karnaugh
4. Cổng XOR/XNOR ( XOR/XNOR gate)
Reading assignment:
Chương 4: section 4.3.4, 4.3.5, 4.3.6, 4.3.7, 4.3.8
Khoa KTMT 1
1. Mạch logic số (logic circuit)
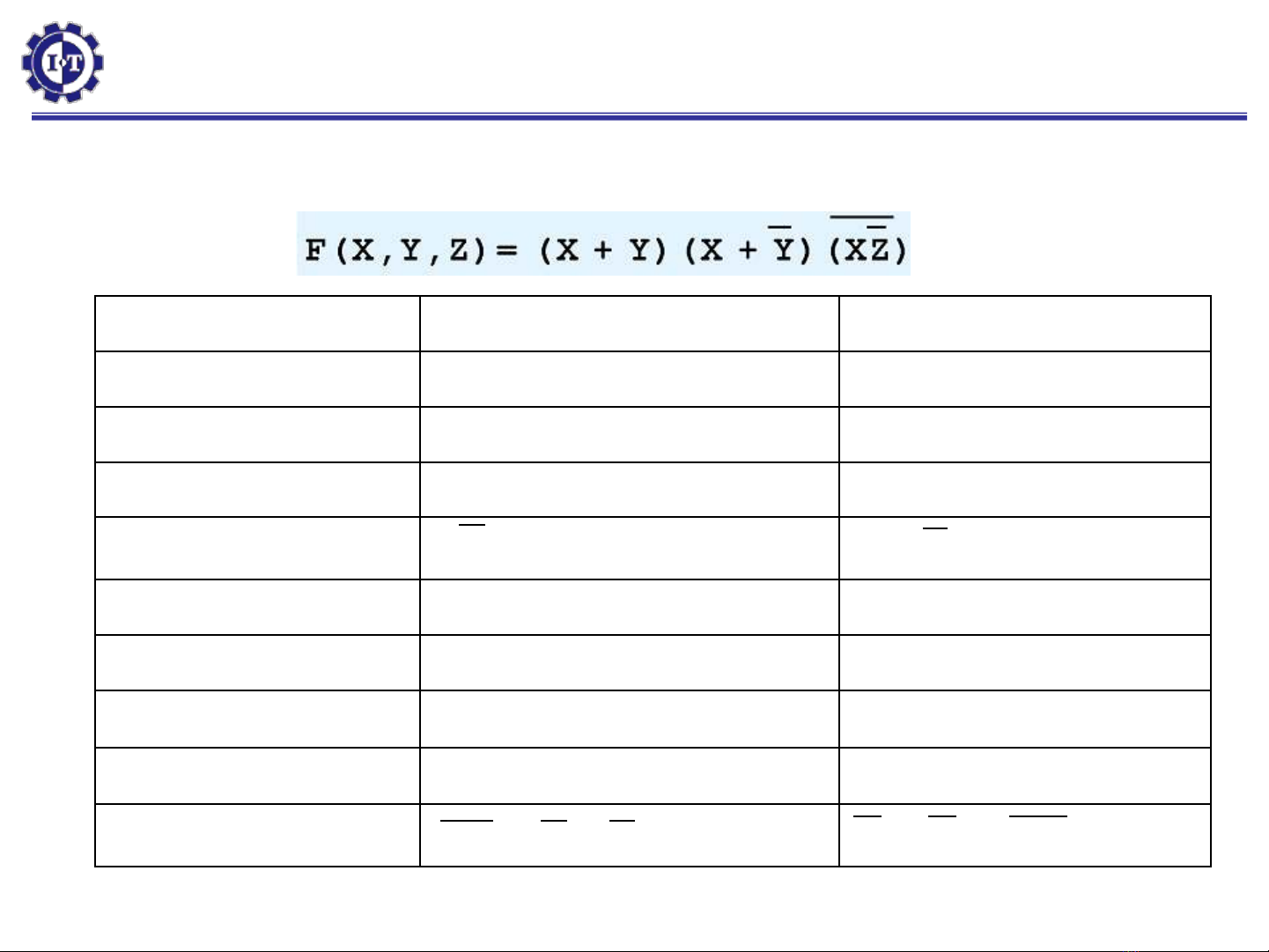
Dùng định lý Boolean để đơn giản hàm sau:
Khoa KTMT 2
Tên Dạng AND Dạng OR
Định luật thống nhất 1A = A 0 + A = A
Định luật không OA = O 1+ A = 1
Định luật Idempotent AA = A A + A = A
Định luật nghịch đảo
Định luật giao hoán AB = BA A + B = B + A
Định luật kết hợp (AB)C = A(BC) (A+B)+C = A + (B+C)
Định luật phân bố A + BC = (A + B)(A + C) A(B+C) = AB + AC
Định luật hấp thụ A(A + B) = A A + AB = A
Định luật De Morgan
0AA
1 AA
BAAB
ABBA
Khoa KTMT 3
Dạng chính tắc và dạng chuẩn của hàm Boole
Tích chuẩn (minterm): mi (0 ≤ i 2n-1) là các số hạng tích (AND) của n
biến mà hàm Boole phụ thuộc với quy ước biến đó có bù nếu nó là 0 và
không bù nếu là 1.
Tổng chuẩn (Maxterm): Mi (0 ≤ i 2n-1) là các số hạng tổng (OR) của n
biến mà hàm Boole phụ thuộc với quy ước biến đó có bù nếu nó là 1 và
không bù nếu là 0
Khoa KTMT 4
Dạng chính tắc (Canonical Form)
Dạng chính tắc 1: là dạng tổng của các tích chuẩn_1 (minterm_1 là minterm
mà tại tổ hợp đó hàm Boole có giá trị 1).
Khoa KTMT 5
Dạng chính tắc (Canonical Form) (tt)
Dạng chính tắc 2: là dạng tích của các tổng chuẩn_0
(Maxterm_0 là Maxterm mà tại tổ hợp đó hàm Boole có giá trị
0).
Trường hợp tùy định (don’t care)
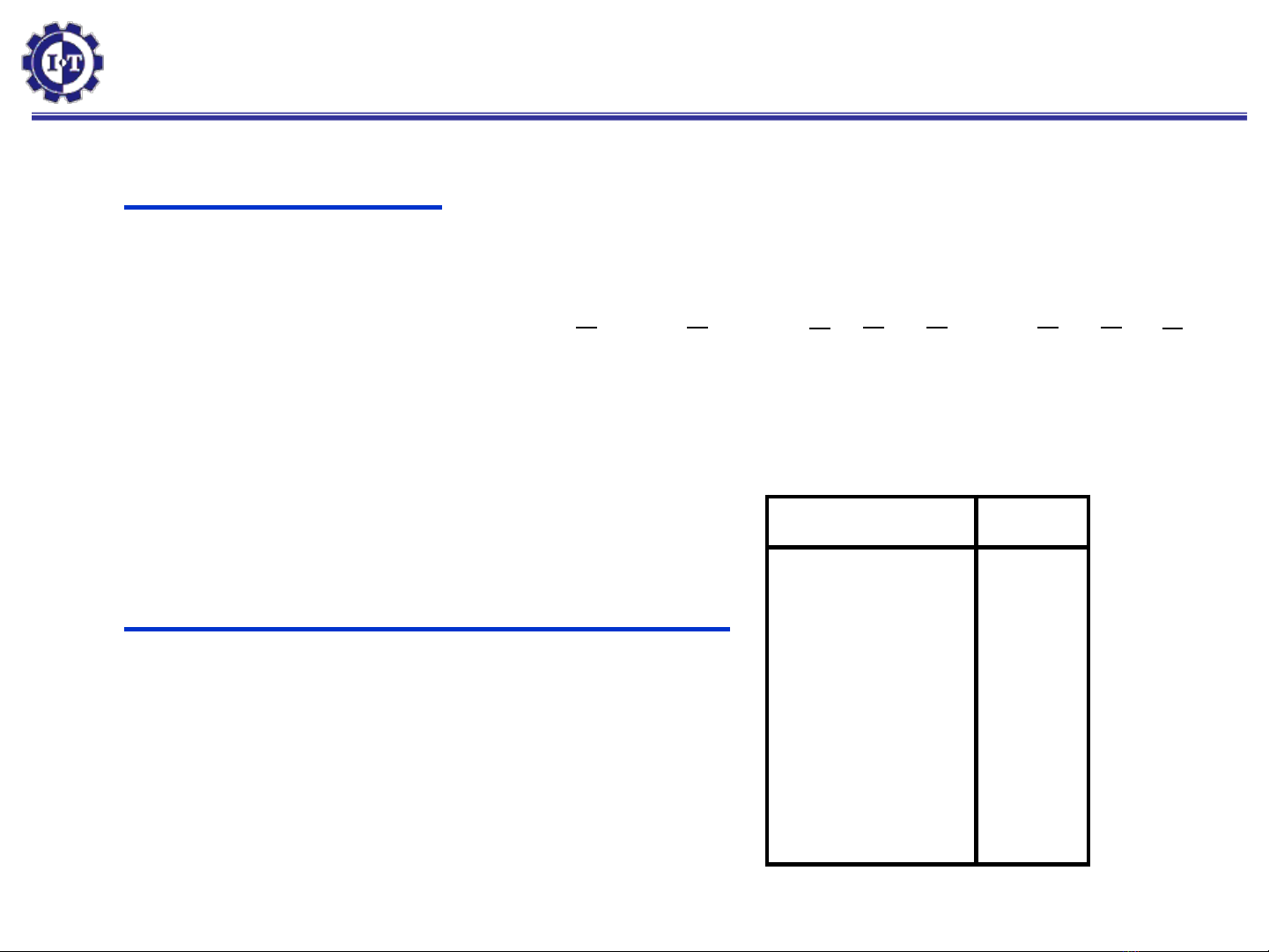
Hàm Boole theo dạng chính tắc:
F (A, B, C) =
(2, 3, 5) + d(0, 7)
=
(1, 4, 6) . D(0, 7)
A B C F
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
X
0
1
1
0
1
0
X
0 2 5 6 7
( , , ) ( )( )( )( )( )F x y z x y z x y z x y z x y z x y z
M M M M M
0 2 5 6 7
( , , )
(0,2,5,6,7)
F x y z M M M M M