
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN KINH TẾ VÀ QUẢN LÝ
CHƯƠNG 5:
ƯỚC LƯỢNG VÀ KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ VỀ
THAM SỐ TỔNG THỂ
EM3230 THỐNG KÊ ỨNG DỤNG TRONG KINH DOANH

EM3230 Thống kê ứng dụng
Nội dung chính
5.1 Phân phối của các tham số mẫu (Bài giảng video)
5.2 Lý thuyết về ước lượng và kiểm định
5.3 Ước lượng và kiểm định giả thuyết trên một tổng thể (Bài giảng video)
5.4 Ước lượng và kiểm định giả thuyết trên hai tổng thể (Bài giảng video)
5.5 Xác định cỡ mẫu cho bài toán ước lượng và kiểm định
5.6 Ứng dụng kiểm định khi ra quyết định kinh doanh
2

EM3230 Thống kê ứng dụng
Nội dung chính
5.1 Phân phối của các tham số mẫu (Bài giảng video)
5.2 Lý thuyết về ước lượng và kiểm định (Bài giảng video)
5.3 Ước lượng và kiểm định giả thuyết trên một tổng thể (Bài giảng video)
5.4 Ước lượng tỷ lệ cho một tổng thể
5.5 Ước lượng phương sai tổng thể
5.6 Xác định cỡ mẫu cho bài toán ước lượng
5.7 Ước lượng trên hai mẫu (Bài giảng video)
3

EM3230 Thống kê ứng dụng
Mục tiêu của chương
Sau khi học xong chương này người học có thể:
§Nắm được những vấn đề cơ bản về phân phối của hai đại lượng chính của mẫu là trung bình
mẫu và tỷ lệ mẫu
§Hiểu ýnghĩa của hệ số hiệu chỉnh tổng thể hữu hạn trong việc điều chỉnh độ lệch chuẩn của
trung bình mẫu và tỷ lệ mẫu
§Nắm được các khái niệm: Khoảng tin cậy, độ tin cậy, mức ýnghĩa alpha, và mối liên hệ giữa
tham số mẫu và tham số tổng thể
§Biết cách xác định ước lượng khoảng và kiểm định cho trung bình
§Hiểu phân phối Student và biết cách tra bảng xác suất phân phối student
§Biết cách xác định cỡ mẫu khi cần hạn chế sai số do lấy mẫu
§Biết cách xác định ước lượng khoảng và kiểm định đối với các chênh lệch trung bình và tỷ lệ
của hai tổng thể
4
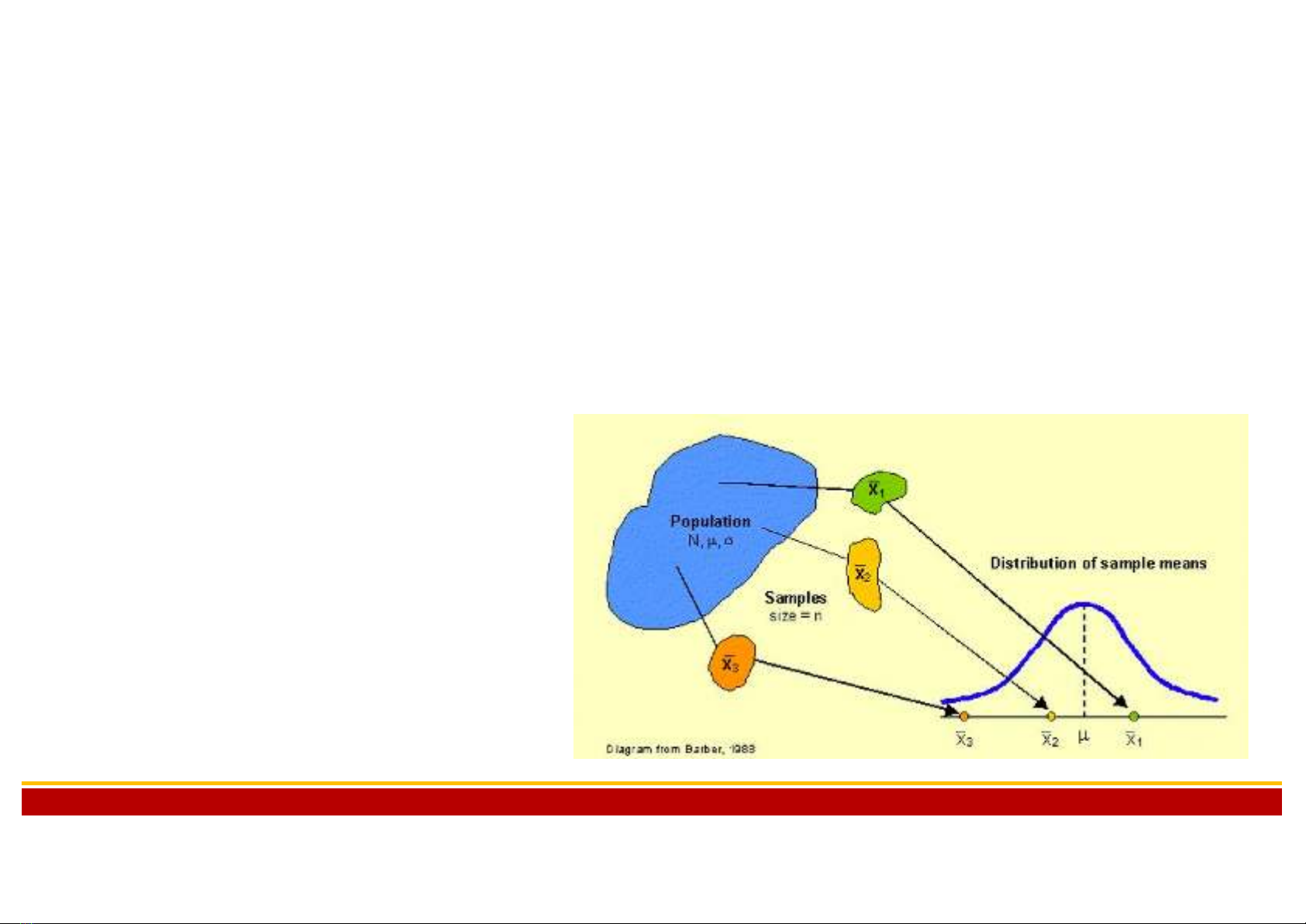
EM3230 Thống kê ứng dụng
5.1 Phân phối của tham số mẫu
5.1.1 Giới thiệu chung về phân phối của tham số mẫu
5.1.2 Phân phối của trung bình mẫu
5.1.3 Phân phối của tỷ lệ mẫu
5











