CAÙC BAØI TAÄP PASCAL HAY
DAØNH CHO HS LÔÙP 9
BAØI 1 : XẾP GẠCH.
Minh r t thích trò ch i x p các chi c h p có hình viên g ch. Minh đ t các viên g chấ ơ ế ế ộ ạ ặ ạ
ch ng lên nhau và xây thành nhi u ch ng có đ cao khác nhau. Minh khoe v i ch r ngồ ề ồ ộ ớ ị ằ
“Ch trông, em đã xây đ c m t b c t ng”. Ch c a Minh tr l i “Em ph i x p các viênị ượ ộ ứ ườ ị ủ ả ờ ả ế
g ch có đ cao gi ng nhau m i đ c g i là m t b c t ng”. Sau khi nghe ch nói nh v yạ ộ ố ớ ượ ọ ộ ứ ườ ị ư ậ
nó cân nh c m t tí và cho r ng ý ki n y là đúng. Vì v y em b t đ u ti n hành s p x pắ ộ ằ ế ấ ậ ắ ầ ế ắ ế
l i các ch ng g ch l n l t t ng chi c m t cho đ n khi hoàn thành công vi c. Khi côngạ ồ ạ ầ ượ ừ ế ộ ế ệ
vi c đã hoàn t t, Minh m t l và mu n có b n nào giúp Minh di chuy n các viên g ch v iệ ấ ệ ả ố ạ ể ạ ớ
s l n ít nh t.ố ầ ấ
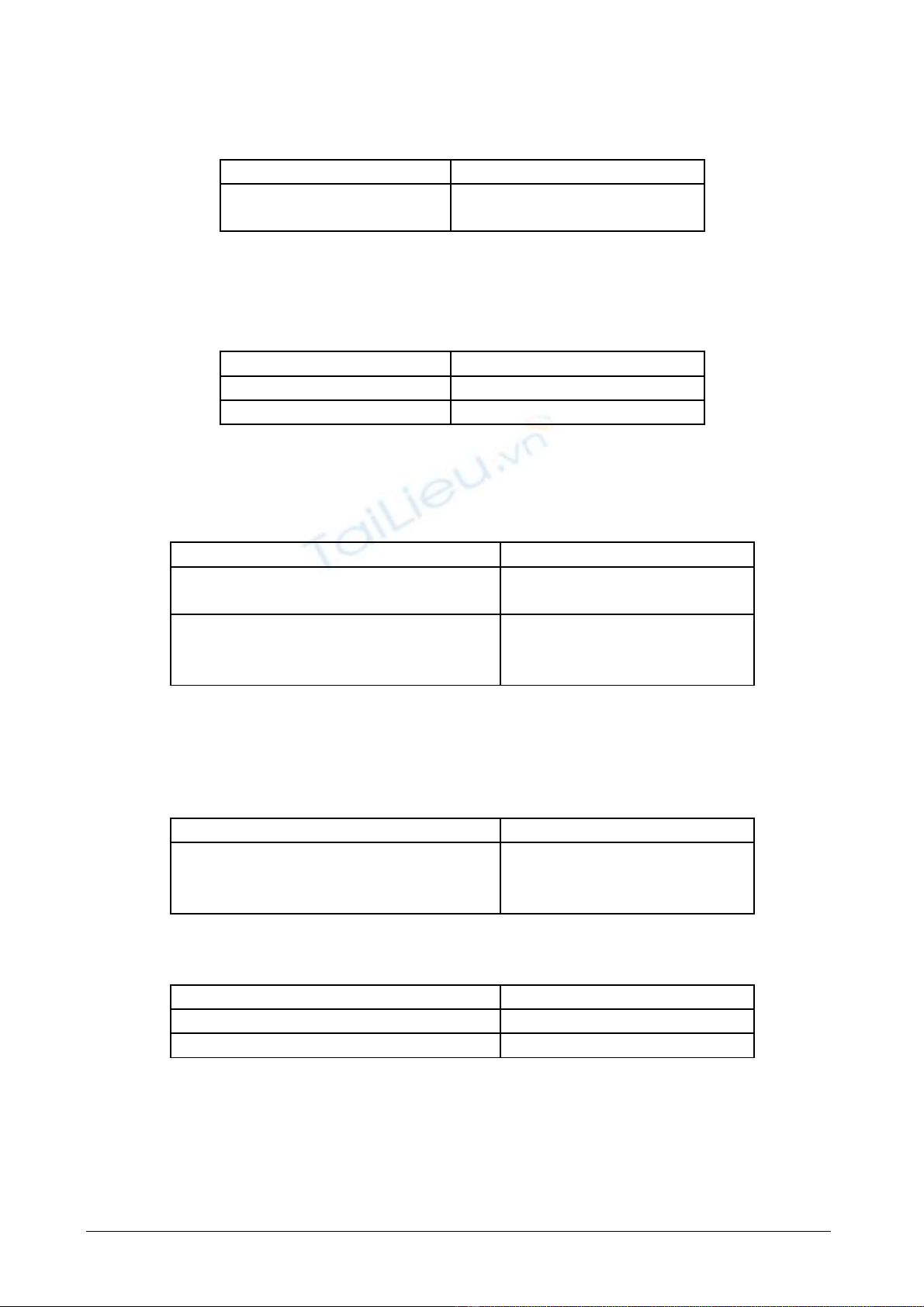
Các chi c h p tr c và sau khi x pế ộ ướ ế
Yêu c u:ầ Hãy l p trình đ a ra s l n di chuy n ít nh t c a các viên g ch sao cho tậ ư ố ầ ể ấ ủ ạ ừ
các ch ng g ch có đ cao khác nhau tr thành các ch ng g ch có đ cao b ng nhau; l nồ ạ ộ ở ồ ạ ộ ằ ầ
l t t ng chi c m t cho đ n khi hoàn thành công vi c. ượ ừ ế ộ ế ệ
D li u vào:ữ ệ có c u trúc sau:ấ
- dòng đ u tiên là s n, n là s các ch ng g ch,ầ ố ố ồ ạ
- dòng ti p theo l n l t là các hế ầ ượ i, đ cao c a ch ng g ch th i. (1≤ n ≤ 50; 1≤ hộ ủ ồ ạ ứ i ≤
100; i = 1..n). L u ý r ng s viên g ch bao gi cũng chia h t cho s ch ng g ch.ư ằ ố ạ ờ ế ố ồ ạ
D li u ra:ữ ệ ch có m t dòng ch a m t s nguyên d ng là k t qu tính toán s l nỉ ộ ứ ộ ố ươ ế ả ố ầ
ít nh t sau khi x p l i các ch ng g ch. N u không có k t qu cũng ph i ghi rõ “KHONGấ ế ạ ồ ạ ế ế ả ả
CAN DI CHUYEN LAN NAO”
Ví d : v i hình trên ta có d li u vào, ra:ụ ớ ữ ệ
Input Output
6
5 2 4 1 7 5
5
7
9 9 9 9 9 9 9
Khong can di chuyen lan
nao
BAØI 2: SAÉP SOÁ TRONG XAÂU
Gv: Tr ần Minh Th ọ1/5
1. Nhaäp moät xaâu s bao goàm soá vaø kí töï, in ra xaâu ñaõ saép xeáp soá theo thöù töï
taêng daàn coøn vò trí caùc kí töï vaãn giöõ nguyeân?
Input Output
abc6ghj7kkkkk1hhhh9 abc6ghj7kkkkk1hhhh9
BAØI 3: KYÙ TÖÏ NHIEÀU NHAÁT
Nhaäp vaøo xaâu s (az), in ra kyù töï xuaát hieän nhieàu laàn nhaát trong xaâu vaø soá
laàn xuaát hieän? Neáu coù nhieàu tröôøng hôïp thì in ra tröôøng hôïp ñaàu tieân.
ví duï:
Input Output
abcaabca a 4
bcbsaaba b 3
BAØI 4: TÖØ DAØI NHAÁT
In ra töø daøi nhaát trong moät xaâu nhaäp töø baøn phím vaø soá kyù töï cuûa töø naøy?
Neáu coù nhieàu töø coù ñoä daøi baèng nhau thì in ra heát.
ví duï: Input Output
Nguyen van truong truong
4
Truong thich hoc pascal Truong
pascal
5
BAØI 5: DAÕY CON LÔÙN NHAÁT
Cho m t m ng s nguyên g m n ph n t . Tìm dãy con g m m ph n t (mộ ả ố ồ ầ ử ồ ầ ử ≤n) sao cho dãy
con này có t ng l n nh t. (Dãy con là dãy các ph n t liên ti p nhau trong m ng).ổ ớ ấ ầ ử ế ả
nh p n, nh p các ph n t c a dãy, nh p m, in ra dãy con có m ph n t .ậ ậ ầ ử ủ ậ ầ ử
Input Output
8
4 3 5 2 8 7 9 6
3
8 7 9
BAØI 6: XOAÙ KYÙ TÖÏ TRUØNG
Vieát chöông trình nhaäp vaøo 1 xaâu vaø xoaù heát caùc kyù töï lieân tieáp gioáng nhau
trong xaâu chæ chöøa laïi moät?
Input Output
cccccaaannnnooo cano
yeseeeyysss yeseys
BAØI 7: SOÁ ÑÔN ÑIEÄU
Gv: Tr ần Minh Th ọ2/5
Caùc soá nguyeân döông 3748, 58, 859, 32435465768 ñöôïc goïi laø caùc soá ñôn ñieäu do
neáu quan saùt caùc chöõ soá cuûa soá naøy , ta thaáy chuùng luaân phieân taêng giaûm
hoaëc giaûm taêng. Chaúng haïn:
3 < 7 > 4 < 8 vaø 3 > 2 < 4 > 3 < 5 > 4 < 6 > 5 < 7 > 6 < 8
Soá chæ coù moät chöõ soá laø soá ñôn ñieäu chieàu daøi 1.
Haõy vieát chöông trình xaùc ñònh soá chöõ soá ñaàu tieân lôùn nhaát taïo thaønh soá ñôn
ñieäu cuûa moät soá cho tröôùc.
Nhaäp vaøo moät soá nguyeân döông khoâng quaù 75 chöõ soá.
Xuaát ra soá chöõ soá ñaàu tieân lôùn nhaát taïo thaønh soá ñôn ñieäu.
Input Output
37486398 5
859672534163 12
BAØI 8: SOÁ NGUYEÂN TOÁ GHEÙP
Xét dãy A các số nguyên tố 2, 3, 5, 7, 11, 13, 17, 19,...
và dãy B gồm các số thu được từ dãy A bằng cách ghép hai số liên tiếp trong A: 23, 57,
1113, 1719, ...
Trong dãy B có những phần tử là số nguyên tố. Chẳng hạn 23, 3137, 8389, 157163...
Các số nguyên tố trong dãy B gọi là số nguyên tố ghép.
Yêu cầu: Cho trước số nguyên dương K ≤ 500, hãy tìm số nguyên tố ghép thứ K.
Input Output
2 3137
BAØI 9: TOÅNG 2 SOÁ NGUYEÂN TOÁ
Trong m t b c th mà Christian Goldbach g i cho Euler, ông ã c p n ộ ứ ư ử đ đề ậ đế
ph ng oán c a mình: M i s t nhiên ch n l n h n 2 u là t ng c a 2 s nguyên t . ỏ đ ủ ọ ố ự ẵ ớ ơ đề ổ ủ ố ố
Hãy l p ch ng trình ki m ch ng ph ng oán c a Goldbach. ậ ươ để ể ứ ỏ đ ủ
Yêu c u: ầ
- D li u vào t file GB.INP g m nhi u dòng, dòng u là s test (<10), các dòng ti pữ ệ ừ ồ ề đầ ố ế
theo m i dòng ghi 1 s t nhiên ch n l n h n 2 (<32000) ỗ ố ự ẵ ớ ơ
- D li u ra là file GB.OUT g m các dòng (m i dòng ng v i 1 test) - m i dòng ữ ệ ồ ỗ ứ ớ ỗ
g m 2 s nguyên t cách nhau ít nh t 1 d u cách có t ng b ng s ã cho (ho c không tìm ồ ố ố ấ ấ ổ ằ ố đ ặ
c – ghi là “khong”). đượ Input Output
3
8
12
5
3 5
5 7
2 3
BAØI 10: ÑÒNH LYÙ 6174
Dãy 6174 đ c t o theo cách sau. S h ng đ u tiên c a dãy là s nguyên d ng ượ ạ ố ạ ầ ủ ố ươ n1 g mồ
b n ch ố ữ
Gv: Tr ần Minh Th ọ3/5
s (b n ch s c a s h ng đ u tiên này không đ ng th i b ng nhau). Hai s m i (aố ố ữ ố ủ ố ạ ầ ồ ờ ằ ố ớ 1 và
b1) đ c ượ
t o thành t s đ u tiên c a dãy. S th nh t a1 có đ c b ng cách s p x p các ch sạ ừ ố ầ ủ ố ứ ấ ượ ằ ắ ế ữ ố
c a n1 theo ủ
th t gi m d n và s th nhì b1 có đ c b ng cách s p x p các ch s c a n1 theo thứ ự ả ầ ố ứ ượ ằ ắ ế ữ ố ủ ứ
t tăng ự
d n. S th nhì ầ ố ứ n2 c a dãy là hi u aủ ệ 1 - b1. Ti p t c, hai s aế ụ ố 2 và b2 đ c t o thành t nượ ạ ừ 2
t ng t ươ ự
nh aư1 và b1 và s th ba ố ứ n3 c a dãy 6174 là hi u aủ ệ 2 - b2, và c th ti p t c. Dãy s k tứ ế ế ụ ố ế
thúc khi
các s h ng c a dãy b t đ u l p l i (nghĩa là các ph n t c a dãy đôi m t khác nhau).ố ạ ủ ắ ầ ặ ạ ầ ử ủ ộ
Ch s 0 ữ ố ở
đ u s (v trí th nh t tính t bên trái) v n có nghĩa.ầ ố ị ứ ấ ừ ẫ
Đ nh lý 6174ị phát bi u r ng s h ng cu i c a dãy s xây d ng nh trên luôn là s 6174.ể ằ ố ạ ố ủ ố ự ư ố
Ch ng h n, xét dãy mà s h ng đ u tiên (n1) là 7815. Ta có:ẳ ạ ố ạ ầ
8751 - 1578 = 7173 (n2)
7731 - 1377 = 6358 (n3)
6543 - 3456 = 3087 (n4)
8730 - 0378 = 8352 (n5)
8532 - 2358 = 6174 (n6)
Bài toán:
Cho tr c s h ng đ u tiên c a dãy 6174. Cho bi t ch s c a s h ng cu i (là s h ngướ ố ạ ầ ủ ế ỉ ố ủ ố ạ ố ố ạ
6174) c a ủ
dãy.
D li u:ữ ệ
Cho trong t p tin văn b n DL6174.INP, g m m t dòng g m s nguyên d ng duy nh t làậ ả ồ ộ ồ ố ươ ấ
s ố
h ng đ u tiên c a dãy s 6174.ạ ầ ủ ố
K t qu :ế ả
Cho trong t p tin văn b n DL6174.OUT, g m m t dòng g m s nguyên d ng duy nh t làậ ả ồ ộ ồ ố ươ ấ
s ố
hi u c a s h ng cu i c a dãy s 6174 mà s h ng đ u cho trong t p tin d li u.ệ ủ ố ạ ố ủ ố ố ạ ầ ậ ữ ệ
Ví d :ụ
DL6174.INP DL6174.OUT
7815 6
Gv: Tr ần Minh Th ọ4/5
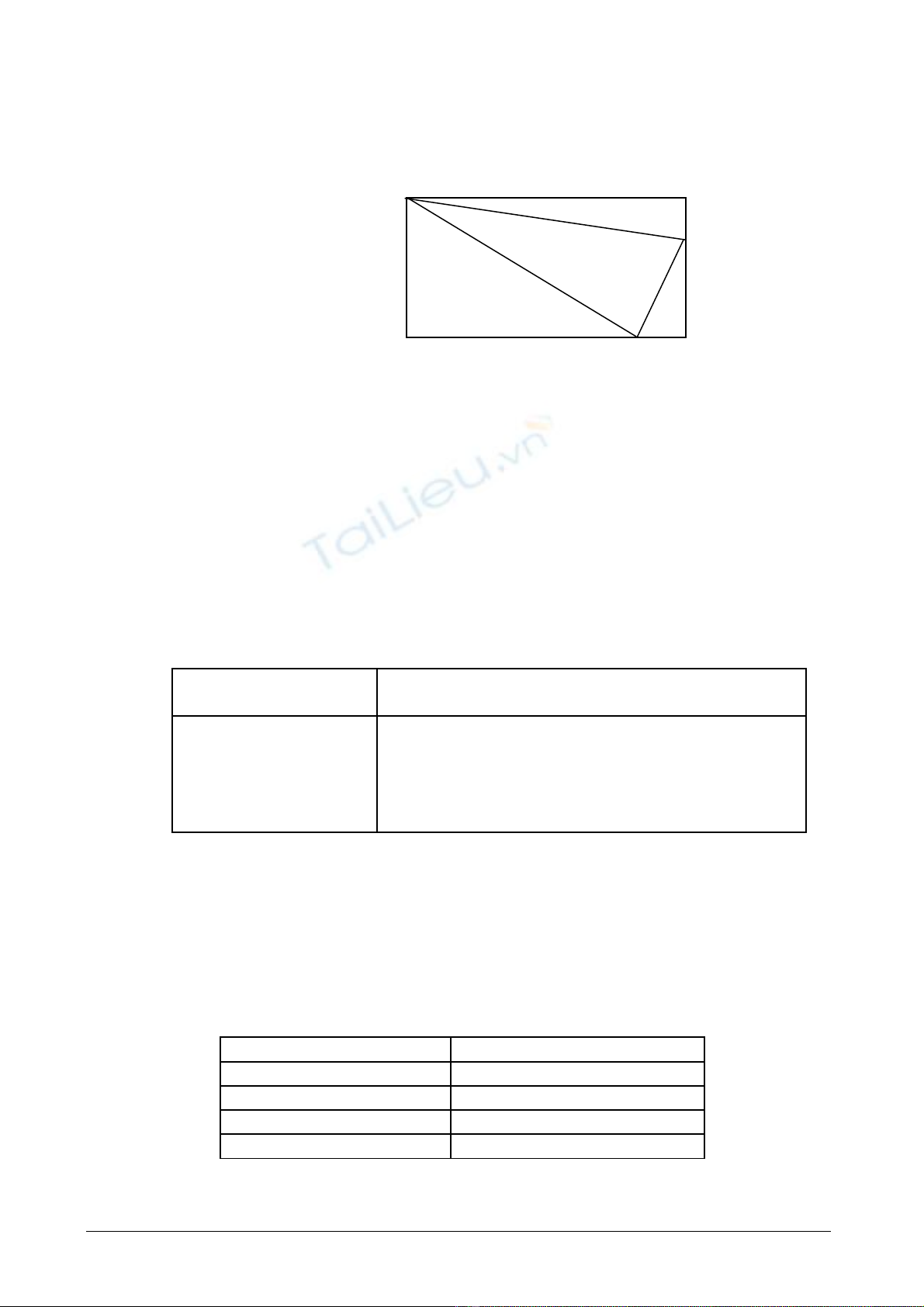
BAØI 11: DIEÄN TÍCH CAÙC HÌNH
Cho hình ch nh t ABCD có chi u dài AB là a (cm), chi u r ng AD là b (cm) v i a, b làữ ậ ề ề ộ ớ
các s nguyên d ng không v t quá 10000. M t đi m M trên đo n BC, m t đi m N trênố ươ ượ ộ ể ạ ộ ể
đo n CD sao cho đ dài (tính b ng cm) các đo n BM, CN b ng nhau và là s nguyên khôngạ ộ ằ ạ ằ ố
âm.
Yêu c u: ầ
1. Bi t đ dài BM, tính di n tích hình ch nh t ABCD và di n tích tam giác MCN.ế ộ ệ ữ ậ ệ
2.Tìm giá tr l n nh t và giá tr nh nh t c a di n tích tam giác AMN khi M, N thay đ i.ị ớ ấ ị ỏ ấ ủ ệ ổ
D li u vào: D li u c a bài toán cho trong t p tin DIENTICH.INP g m ba s a, b, x (xữ ệ ữ ệ ủ ệ ồ ố
≤
b
≤
a, x là đ dài BM trong yêu c u 1) đ c ghi trên cùng m t dòng theo đúng th t trên, haiộ ầ ượ ộ ứ ự
s liên ti p cách nhau m t kho ng tr ng.ố ế ộ ả ắ
D li u ra: K t qu ghi ra màn hình (ho c ghi ra file DIENTICH.OUT) trên 5 dòng:ữ ệ ế ả ặ
- Dòng đ u là ba s a, b và x.ầ ố
- Dòng th hai là di n tích hình ch nh t ABCD.ứ ệ ữ ậ
- Dòng th ba là di n tích tam giác MCNứ ệ
- Dòng th t là giá tr l n nh t c a di n tích tam giác AMNứ ư ị ớ ấ ủ ệ
- Dòng th năm là giá tr nh nh t c a di n tích tam giác AMNứ ị ỏ ấ ủ ệ
(Các giá tr di n tích đ c ghi trong d ng th p phân v i 1 ch s sau d u ph y).ị ệ ượ ạ ậ ớ ữ ố ấ ẩ
Ví d :ụ
DIENTICH.INP K t qu trên màn hình (ho c fileế ả ặ
DIENTICH.OUT)
10 6 2 10 6 2
60.0
4.0
30.0
17.5
H n ch k thu t: ạ ế ỹ ậ
- Ghi tên file bài làm là DIENTICH.PAS.
- D li u vào là chính xác không c n ki m tra.ữ ệ ầ ể
- N u không nh p đ c d li u vào t file, thí sinh có th nh p d li u vào t bàn phímế ậ ượ ữ ệ ừ ể ậ ữ ệ ừ
- Có kho ng 60% s b test có a < 100.ả ố ộ
BAØI 12: ÑOÏC SOÁ LA MAÕ
Vieát chöông trình nhaäp vaøo 1 soá la maõ roài bieán ñoåi thaønh soá thaäp phaân.
Input Output
DCLXVI 666
mmCcXx 2220
MMcmxLIV 2944
mmmcmxcix 3999
Giôùi haïn: Soá La maõ nhaäp vaøo laø chính xaùc. Soá thaäp phaân nhoû hôn 4000.
Gv: Trần Minh Thọ5/5
AB
DC
M
N