www.saosangsong.com.vn Năm học 2009-2010 1
NHÁY A 2006.
Thời gian làm bài : 180 phút
Câu 1 (2 điểm ).
1) Khảo sát biến thiên và vẽ đồ thị (C) của hàm số : y = - 1
3x3 + x2 + 3x - 3.
2) Tìm m để phương trình : |x3| + 3x2 – 9|x| + m = 0 có 4 nghiệm phân biệt .
Câu 2 (2 điểm ) :
1. Giải phương trình :
44 2
4(sin x cos x) + 3(sin x + cosx) - 8 0
22cosx
+
=
−
2. Giải hệ; x x = 1
2(x 1)( 1) x = 2
yy
yy
⎧−+
⎪
⎨++−+
⎪
⎩
Câu 3 (1 điểm ). Tính tích phân /4
22
0
4cos x - 1 x
3cos x - sin x d
π
∫
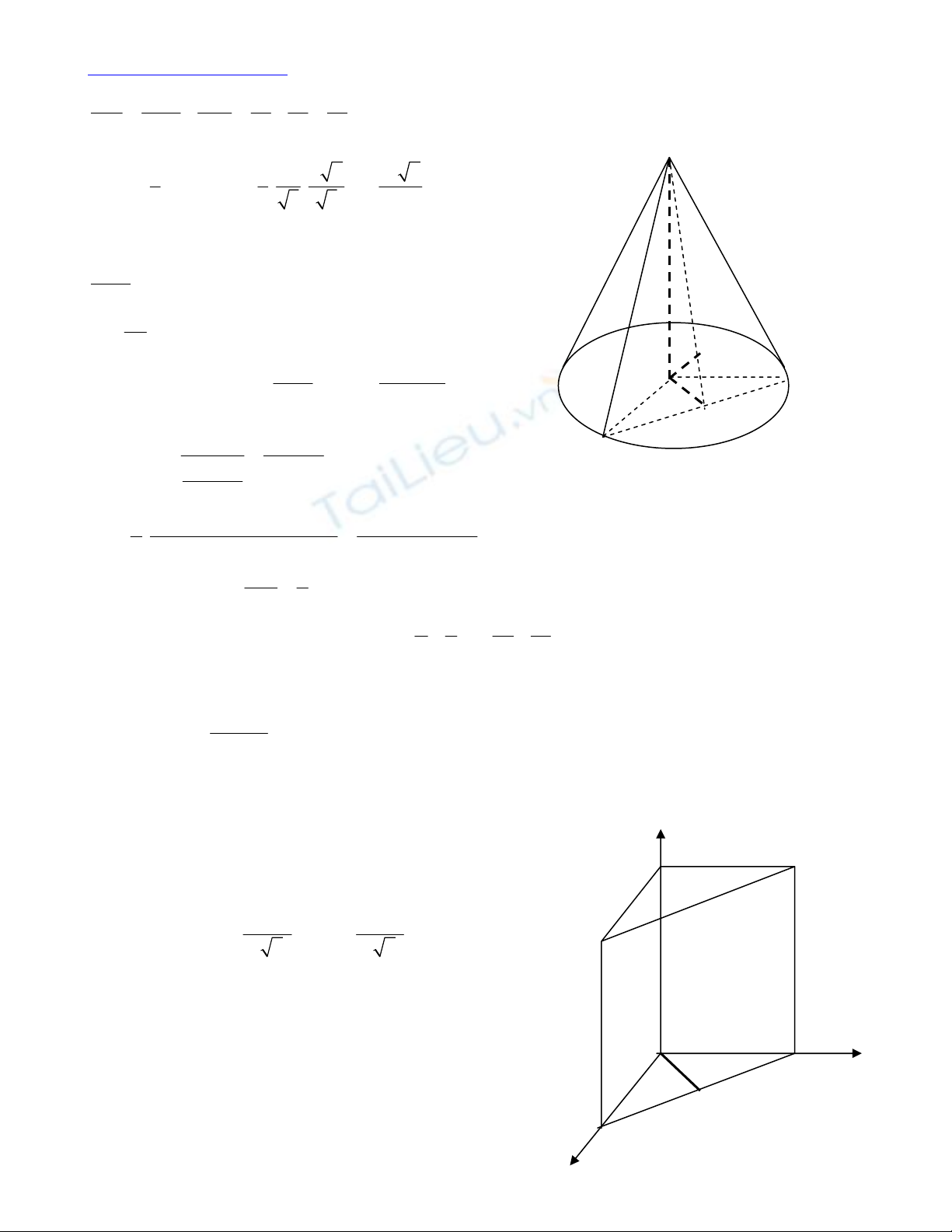
Câu 4 (1 điểm ). Cho hình nón có bán kính đáy và chiều cao đều bằng a. SA và SB là hai đường sinh
của hình nón và nằm trong mặt phẳng cách tâm đáy O một khoảng là a/3. Tính thể tích khối chóp
SABO theo a.
Câu 5 (1 điểm ). Cho hai số x , y thực > 0 và thỏa : xy(x + y) = 2x2 + 2y2. Tìm GTLN của biểu thức :
A = 22
11
xy x
y
+
Câu 6 (2 điểm ).
1. Trong mặt phẳng Oxy, cho tam giác ABC cân tại A biết phương trình AB: 3x – 4y + 1 = 0 và AC:
4x + 3y – 7 = 0 và diện tích của nó là 16. Viết phương trình đường thẳng BC.
2. Trong không gian Oxyz, cho lăng trụ đứng ABC. A’B’C’ có A(0; 0; 0), B(4 ; 0; 0), C(0 ; 4; 0) và
A’(0; 0; 6).
a) Tính khoảng cách giữa BC’ và đường cao AH của đáy.
b) Viết phương trình mặt phẳng qua BC’ và hợp với mặt phẳng (ACC’A’) một góc α mà cosα = 1/3.
Câu 7 (1 điểm ). Cho phương trình : 27 x – 3x + 1 . 6 x - 9.12 x - m. 8x = 0
a) Giải khi m = - 11.
b) Định m để phương trình có 2 nghiệm lớn hơn - 1.
GIẢI VẮN TẮT
Câu 1.
1. y’ = - x2 + 2x + 3 = 0 Ù x = - 1 , x = 3.
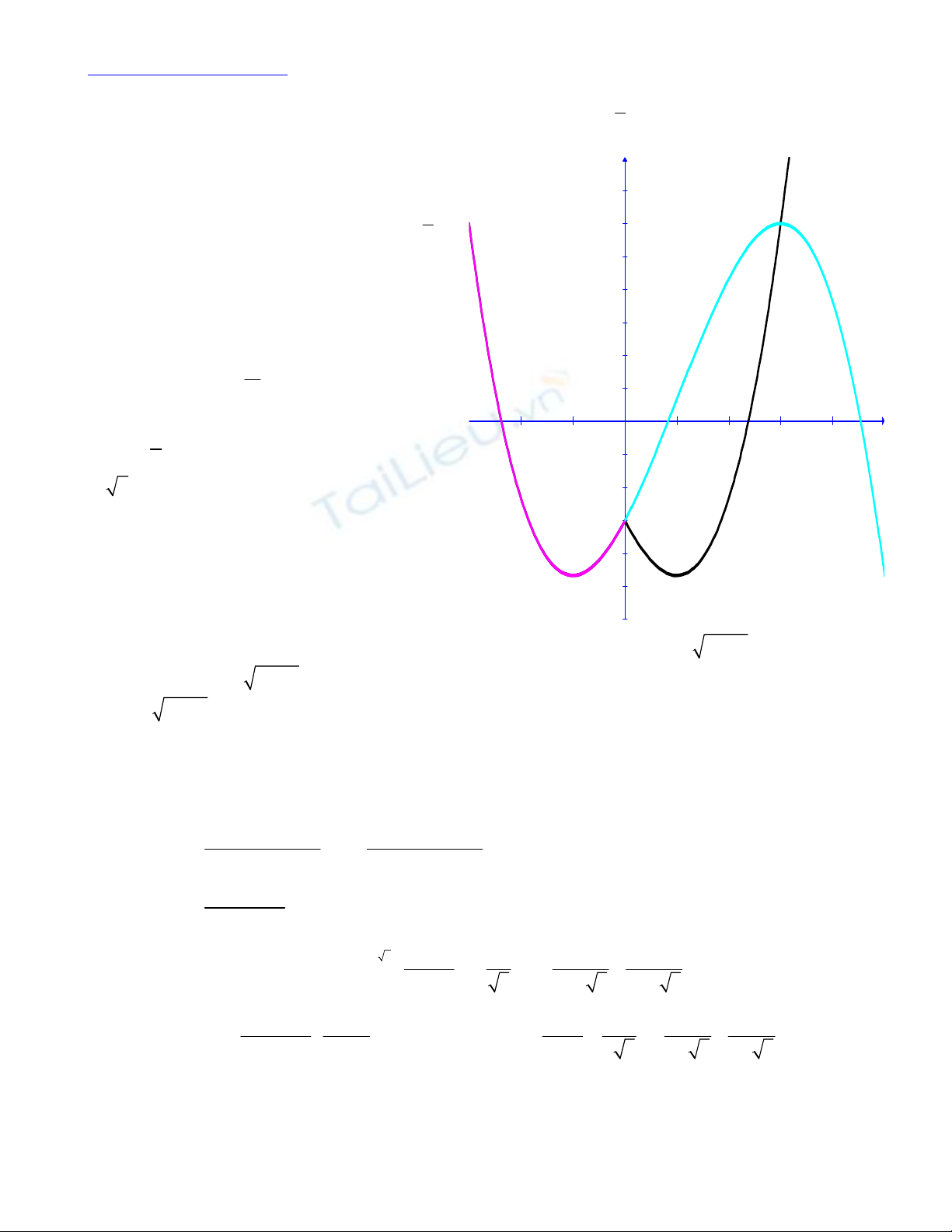
Đồ thị là đoạn màu xanh và màu đỏ.
2. PT Ù 32
1| x| x - 3| x | - 3 = - - 3
33
m
+
www.saosangsong.com.vn Năm học 2009-2010 2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số f(x ) = 32
1| x| x - 3| x | - 3
3+và đường
thẳng y = - m/3 – 3 .
-2 -1 1 2 3 4
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
x
y
Đồ thị hàm số f(x ) gồm hai phần đối xứng qua
Oy vì hàm số này chẵn.
Mặt khác khi x < 0 thì |x | = - x và f(x ) = - 1
3x3
+ x2 + 3x – 3 (cung màu đỏ đã vẽ ở phần 1)
Do đó đồ thị hàm số f(x ) gồm cung màu đỏ và
cung màu đen đối xứng của cung đỏ qua Oy.
Căn cứ vào hình vẽ, đường thẳng y = - m/3 – 3
cắt đồ thị này tại 4 điểm khi
YCBT Ù - 14/3 < - 3
3
m−<−
3
Ù 0 < m < 5
Câu 2.
1. 4(1 - 2
1sin 2x
2) + 3(1 + sin 2x) – 8 = 0 (cosx
≠ 2/2)
Ù 2sin2 2x - 3sin 2x + 1 = 0 Ù sin2x = 1 ,
sin2x = ½
Ù x = π/4 + kπ (chỉ thỏa điều kiện khi k lẻ)
hay x = π/12 + kπ hay x = 5π/12 + kπ (thỏa điều
kiện )
2. Bình phương hai về của phương trình sau: 2x y + 2(x + y) + 2 = x + y + 4 + 4 x y+
Ù 2 xy + (x + y) - 4 x y+ - 2 = 0 (*)
Đặt t = x y+≥ 0 , từ phương trình đầu: xy = t + 1. Thế vào (*) :
Ù 2( t + 1) + t2 - 4t – 2 = 0 Ù 220tt−=
Ù t = 0 hay t = 2 .
Vậy (x + y = 0 và xy = 1 ) hay ( x + y = 4 và x y = 3)
Ù (x = 3; y = 1) hay (x = 1; y = 3)
Câu 3. /4 /4
22 22
00
4cos
3cos sin 3cos sin
xdx dx
I
JK
x
xxx
ππ
=−=
−−
∫∫ −
Tính J: J = /4
2
0
4cos
34sin
x
dx
x
π
−
∫
Đặt t = sin x => dt = cosxdx => J = 2/2 /4
2
00
211
434 32323
dt dt
ttt
π
⎛⎞
=− −
⎜⎟
−−+
⎝⎠
∫∫
Tính K: : K = /4
2
0
1
3 tan cos
dt
2
x
x
π
⎛⎞
⎜⎟
−
⎝⎠
∫ . Đặt t = tanx : K = 11
2
00
111
323 3 3
dt dt
ttt
⎛⎞
=−
⎜⎟
−−+
⎝⎠
∫∫
Câu 4: Gọi I là trung điểm của AB, kẻ OH vuông góc SI thì OH = a/3.
www.saosangsong.com.vn Năm học 2009-2010 3
2 2 2222
11191
OI OH OS a a a
=−=−=
8
=> OI2 = a2 /8.
=> AI2 = OA2 – OI2 = 7a2 /8.
=> V =
3
117
... . . .
33
88
aa a
OI AI SO a==
7
24
Câu 5: Đặt S = x + y, P = x y : SP = 2(S2 – 2P) Ù P =
2
2
4
S
S+
A = 2
S
P
Đk : S2 – 4P ≥ 0 Ù S2 -
23
84
00
44
SSS
SS
−
≥ <=> ≥
++
S
A
B
O
H
I
2
Ù S ≥ 4 vì S > 0 .
A = S /P2 =
2
43
2
(4)
44
(4)
SS
SS
S
+
=
+
A’ =
322
64
1 2( 4) ( 4) .3 ( 4)( 12)
.0
44
SSS S S S
SS
+−+ +−−
=<=> A nghịch biến.
Vậy max A = f(4) =
2
3
8
4.4 4
=1
Ù S = 4 và P = 4 Ù x = y = 2
Cách khác : Chia hai vế x2y2 , giả thiết
Ù
22
11 1 1
2( )
xyx
+= +
Đạt a = 1/x, b = 1/y, ta được : a + b = 2(a2+ b2)
Mà a2+ b2 ≥ (a+ b)2/2 nên giả thiết cho ta: a + b ≥ (a + b)2=> a + b ≤ 1 vì a + b > 0
A =
3
()
() 4
ab
ab vì ab ≤ (a + b)a b +
+≤ 2/4, suy ra A ≤ ¼. Vậy maxA = ¼ khi a = b = ½
Ù
x = y = 2.
Câu 6.
1. AB : 3x – 4y + 1 = 0 , AC: 4x + 3y – 7 = 0
Suy ra A = (1 ; 1) và góc A = 900. Phương trình BC song song với các phân giác của AB, AC cho bởi :
3x 4 1 4x 3 7 0 3x 4 1 4x -3 7 0y y hay y y−++ +−= −+− +=
A
B
C
A’
B’
C’
H
=> BC: 7x – y + c = 0 hay x + 7y + c = 0
Vì tam giác ABC vuông cân nên diện tích nó bằng : AH2 =
16 ( H là chân đường cao) => AH = 4.
Ù d(A, BC) = 4 Ù |6 | |8 |
44
52 52
cc
hay
++
==
Suy ra c và phương trình đường thẳng BC.
2. a) C’ (0; 4; 6) => ;
' ( 4; 4; 6) ; (2; 2; 0)BC AH=− =
JJJJG JJJG
(0; 4;0)AB =
JJJG
=> [ ', ] ( 12;12 ; 16)BC AH =− −
JJJJGJJJG
=> ['
, ]. 4BC AH AB =
JJJJG JJJG JJJG
8
www.saosangsong.com.vn Năm học 2009-2010 4
=> d(BC’, AH) = 222
48 12
34
12 12 16
=
++
b) (ACC’A’): x = 0
PT (P) cần tìm : ax + by + cz – 4a = 0 vì qua B(4; 0; 0).
Ta có : 4b + 6c – 4a = 0 Ù 2a – 2b – 3c = 0 vì (P) qua C’(0 ; 4; 6).
Ta có : 222
|| 1
cos 3
a
abc
α
==
++
Thế b = (2a – 3c)/2 : 9a2 = a2 + (2a – 3c)2/4 + c2
Ù 36a2 = 4 a2 + 4 a2 – 12ac + 9 c2 + 4c2 Ù 13c2 - 12ac – 28 a2 = 0
Ù c = 2a hay c = - 14a/13
Vậy (P): x – 2y – 2z – 4 = 0 hay . . .
Câu 7. Chia hai vế cho 8x : (3/2) 3x – 3.(3/2)2 x - 9.(3/2) x - m = 0 .
a) m = - 11 : t3 – 3t2 - 9t + 11 = 0 Ù ( t – 1)(t2 – 2t – 11) = 0 với t = (3/2)x > 0
Ù t = 1 hay t = 1 + 2 3 Ù x = log3/2 2 hay x = log3/2 (1 + 2 3)
b) f(t) = t3 – 3t2 - 9t = m
x > - 1 => t > 2/3.
Khảo sát : f’(t) = 3t2 – 6t – 9 = 0 Ù t = 3.
Hàm số có giá trị nhỏ nhất là f(3) = - 27 .
Và f(2/3) = - 190/27 . Căn cứ vào BBT, phương trình có 2 nghiệm > - 1 khi – 27 < m < - 190/27.