Báo cáo khoa học: "nghiên cứu ảnh h-ởng của bề dày lớp bêtông nhựa tới các đặc tính nhiệt bên trong các lớp mặt cầu bêtông"

Chia sẻ: Nguyễn Phương Hà Linh Nguyễn Phương Hà Linh | Ngày: | Loại File: PDF | Số trang:9

Thêm vào BST

Báo xấu

54
lượt xem 8
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bề dày lớp bêtông nhựa (BTN) trải trên mặt cầu bêtông là thông số có ảnh h-ởng tới độ bền sử dụng và chi phí trong xây dựng. Về ph-ơng diện nhiệt, do nằm phía trên nên lớp BTN là bộ phận gánh chịu trực tiếp và phần lớn tác động bất lợi của các yếu tố thời tiết nh- nắng, m-a, thay đổi nhiệt độ không khí...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Báo cáo khoa học: "nghiên cứu ảnh h-ởng của bề dày lớp bêtông nhựa tới các đặc tính nhiệt bên trong các lớp mặt cầu bêtông"

nghiªn cøu ¶nh h−ëng cña bÒ dμy líp bªt«ng nhùa tíi c¸c ®Æc tÝnh nhiÖt bªn trong c¸c líp mÆt cÇu bªt«ng PGS. TS. TrÞnh V¨n Quang ThS. NguyÔn M¹nh Hïng Khoa C¬ khÝ - §HGT Tãm t¾t: Bμi b¸o tr×nh bμy ph−¬ng ph¸p ®¸nh gi¸ ¶nh h−ëng cña ®é dμy líp bªt«ng nhùa trªn mÆt cÇu tíi tr¹ng th¸i nhiÖt cña c¸c líp trong mÆt cÇu. Summary: The paper presents the method of estimating the influences of the asphalt thickness on temperture state of interior layers of concrete bridge surface. I. §Æt vÊn ®Ò BÒ dµy líp bªt«ng nhùa (BTN) tr¶i trªn mÆt cÇu bªt«ng lµ th«ng sè cã ¶nh h−ëng tíi ®é bÒn sö dông vµ chi phÝ trong x©y dùng. VÒ ph−¬ng diÖn nhiÖt, do n»m phÝa trªn nªn líp BTN lµ bé phËn g¸nh chÞu trùc tiÕp vµ phÇn lín t¸c ®éng bÊt lîi cña c¸c yÕu tè thêi tiÕt nh− n¾ng, m−a, thay ®æi nhiÖt ®é kh«ng khÝ... MÆt kh¸c líp nhùa cã tÝnh chÊt nhiÖt kh¸c víi líp bªt«ng phÝa d−íi, bëi vËy vÊn ®Ò ®Æt ra lµ sù thay ®æi bÒ dµy líp BTN cã ¶nh h−ëng ®Õn c¸c tr¹ng th¸i nhiÖt cña c¸c líp bªn trong mÆt cÇu nh− thÕ nµo trong cïng c¸c ®iÒu kiÖn n¾ng, m−a vµ thay ®æi nhiÖt ®é kh«ng khÝ. II. Ph−¬ng ph¸p kh¶o s¸t ®¸nh gi¸ 1. Chän d÷ liÖu ban ®Çu Th«ng th−êng bÒ dµy mÆt cÇu nhá h¬n nhiÒu so víi bÒ réng cña mÆt cÇu. Gi¶ ®Þnh mét mÆt cÇu bªt«ng cã bÒ réng bC = 12 m, bÒ dµy hC = 0,21 m. BÒ dµy mÆt cÇu gåm 2 líp: hC = h 1 + h 2; víi h1 lµ bÒ dÇy líp bªt«ng nhùa, h2 lµ bÒ dµy líp bªt«ng. Do bÒ dµy mÆt cÇu hC nhá h¬n rÊt nhiÒu bÒ réng bC: hC
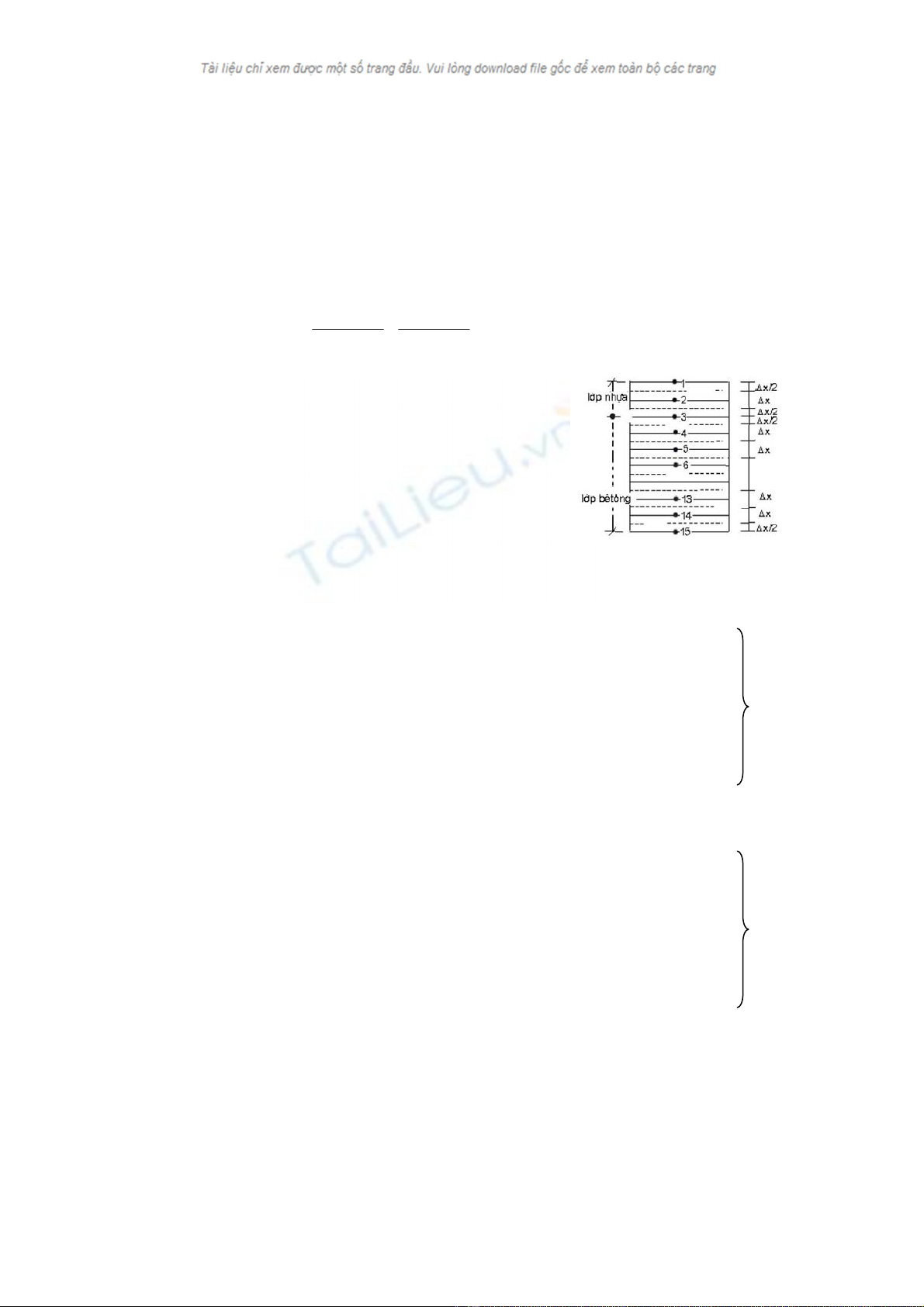
2. Ph−¬ng ph¸p kh¶o s¸t a. X¸c ®Þnh nhiÖt ®é t¹i c¸c vÞ trÝ trong mÆt cÇu Chia bÒ dµy mÆt cÇu lµm 14 kho¶ng c¸ch ®Òu cã Δx = 0,21m/14 = 0,015 m (h×nh 1). C¸c ®iÓm cÇn x¸c ®Þnh nhiÖt ®é lµ: i = 1, 2, 3..., 15 nh− h×nh 2. B−íc thêi gian kh¶o s¸t khi trêi n¾ng Δτ = 3600 s; khi trêi m−a Δτ = 120 s (cã sè b−íc p = 1, 2, 3...). Trªn mçi phÇn tö giíi h¹n lµ c¸c ®−êng nÐt ®øt cã ®é t¨ng néi n¨ng b»ng tæng l−îng nhiÖt ®Õn tõ hai phÝa sau thêi gian Δτ: ⎡ (tP +1 − tP +1) (tP +1 − tP +1) ⎤ P +! ⎢ i −1 + i +1 ⎥.Δτ = Ci .(t i − ti ) P i i (1) ⎢ ⎥ Ri −1 Ri+1 ⎣ ⎦ Trong ®ã R0 vµ R16 = 1/α (i = 1vµ i = 15) lµ nhiÖt trë to¶ nhiÖt; α hÖ sè to¶ nhiÖt; Ri ± 1 = δi/λi. Δx lµ nhiÖt trë dÉn nhiªt; Ci = ci.ρiΔVi lµ nhiÖt dung khèi cña phÇn tö thuéc ®iÓm i. t16P+1 = tKP+1 (i = 15) lµ nhiÖt ®é kh«ng khÝ (b¶ng 1); δi, ΔVi bÒ dµy vµ thÓ tÝch phÇn tö kh¶o s¸t i; ci - nhiÖt dung riªng; ρi - khèi l−îng riªng cña vËt liÖu. Khi trêi n¾ng: t0P+1 = tΣKP+1 (i = 1) lµ nhiÖt ®é t−¬ng ®−¬ng kh«ng khÝ cã kÓ bøc x¹ mÆt trêi khi trêi n¾ng: t p +1 = t p +1 + ΣK K H×nh 1. S¬ ®å chia c¸c phÇn tö ε.IP+1/α.I; I theo b¶ng 1; ε = 0,75 lµ hÖ sè hÊp thô tia mÆt trêi x¸c ®Þnh nhiÖt ®é cña mÆt cÇu; α = 7,89 W/m2®é, x¸c ®Þnh theo ph−¬ng tr×nh tiªu chuÈn to¶ nhiÖt Nu = 0,032Re0,8. Tõ ®ã lËp ®−îc hÖ ph−¬ng tr×nh: 14,4255t1 P +1 - 11,4792.t2 P+1 = t1 P + 1,9463.tΣKP+1 - §iÓm 1: -5,73953.ti-1 P +1 + 12,47960.ti P +1 - 5,73953.ti+1 P +1 = ti P - C¸c ®iÓm thuéc líp BTN: - §iÓm tiÕp gi¸p (2) -5,7702.ti-1 P +1 + 21,6504.ti P +1 - 14,08802.ti+1 P +1 = ti P gi÷a líp BTN vµ bªt«ng: -14,9602.ti-1 P +1 + 30,9204.ti P +1 - 14,9602.ti+1 P +1 = ti P - C¸c ®iÓm thuéc líp bªt«ng: -29,9205t14 P +1 + 32,8877.t15 P+1 = t15 P + 1,9672.tKP+1 - §iÓm 15: Khi trêi m−a: t0P+1 = tΣKP+1 = 25 0C = const (i = 1) lµ nhiÖt ®é n−íc m−a; α = 252,8 W/m2®é tÝnh theo ph−¬ng tr×nh tiªu chuÈn NuL = 0,037.ReL0,3.Pr0,43.(Prl /Prm )0,25. Tõ ®ã lËp ®−îc hÖ ph−¬ng tr×nh: 3,4621.t1 P +1 - 0,3891.t2 P+1 = t1 P + 51,95 - §iÓm 1: - 0,1913.ti-1 P +1 + 1,3826.ti P +1 - 0,1913.ti+1 P +1 = ti P - C¸c ®iÓm thuéc líp BTN: - §iÓm tiÕp gi¸p gi÷a (3) - 0,19233.ti-1 P +1 + 1,6883.ti P +1 - 0,496.ti+1 P +1 = ti P líp BTN vµ bªt«ng: - 0,4986.ti-1 P +1 + 1,9972.ti P +1 - 0,4986.ti+1 P +1 = ti P - C¸c ®iÓm thuéc líp bªt«ng: - 0,9973.t14 P +1 + 2,06287.t15 P+1 = t15 P + 0,06557.tKP+1 - §iÓm 15: Mçi hÖ (2), (3) trªn gåm 15 ph−¬ng tr×nh tuyÕn tÝnh, chøa 15 nghiÖm ph¶i t×m lµ c¸c nhiÖt ®é tp +1 , viÕt d¹ng ma trËn vµ gi¶i b»ng ph−¬ng ph¸p ma trËn nghÞch ®¶o: i [ aij ]*[ti] = [Ci] → [ti] = [ aij ]-1 * [Ci] (4)
b. X¸c ®Þnh miÒn bÞ kÐo vμ nÐn trong bÒ dμy mÆt cÇu Theo lý thuyÕt biÕn d¹ng nhiÖt [1], viÖc x¸c ®Þnh miÒn bÞ kÐo hoÆc bÞ nÐn ph¶i c¨n cø vµo ®é chªnh trung b×nh ΔtTBP gi÷a nhiÖt ®é trung b×nh tuyÕn tÝnh tTBP(x) vµ nhiÖt ®é thùc tP(x) ë tõng thêi ®iÓm t¹i mçi vÞ trÝ trong mÆt cÇu: ΔtTBP = tTBP(x) - tP(x) (5) P trong ®ã nhiÖt ®é trung b×nh tuyÕn tÝnh t (x) x¸c ®Þnh theo: TB x tP ( x ) = t p − ( t p − t p ) (6) TB δ A A B ⎛ eP ⎞ ⎛ ⎞ SP SP P ⎜2 − 3 e ⎜3 − 1⎟ ⎟; t m = 2. t P = 2. víi: (7) ⎜ ⎟ ⎜δ ⎟ A B δ δ δ ⎝ ⎠ ⎝ ⎠ δ lµ bÒ dµy mÆt cÇu; x to¹ ®é; tAP vµ tBP lµ trÞ sè nhiÖt ®é trung b×nh tuyÕn tÝnh t¹i hai mÆt mÆt cÇu; SP vµ eP lµ diÖn tÝch vµ träng t©m miÒn bÞ kÐo t¹i mçi thêi ®iÓm p. MiÒn bÞ kÐo cã: ΔtTBP > 0. MiÒn bÞ nÐn cã: ΔtTBP < 0. IiI. KÕt qu¶ tÝnh to¸n vμ c¸c nhËn xÐt 1. Tr¹ng th¸i nhiÖt khi trêi n¾ng HÖ (2) ®−îc gi¶i theo ph−¬ng ph¸p (4) lÇn l−ît víi c¸c tr−êng hîp bÒ dµy líp BTN dµy: 3 cm; 4,5 cm; 6 cm; 7,5 cm. KÕt qu¶ tÝnh to¸n ®−îc ph©n bè nhiÖt ®é trong bÒ dµy mÆt cÇu t¹i 24 giê trong ngµy vµ ®é chªnh nhiÖt ®é trung b×nh ®−îc thÓ hiÖn trªn c¸c h×nh 2, 3, 4, 5, 6, 7, 8, 9. 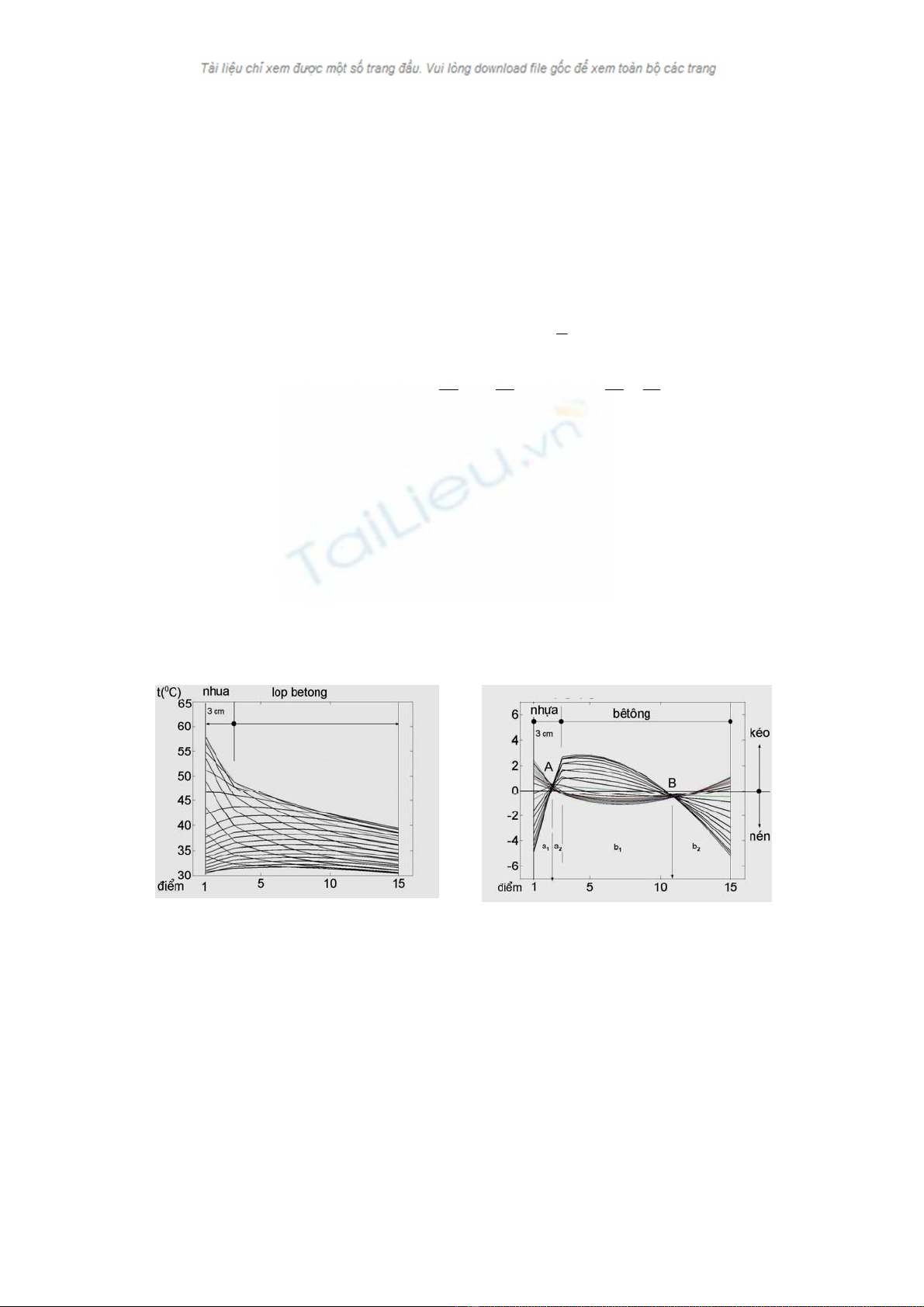H×nh 2. Ph©n bè nhiÖt ®é trong bÒ dμy mÆt cÇu cã H×nh 3. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã líp BTN dμy 3 cm vμo ngμy n¾ng líp BTN dμy 3 cm vμo ngμy n¾ng NhËn xÐt: C¸c ®Æc tÝnh nhiÖt chung ++ Ph©n bè nhiÖt ®é t¹i c¸c vÞ trÝ trong mÆt cÇu theo tõng thêi giê trong ngµy thÓ hiÖn trªn c¸c ®å thÞ h×nh 2, 4, 6, 8. Tõ c¸c h×nh nµy cã thÓ thÊy c¸c quy luËt chung sau: - C¸c ®−êng cong lâm (chiÒu lâm quay lªn trªn) biÓu thÞ nhiÖt ®é trong mÆt cÇu khi nhËn nhiÖt vµo buæi s¸ng (6-13h), c¸c ®−êng cong låi lµ nhiÖt ®é buæi chiÒu (sau 13h). C¸c ®−êng cong lâm lu«n tån t¹i ®iÓm gÉy khóc ë chç tiÕp gi¸p gi÷a líp nhùa vµ bªt«ng.
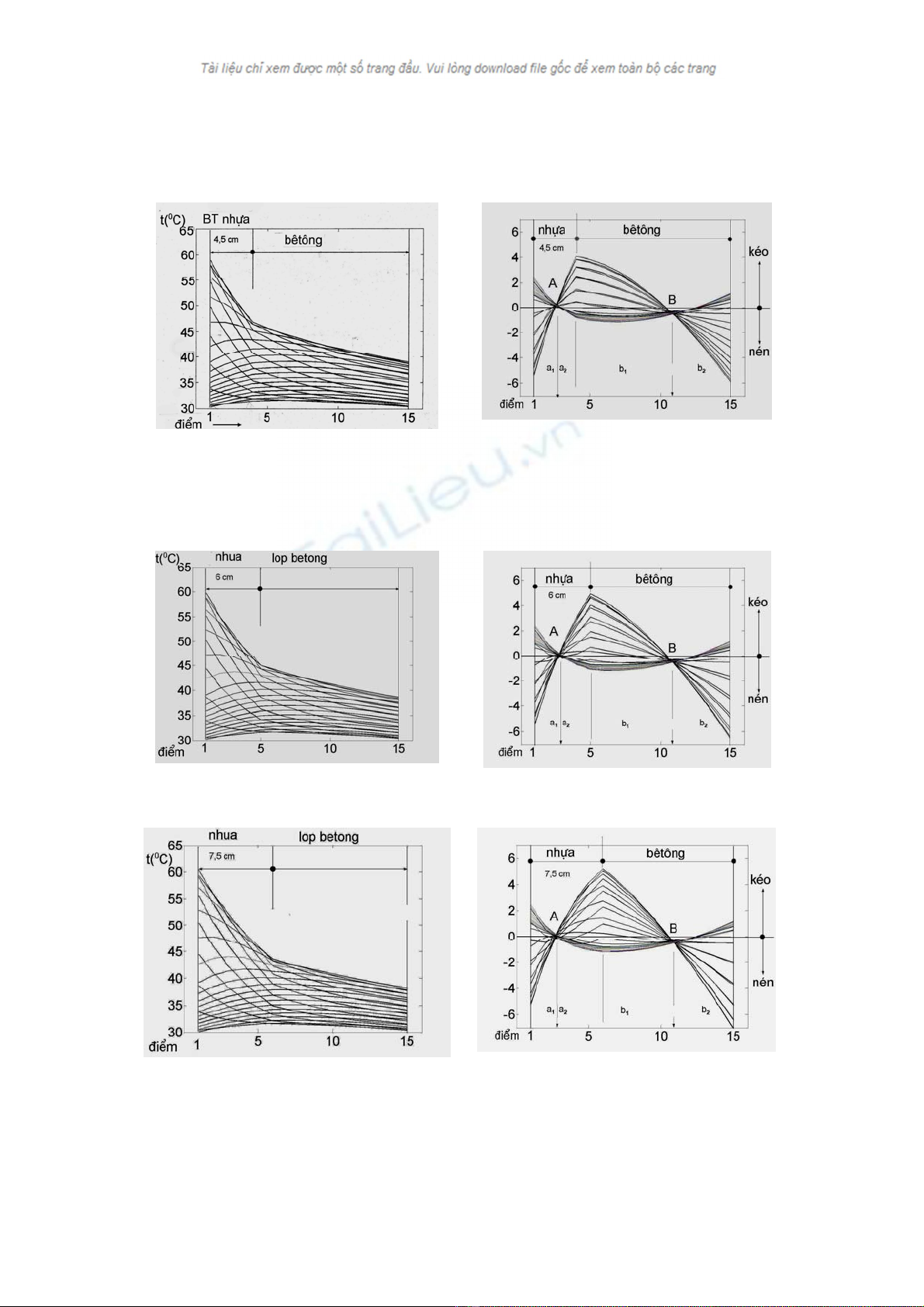
- §é dèc ®−êng cong lâm lu«n lín h¬n ®−êng cong låi vµ ë trong líp BTN lu«n lín h¬n trong líp bªt«ng. §é dèc ®−êng nhiÖt ®é chÝnh lµ gradien nhiÖt ®é, cã gi¸ trÞ lín nhÊt vµo 11h. H×nh 4. Ph©n bè nhiÖt ®é trong bÒ dμy mÆt cÇu cã H×nh 5. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã líp BTN dμy 4,5 cm vμo ngμy n¾ng líp BTN dμy 4,5 cm vμo ngμy n¾ng ++ HiÖu sè gi÷a nhiÖt ®é trung b×nh tuyÕn tÝnh vµ nhiÖt ®é thùc t−¬ng øng: ΔtTBP = tTBP(x) - tP(x) biÓu thÞ møc ®é kÐo nÐn ®−îc thÓ hiÖn trªn c¸c ®å thÞ h×nh 3, 5, 7, 9. Tõ c¸c ®å thÞ cã thÓ thÊy c¸c quy luËt chung sau: H×nh 6. Ph©n bè nhiÖt ®é trong bÒ dμy mÆt cÇu cã H×nh 7. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã líp BTN dμy 6 cm vμo ngμy n¾ng líp BTN dμy 6 cm vμo ngμy n¾ng H×nh 9. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã H×nh 8. Ph©n bè nhiÖt ®é trong bÒ dμy mÆt cÇu cã líp BTN dμy 7,5 cm vμo ngμy n¾ng líp BTN dμy 7,5 cm vμo ngμy n¾ng
- T¹i mçi thêi ®iÓm trong líp mÆt cÇu lu«n tån t¹i hai ®iÓm A vµ B lµ ®iÓm ph©n chia bÒ dµy mÆt cÇu thµnh 4 miÒn: líp BTN cã 2 miÒn a1, a2; líp bªt«ng 2 miÒn b1; b2. - C¸c miÒn kÐo nÐn trong mçi vËt liÖu cã ®Æc tÝnh kÐo nÐn ng−îc chiÒu nhau vµ lu©n phiªn nhau, vµ ®Æc biÖt tû lÖ víi nhau nghÜa lµ a1 bÞ kÐo m¹nh th× a2 bÞ nÐn m¹nh vµ ng−îc l¹i; b1 vµ b2 còng t−¬ng tù. - §Æc tÝnh kÐo nÐn cña miÒn a1 vµ b2 gièng nhau, miÒn a2 vµ b1 gièng nhau. Nh− vËy A B nh− lµ 2 ®iÓm tùa cña c¸c ®ßn b¶y cña lùc kÐo nÐn, hay nãi c¸ch kh¸c c¸c qu¸ tr×nh nhiÖt dao ®éng cña mÆt trªn lu«n cã ¶nh h−ëng vµ còng bÞ phô thuéc vµo mÆt phÝa d−íi. §©y lµ ®Æc ®iÓm næi bËt cña vËt liÖu trong chÕ ®é truyÒn nhiÖt dao ®éng. - A, B lµ ®iÓm x¸c ®Þnh bÒ dµy cña miÒn bÞ kÐo vµ bÞ nÐn cña mçi líp BTN vµ bªt«ng. ¶nh h−ëng cña bÒ dµy líp nhùa - Khi bÒ dµy líp BTN t¨ng, ®iÓm B kh«ng thay ®æi, ®iÓm A dÞch chuyÓn s©u vµo phÝa trong, vµ bÒ dµy miÒn a2 t¨ng nhanh. t1 +1 − tP +1 P - MËt ®é dßng nhiÖt t¹i bÒ mÆt x¸c ®Þnh bëi: q = - λ.gradt ≈ λ1. 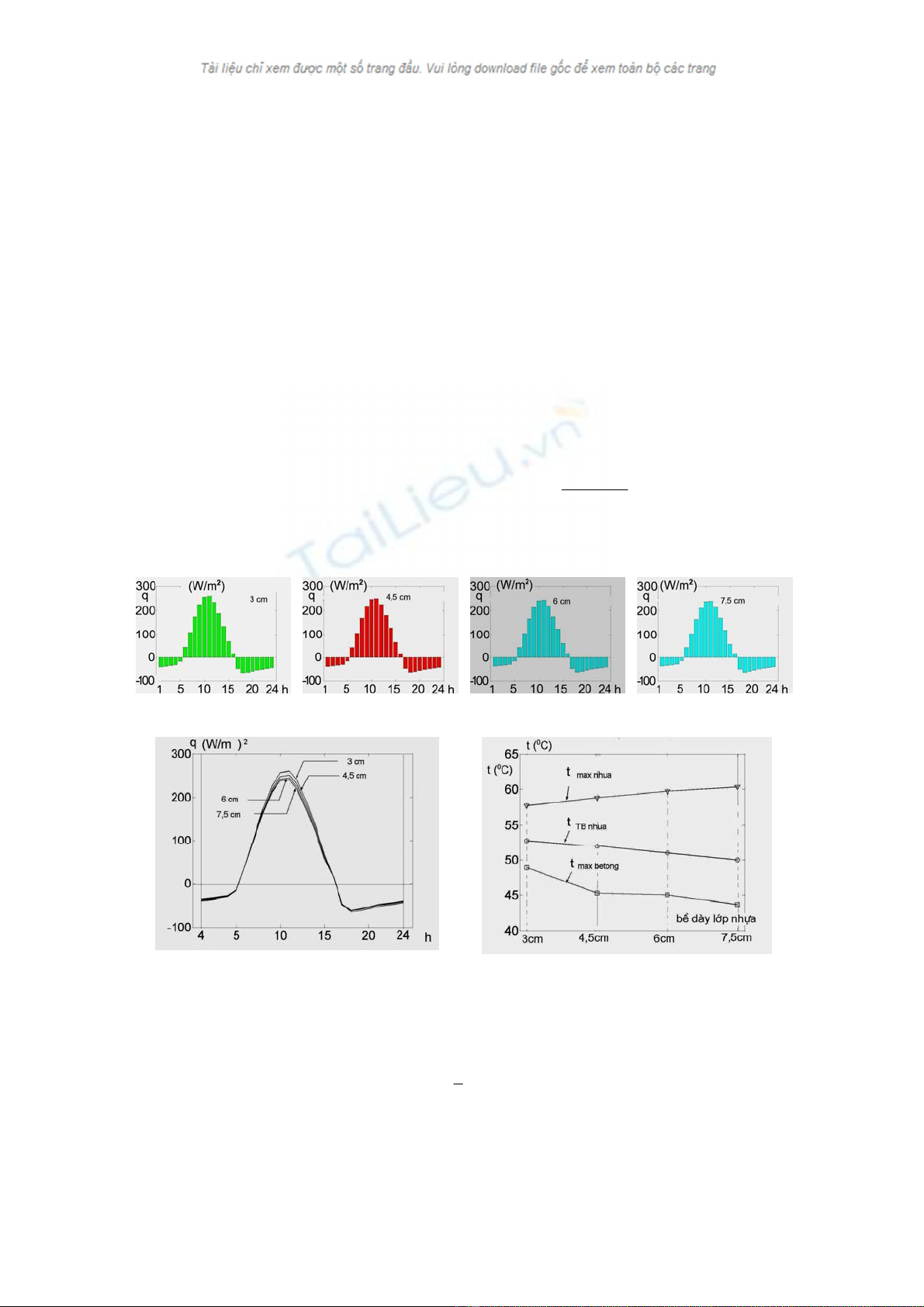Dßng nhiÖt q øng víi 2 Δx líp BTN cã bÒ dµy kh¸c nhau ®−îc thÓ hiÖn trªn h×nh 10 a, b, c, d. So s¸nh q thÊy r»ng kh¸c nhau kh«ng ®¸ng kÓ: khi bÒ dµy líp BTN t¨ng, q gi¶m chØ vµo c¸c giê 10h, 11h, 12h, 13h: q(3cm) ≥ q(4,5cm) ≥ q(6cm) ≥ q(7,5cm); c¸c giê kh¸c coi lµ q b»ng nhau (h×nh 11). H×nh 10 a H×nh 10 b H×nh 10 c H×nh 10 d H×nh 12. NhiÖt ®é cùc ®¹i t¹i mÆt trªn líp BTN vμ H×nh 11. MËt ®é dßng nhiÖt t¹i bÒ mÆt cÇu theo giê mÆt trªn líp bªt«ng, nhiÖt ®é trung b×nh cña líp nhùa trong ngμy øng víi bÒ dμy líp BTN kh¸c nhau phô thuéc vμo bÒ dμy líp nhùa Tõ h×nh 12 cã thÓ thÊy, khi bÒ dµy líp BTN t¨ng: - NhiÖt ®é cùc ®¹i t¹i mÆt trªn líp BTN tmax nhua cµng cao; n ∑t 1 - NhiÖt ®é trung b×nh cña líp nhùa t TB.nhua = gi¶m; i n i =1
- NhiÖt ®é cùc ®¹i t¹i mÆt trªn líp bªt«ng tmax.betong gi¶m H×nh 14. Møc ®é bÞ kÐo vμ nÐn lín nhÊt ®ång thêi x¶y H×nh 13. Møc ®é bÞ kÐo vμ nÐn lín nhÊt ®ång thêi x¶y ra lóc 10h t¹i hai mÆt trªn vμ d−íi líp BTN phô thuéc ra lóc 17h t¹i hai mÆt trªn vμ d−íi líp BTN phô thuéc vμo bÒ dμy líp nhùa vμo bÒ dμy líp nhùa Møc ®é kÐo nÐn lín nhÊt t¹i mÆt trªn vµ mÆt d−íi cña líp BTN ®−îc x¸c ®Þnh vµo 10h vµ 17h, thÓ hiÖn nh− sau: - Tõ h×nh 13 cho thÊy mÆt trªn líp BTN bÞ kÐo rÊt m¹nh lóc 17h do to¶ nhiÖt ra bªn ngoµi lµm nhiÖt ®é gi¶m nhanh; mÆt d−íi líp nhùa bÞ nÐn víi møc ®é nhá. Khi bÒ dµy líp nhùa t¨ng møc ®é bÞ kÐo cña mÆt trªn gÇn nh− kh«ng thay ®æi, møc ®é bÞ nÐn t¹i mÆt d−íi gi¶m chót Ýt. - Tõ h×nh 14 cho thÊy lóc 10h t¹i mÆt trªn líp nhùa do nhËn nhiÖt bøc x¹ mÆt trêi nhiÖt ®é t¨ng gi·n në nhiÒu nªn bÞ nÐn m¹nh; ph¶n øng cña mÆt d−íi líp nhùa l¹i bÞ kÐo rÊt m¹nh vµ lín nhÊt. Khi bÒ dµy líp nhùa t¨ng møc ®é bÞ kÐo cña mÆt d−íi líp nhùa t¨ng, møc ®é bÞ nÐn t¹i mÆt trªn líp nhùa thay ®æi kh«ng ®¸ng kÓ. 2. Tr¹ng th¸i nhiÖt khi gÆp m−a Tr¹ng th¸i nhiÖt khi gÆp m−a ®−îc kh¶o s¸t vµo thêi ®iÓm m−a lµ 12h. §ã lµ thêi ®iÓm nhiÖt ®é bÒ mÆt ®¹t gi¸ trÞ cao nhÊt nªn khi gÆp m−a sÏ g©y biÕn ®æi tr¹ng th¸i bÊt lîi nhÊt ®èi víi mÆt cÇu. NhËn xÐt c¸c ®Æc tÝnh chung ++ Ph©n bè nhiÖt ®é trong mÆt cÇu vµ ®−êng nhiÖt ®é trung b×nh tuyÕn tÝnh thay ®æi theo tõng thêi ®iÓm sau m−a thÓ hiÖn trªn c¸c ®å thÞ h×nh 15, 17, 19, 21. Tõ c¸c h×nh nµy cã thÓ thÊy c¸c quy luËt chung sau: H×nh 15. §−êng cong nhiÖt ®é vμ ®−êng nhiÖt ®é H×nh 16. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã trung b×nh tuyÕn tÝnh sau m−a trong mÆt cÇu cã líp líp BTN dμy 3 cm sau m−a 12h tr−a BTN dμy 3 cm
H×nh 17. §−êng cong nhiÖt ®é vμ ®−êng nhiÖt ®é H×nh 18. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã trung b×nh tuyÕn tÝnh sau m−a trong mÆt cÇu cã líp líp BTN dμy 4,5 cm sau m−a 12h tr−a BTN dμy 4,5 cm - Ngay sau khi gÆp n−íc m−a cã nhiÖt ®é thÊp nhiÖt ®é líp nhùa phÝa trªn mÆt gi¶m rÊt nhanh vµ líp nhùa máng trªn mÆt bÞ kÐo rÊt m¹nh. BÒ dµy miÒn bÞ kÐo x¸c ®Þnh bëi to¹ ®é cña ®iÓm giao gi÷a ®−êng cong nhiÖt ®é thùc vµ ®−êng nhiÖt ®é trung b×nh tuyÕn tÝnh t−¬ng øng. Sau ®ã møc ®é bÞ kÐo gi¶m dÇn ®ång thêi bÒ dµy miÒn bÞ kÐo cña líp nhùa t¨ng dÇn. C¸c giao ®iÓm trªn dÇn tiÕn tíi ®iÓm giíi h¹n lµ ®iÓm A, nghÜa lµ bÒ dµy miÒn bÞ kÐo trong líp nhùa chØ tiÕn ®Õn giíi h¹n nhÊt ®Þnh. - Theo thêi gian sau m−a c¸c ®−êng nhiÖt ®é trung b×nh tuyÕn tÝnh chØ quay quanh 1 ®iÓm cè ®Þnh: ®iÓm B. C¸c ®−êng cong nhiÖt ®é thùc c¾t c¸c ®−êng ®−êng nhiÖt ®é trung b×nh tuyÕn tÝnh t−¬ng øng t¹i hai ®iÓm A vµ B vµ chia bÒ dµy mÆt cÇu thµnh 4 miÒn: líp BTN cã 2 miÒn a1, a2; líp bªt«ng 2 miÒn b1; b2, t−¬ng tù nh− khi trêi n¾ng. H×nh 19. §−êng cong nhiÖt ®é vμ ®−êng nhiÖt ®é H×nh 20. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã trung b×nh tuyÕn tÝnh sau m−a trong mÆt cÇu cã líp líp BTN dμy 6 cm sau m−a 12h tr−a BTN dμy 6 cm . H×nh 22. MiÒn bÞ kÐo, bÞ nÐn trong bÒ dμy mÆt cÇu cã H×nh 21. Ph©n bè nhiÖt ®é sau m−a trong mÆt cÇu cã líp BTN dμy 7,5 cm sau m−a 12h tr−a líp BTN dμy 7,5 cm
++ §Æc tÝnh kÐo nÐn sau khi m−a thÓ hiÖn trªn h×nh 16, 18, 20, 22. Cã thÓ thÊy ®Æc tÝnh kÐo nÐn kh«ng thay ®æi lu©n phiªn nhau. NghÜa lµ miÒn a1 vµ b2 lu«n bÞ kÐo, miÒn a2 vµ b1 lu«n bÞ nÐn. ¶nh h−ëng cña bÒ dμy líp BTN - BÒ dµy miÒn bÞ kÐo giíi h¹n a1 vµ miÒn bÞ nÐn a2 cña BTN: Khi bÒ dµy líp BTN t¨ng, bÒ dµy miÒn a1 vµ a2 sÏ t¨ng, nh−ng a2 t¨ng nhanh h¬n (h×nh 16, 18, 20, 22). Ng−îc l¹i khi bÒ dµy líp BTN gi¶m, miÒn a2 sÏ gi¶m nhanh sÏ tíi 0. Khi ®ã toµn bé bÒ dµy líp BTN sÏ r¬i vµo miÒn bÞ kÐo. §ã lµ tr−êng hîp bÊt lîi nhÊt nªn cã thÓ gäi bÒ dµy líp BTN ®ã lµ bÒ dµy tíi h¹n nhiÖt. ThÝ dô víi líp nhùa dµy 1,5 cm, tÝnh ®−îc miÒn bÞ kÐo dµy 2,475 cm, nghÜa lµ líp BTN dµy 1,5 cm nhá h¬n bÒ dµy tíi h¹n nhiÖt (h×nh 23). - NhiÖt ®é t¹i mÆt trªn cïng øng víi bÒ dµy líp BTN kh¸c nhau ®−îc thÓ hiÖn trªn h×nh 24. Cã thÓ thÊy lóc ®Çu mÆt ®−êng cã líp BTN dµy h¬n cã nhiÖt ®é cao h¬n chót Ýt, sau ®ã nhiÖt ®é nh− nhau. - Møc ®é bÞ kÐo m¹nh nhÊt t¹i mÆt trªn cïng cña líp BTN øng víi bÒ dµy kh¸c nhau ®−îc thÓ hiÖn trªn h×nh 25. Cã thÓ thÊy r»ng khi mÆt cÇu cã líp nhùa dµy h¬n sÏ bÞ kÐo lín h¬n, nh−ng sù chªnh lÖch lµ kh«ng ®¸ng kÓ. - Møc ®é bÞ kÐo lín nhÊt cña líp bªt«ng x¶y ra t¹i mÆt d−íi cïng vµo thêi ®iÓm p = 30 øng víi líp BTN cã bÒ H×nh 23. TÝnh to¸n miÒn kÐo nÐn øng víi líp BTN cã bÒ dμy 1,5 cm dµy kh¸c nhau thÓ hiÖn trªn h×nh 26. ThÊy r»ng líp BTN cµng máng, th× líp bªt«ng d−íi cïng bÞ kÐo cµng m¹nh. H×nh 25. Møc ®é bÞ kÐo t¹i mÆt trªn cïng líp nhùa H×nh 24. NhiÖt ®é cña líp nhùa t¹i mÆt trªn cïng lóc t¨ng khi cã bÒ dμy líp BTN t¨ng ®Çu t¨ng khi bÒ dμy líp BTN t¨ng H×nh 26. Møc ®é bÞ kÐo lín nhÊt cña líp bªt«ng t¹i H×nh 27. Møc ®é bÞ nÐn lín nhÊt trong líp nhùa vμ mÆt d−íi cïng gi¶m khi bÒ dμy líp BTN t¨ng trong bªt«ng khi cã bÒ dμy líp BTN kh¸c nhau
- Møc ®é bÞ nÐn lín nhÊt cña líp nhùa vµ bªt«ng bªn trong bÒ dµy mÆt cÇu thÓ hiÖn trªn h×nh 27. Tõ ®ã cã thÓ thÊy líp BTN bÞ nÐn lín nhÊt ë mÆt d−íi cïng t¹i vÞ trÝ tiÕp gi¸p víi bªt«ng, nh−ng bªt«ng bÞ nÐn lín nhÊt ë bªn trong vµ x¶y ra kh«ng ®ång thêi víi líp BTN. iV. KÕt luËn Tõ viÖc kh¶o s¸t mét kÕt cÊu mÆt cÇu víi líp BTN cã bÒ dµy gi¶ ®Þnh kh¸c nhau cho phÐp rót ra nh÷ng kÕt luËn sau: Khi gi¶m ®é dµy cña líp BTN trªn mÆt cÇu: 1. Vµo nh÷ng ngµy n¾ng: - L−îng nhiÖt mÆt cÇu trao ®æi víi m«i tr−êng gÇn nh− kh«ng ®æi, nhiÖt ®é cao nhÊt trong ngµy t¹i mÆt trªn líp BTN sÏ gi¶m, nhiÖt ®é trung b×nh líp BTN sÏ t¨ng, nhiÖt ®é mÆt trªn bªt«ng t¨ng. - Møc ®é bÞ kÐo t¹i mÆt trªn líp BTN kh«ng ®æi, nh−ng møc ®é bÞ kÐo t¹i mÆt d−íi líp BTN chç tiÕp gi¸p víi bªt«ng sÏ gi¶m ®¸ng kÓ. - Møc ®é bÞ nÐn cña líp BTN t¹i mÆt trªn vµ mÆt d−íi t¨ng chót Ýt kh«ng ®¸ng kÓ. 2. Khi gÆp m−a vµo buæi tr−a: - NhiÖt ®é mÆt trªn cïng cña líp BTN gi¶m h¬n chót Ýt kh«ng ®¸ng kÓ vµo lóc ®Çu, sau ®ã nhiÖt ®é nh− nhau víi c¸c bÒ dµy kh¸c nhau. - Møc ®é bÞ kÐo cña líp BTN t¹i mÆt trªn cïng gi¶m, nh−ng kh«ng ®¸ng kÓ - Møc ®é bÞ kÐo lín nhÊt cña bªt«ng ë mÆt d−íi cïng t¨ng lªn ®¸ng kÓ - Møc ®é bÞ nÐn lín nhÊt ë bªn trong líp BTN vµ bªt«ng gi¶m ®¸ng kÓ víi bÒ dµy líp BTN lín (7,5cm), nh−ng t¨ng víi líp BTN cã bÒ dµy nhá 3. Trong mäi tr−êng hîp thêi tiÕt thay ®æi, líp BTN sÏ tån t¹i ®é máng tíi h¹n nhiÖt kho¶ng gÇn 3 cm, khi ®ã toµn bé líp BTN bÞ r¬i vµo tr¹ng th¸i kÐo nguy hiÓm. Tµi liÖu tham kh¶o [1]. С.A.Φрид. Tемпературные напрЯжениЯ в бетонных и железобетонных конструкциЯх. государствнное Энергетическое издтелЬство. Москва, 1959. [2]. Frank P. Incropera. Fundametals of Heat and Mass Transfer. John Wiley & Sons. New York,1996. [3]. J. P. Holman. Heat Transfer. Mc Graw. Hill Inc. New York, 1997. [4]. Ph¹m Ngäc §¨ng. VËt lý x©y dùng. Nhµ xuÊt b¶n X©y dùng,1981♦