ph−¬ng ph¸p tÝnh to¸n
bé gi¶m dao ®éng xo¾n thñy lùc
TS. nguyÔn thµnh l−¬ng
Bé m«n §éng c¬ ®èt trong
Khoa C¬ khÝ - Tr−êng §¹i häc GTVT
Tãm t¾t: Bμi b¸o tr×nh bμy tãm t¾t ph−¬ng ph¸p tÝnh to¸n bé gi¶m dao ®éng xo¾n thñy lùc
hay bé gi¶m dao ®éng xo¾n d¹ng ma s¸t −ít. ViÖc lËp tr×nh tÝnh to¸n bé gi¶m dao ®éng xo¾n
thñy lùc phôc vô cho ch−¬ng tr×nh ch¹y tÝnh to¸n dao ®éng xo¾n hÖ trôc ®iezen - ch©n vÞt tμu
thñy phï hîp yªu cÇu quy ph¹m hÖ trôc tμu thñy cña TCVN 6259 - 3: 2003Quy ph¹m ph©n cÊp
vμ ®ãng tμu biÓn vá thÐp, phÇn 3 HÖ thèng m¸y tμu.
Summary: The article presents briefly the method of calculating an hydraulic spinning
devibrator or torsional vibration damper. The programme of devibrator calculation is used to
calculate spinning devibration in the diesel-screw-propeller axis system of a ship in accordance
with Vietnamese Standards 6259 – 3: 2003 - Rules for classification and construction of steel
ocean liners, Part 3. Machinery Installation.
CB
A
i. ®Æt vÊn ®Ò
Trong tr−êng hîp øng suÊt xo¾n do dao
®éng céng h−ëng sinh ra v−ît qu¸ ph¹m vi
cho phÐp hÖ trôc ®iªsel-ch©n vÞt sÏ bÞ gÉy.
NÕu biªn ®é dao ®éng v−ît qu¸ ph¹m vi cho
phÐp mµ tèc ®é giíi h¹n kh«ng thÓ ®−a ra
khái ph¹m vi tèc ®é lµm viÖc th× trªn hÖ trôc
®éng c¬ - ch©n vÞt buéc ph¶i dïng bé gi¶m
dao ®éng xo¾n ®Ó gi¶m thiÓu biªn ®é dao
®éng cho c¬ hÖ.
Bé gi¶m dao ®éng xo¾n cã nhiÒu lo¹i: ma
s¸t kh«, ma s¸t trong, thñy lùc, lß xo vµ con
l¾c. Bé gi¶m chÊn thñy lùc th«ng dông, trong
®ã chÊt láng silicon cã ®é nhít cao nªn dÇu
nµy cßn gäi lµ keo silic ®−îc sö dông nh− lµ
ph−¬ng tiÖn gi¶m dao ®éng. Chi tiÕt qu¸n tÝnh
(Inertia member) cã m«men qu¸n tÝnh khèi
l−îng Jd, khi ph¸t sinh céng h−ëng, khèi l−îng
nµy dao ®éng trong hép kÝn, m«men c¶n cña
chÊt láng sinh c«ng vµ tiªu hao c«ng cña qu¸
tr×nh dao ®éng céng h−ëng.
ViÖc nghiªn cøu tÝnh to¸n bé gi¶m dao
®éng xo¾n thñy lùc cã lËp tr×nh (h×nh 4.1)
nh»m phôc vô cho ch−¬ng tr×nh tÝnh to¸n dao
®éng xo¾n vµ sö dông bé gi¶m dao ®éng
xo¾n thñy lùc trªn hÖ trôc ®iªzen - ch©n vÞt tµu
thñy phï hîp yªu cÇu quy ph¹m hÖ trôc tµu
thñy cña TCVN 6259-3:2003. Sau ®©y lµ c¸c
b−íc phôc vô cho tÝnh to¸n bé gi¶m chÊn thñy
lùc.
ii. c¬ së lý thuyÕt cña bé gi¶m chÊn
thuû lùc
HÖ thèng gèc bao gåm mét khèi l−îng
r«to cã m«men qu¸n tÝnh Jm l¾p vµo ®Çu tù do
cña trôc cã ®é cøng xo¾n Cm. Bé gi¶m chÊn
bao gåm khèi l−îng chi tiÕt qu¸n tÝnh cã
m«men qu¸n tÝnh Jd n»m trong th©n vá lµ
may - ¬ ®Ó nèi bé gi¶m chÊn víi hÖ thèng gèc
cã m«men qu¸n tÝnh khèi l−îng Jh. Mèi liªn
kÕt duy nhÊt gi÷a Jd vµ Jh, cã nghÜa lµ gi÷a Jd
vµ hÖ thèng gèc lµ mét chÊt láng (silicon) cã
tÝnh gi¶m chÊn (c¶n) cã thÓ cung cÊp mét
m«men xo¾n x¸c ®Þnh Sd. M«men xo¾n kÝch
thÝch Qe t¸c ®éng lªn khèi l−îng chÝnh Jm vµ
m«men t−¬ng øng ë trªn trôc chÝnh lµ Qm
(h×nh 2.1).
Gi¶ sö momen xo¾n c¶n x¸c ®Þnh Sd tû lÖ
thuËn víi tèc ®é dao ®éng t−¬ng ®èi gi÷a Jd vµ
Jh (c¶n trong hÖ thèng gèc lµ kh«ng ®¸ng kÓ
so víi c¶n trong hÖ thèng cã l¾p bé gi¶m
chÊn). Th©n vá cña gi¶m chÊn Jh ®−îc l¾p
cøng vµo khèi l−îng chÝnh Jm sao cho hai khèi
l−îng qu¸n tÝnh ®−îc dao ®éng víi biªn ®é θm
khi mµ biªn ®é dao ®éng cña chi tiÕt qu¸n tÝnh
lµ θd.
CB
A
1. C¸c tham sè tÝnh to¸n
Ad - Tæng diÖn tÝch bÒ mÆt cña chi tiÕt
qu¸n tÝnh cña bé gi¶m chÊn, cm2 ; F - TÇn sè
c−ìng bøc, F = 60.ω/(2.π), lÇn/ phót; Ff - TÇn
sè dao ®éng tù do trong hÖ thèng cã l¾p bé
gi¶m chÊn, Ff = 60.ϖf/(2.π), lÇn/ph; Fm- TÇn sè
dao ®éng tù do cña hÖ thèng gèc,
Fm = 60.ϖm/(2.π), lÇn/ph; FP- TÇn sè cña hÖ
thèng tæ hîp ë mét ®iÓm x¸c ®Þnh, lÇn/ph;
H - L−îng nhiÖt cho phÐp, kJ/h; ht - L−îng
nhiÖt riªng, kJ/cm2.h; Jd- M«men qu¸n tÝnh
khèi l−îng cña chi tiÕt qu¸n tÝnh trong bé gi¶m
chÊn, kG.cm.sec2 ; Jh - M«men qu¸n tÝnh khèi
l−îng cña th©n vá bé gi¶m chÊn vµ may¬,
kG.cm.sec2; Jm- M«men qu¸n tÝnh khèi l−îng
cña khèi l−îng chÝnh, kG.cm.sec2 (nÕu Jh cã
gi¸ trÞ lín th× Jm ph¶i ®−îc thay b»ng (Jm + Jh)
trong nh÷ng phÇn tÝnh to¸n tiÕp theo); N - Tèc
®é vßng quay, v/ph; n - Sè thø tù cña dao
®éng, tøc lµ sè xung trong 1 vßng quay;
P - C«ng suÊt do bé gi¶m chÊn t¸n ph¸t, m·
lùc; Qb - M«men xo¾n gi¶m chÊn, kG.cm;
Qc - M«men xo¾n kÝch thÝch, kG.cm;
S
d - M«men xo¾n gi¶m chÊn riªng cña bé
gi¶m chÊn ®−îc l¾p, kG.cm cho rad/s (m«men
xo¾n x¸c ®Þnh hay tèc ®é t−¬ng ®èi);
(S
d)0 - Gi¸ trÞ tèi −u cña Sd; YP - Tû sè tÇn sè,
YP = FP/Fm; θd - Biªn ®é dao ®éng cña Jd, rad;
θr - Biªn ®é dao ®éng t−¬ng ®èi gi÷a Jd vµ Jh
hoÆc lµ gi÷a Jd vµ Jm, rad; ω - pha tèc ®é cña
lùc kÝch thÝch, rad/s; ωf - Pha tèc ®é cña dao
®éng tù do trong hÖ thèng tæ hîp cã l¾p bé
gi¶m chÊn, rad/s; ωm - Pha tèc ®é cña dao
®éng tù do trong hÖ thèng gèc, rad/s.
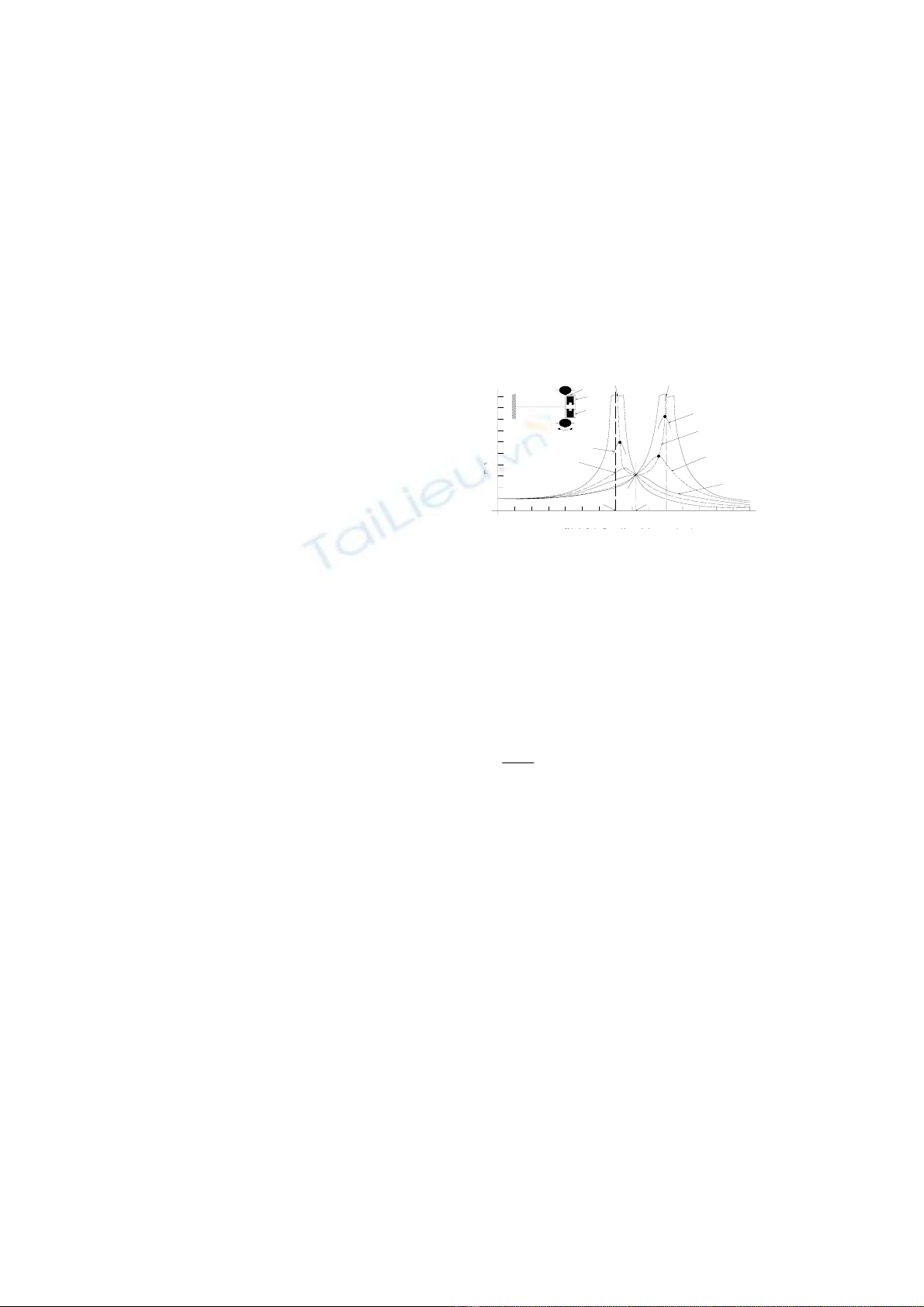
θ/θ=Qm/Qe
gi¶m chÊn tèi uu
(kd)0= 0,577
10
8
6
4
2
1,41,21,00,8
0,6
0,40,20Y=F/Fm
H×nh21:Bégim chÊnmas¸tuít
Quü tÝch
c¸c ®iÓm ®Ønh
Kh«ng l¾p
bé gi¶m chÊn
(k d= 0 )
C ã l¾p
bé gi¶m chÊn
(k d= )
Under damped
Kd = 0,25
Overdamper
(K d =1,0)
Kd = 2,0
Kd = 0,125
Jd, θd
Sd
Yf = 0,0707
Jh
Jm, θm
Yp= 0,81
Qe
Cm
Qm
P
8
m
H×nh 2.1.
2. Biªn ®é dao ®éng céng h−ëng cho
phÐp
Biªn ®é céng h−ëng cho phÐp lµ biªn ®é
ë Jm phï hîp víi øng suÊt cho phÐp lµ fS,
N/cm2 ë trªn trôc chÝnh. M«men xo¾n phï hîp
víi øng suÊt trªn trôc ®−êng kÝnh d, cm ®−îc
tÝnh theo c«ng thøc Qm = z.fs, kG.cm, ë ®©y
z lµ m«®un chèng xo¾n ®−îc tÝnh b»ng
16
d.
z
3
π
=cm3 cho trôc ®Æc ®−êng kÝnh d, cm.
Biªn ®é dao ®éng cho phÐp t¹i Jm sÏ lµ:
θm= Qm/Cm, rad hay ®é (2.2)
3. §é t¨ng ®éng häc cho phÐp ë ®iÓm
céng h−ëng
§é t¨ng ®éng häc cho phÐp lµ ®é t¨ng
®éng häc phï hîp víi øng suÊt cho phÐp
fS,N/cm2 trªn trôc chÝnh:
Mm=θm/θs (2.3)
4. M«men qu¸n tÝnh khèi l−îng cña
chi tiÕt qu¸n tÝnh trong bé gi¶m chÊn
§èi víi bé gi¶m chÊn ®−îc hiÖu chØnh
theo gi¸ trÞ tèi −u, quan hÖ gi÷a ®é t¨ng ®éng
häc cho phÐp ë ®iÓm céng h−ëng vµ tû sè
khèi l−îng ®−îc ®−a ra nh− c«ng thøc:
Mm =
()
u
u2
0
s
m+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
θ
θ (2.4a)
hay: )1M(
2
J
J
u
mm
d
−
== (2.4b)
5. M«men xo¾n gi¶m chÊn tèi −u
M«men xo¾n gi¶m chÊn tèi −u cã thÓ
®−îc tÝnh theo c«ng thøc:
[Qd/Qe] = 2/(2 + u)1/2 (2.5)
trong ®ã: (Qd)0 - gi¸ trÞ tèi −u cña m«men xo¾n
gi¶m chÊn, N.cm.
6. HiÖu chØnh m«men qu¸n tÝnh cña
trôc, cña th©n vá vµ cña may ¬ trong bé
gi¶m chÊn ®−îc l¾p
M«men qu¸n tÝnh khèi l−îng cña trôc vµ
cña th©n vá, may - ¬ trong bé gi¶m chÊn lµ
kh«ng ®¸ng kÓ. nh h−ëng cña chóng cã thÓ
®−îc tÝnh nh− d−íi ®©y.
a. M«men qu¸n tÝnh cña trôc:
CB
A
ChiÒu dµi L cña ®o¹n trôc ®Æc ®−êng
kÝnh d, cm; cã ®é cøng xo¾n Cm, N.cm/rad cã
thÓ tÝnh tõ quan hÖ L = G.
m
p
C
I, ë ®©y G
m«®un cøng G = 18498135 N/cm2 ®èi víi thÐp
vµ Ip = π.d4/32, cm4. Khèi l−îng cña trôc thÐp
dµi L cm ®−êng kÝnh d cm sÏ lµ mt kg vµ b¸n
kÝnh quay ®éc cùc sÏ lµ 8
d2
cm2. Khi ®ã
m«men qu¸n tÝnh khèi l−îng cña trôc sÏ lµ:
Js = mt.(d2/8)/91,035, N.cm.s2 (2.6a)
M«men qu¸n tÝnh khèi l−îng nµy cã thÓ
®−a vµo ®Ó tÝnh b»ng c¸ch bæ sung 1/3 cña nã
cho khèi l−îng chÝnh.
b. Th©n vá vμ may¬ cña bé gi¶m chÊn:
Theo nguyªn t¾c chung, m«men qu¸n
tÝnh khèi l−îng cña th©n vá vµ may - ¬ cña bé
gi¶m chÊn Jh b»ng 2/3 m«men qu¸n tÝnh khèi
l−îng cña chi tiÕt qu¸n tÝnh Jd, N.cm.s2. Tõ
®©y gi¸ trÞ cña th©n vá vµ may - ¬ cã thÓ tÝnh
b»ng:
Jh = 2.Jd/3 , N.cm.s2 (2.6b)
CÇn l−u ý r»ng th©n vá bé gi¶m chÊn
®−îc l¾p trùc tiÕp lªn khèi l−îng chÝnh cã gi¸
trÞ Jm sÏ lµ:
J’m = Jm + Jh + Js/3 , N.cm.s2 (2.6c)
c. Gi¸ trÞ kiÓm tra cña m«men qu¸n tÝnh
khèi l−îng cña chi tiÕt qu¸n tÝnh trong bé gi¶m
chÊn.
§Ó duy tr× øng suÊt dao ®éng lín nhÊt
trªn trôc chÝnh ë mét gi¸ trÞ giíi h¹n ®· x¸c
®Þnh lµ +fS, N/cm2 tû sè khèi l−îng sÏ kh«ng
®−îc thay ®æi t¹i U.
Tõ ®©y gi¸ trÞ kiÓm tra cña Jd sÏ lµ:
Jd = U.Jm , N.cm.s2 (2.6d)
M«men xo¾n c¶n tèi −u vµ n¨ng l−îng
sinh ra ë mét lÇn dao ®éng sÏ gièng nh−
tr−íc, cã gi¸ trÞ (Qd)0, N.cm vµ (Wd)0 , N.cm/lÇn
dao ®éng.
Tuy nhiªn, n¨ng l−îng sinh ra sÏ thay ®æi
khi t¨ng gi¸ trÞ cña Jm v× cã sù gi¶m tÇn sè tù
do trong hÖ thèng gèc vµ sù gi¶m t−¬ng øng
cña tÇn sè ë ®iÓm ®· x¸c ®Þnh, nh− sau:
F'm=9,55.(Cm/J'm)1/2 , lÇn/phót (2.6e)
vµ F'P = 0,96.F'm, lÇn/phót (2.6f)
Tõ ®©y cã c«ng suÊt tiªu hao bëi bé gi¶m
chÊn:
p' = (Wd)0.F'P/396000 , kW (2.6g)
vµ H = 3388.p' , kJ/h (2.6h)
7. KÝch th−íc cña chi tiÕt qu¸n tÝnh
trong bé gi¶m chÊn
C¸c ký hiÖu: Wi - N¨ng l−îng cña chi tiÕt
qu¸n tÝnh, N.cm/cm chiÒu réng trôc; k - b¸n
kÝnh quay, cm; R0 - ®−êng kÝnh ngoµi,cm;
Rt: ®−êng kÝnh trong, cm; ρ - khèi l−îng riªng
diÖn tÝch ngang cña vËt liÖu, ρ = 0,0198
kg/cm2 cho thÐp; Ji - m«men qu¸n tÝnh khèi
l−îng cña chi tiÕt qu¸n tÝnh, N.cm.s 2
Rt = 2
R0
()
3
R2
RR.W
2
0
2
t
2
0i =−ρπ= , N/cm (2.7a)
vµ Ji = 386
k
.w
2
i
ë ®©y k2 = (R20 + R2t)/2 = 5R20/8, cm2
Cã nghÜa lµ Ji = 37,80
R4
0,N.cm.s2 (2.7b)
Còng nh− vËy nÕu L = 3
R0 ta cã:
Wd lµ tæng khèi l−îng cña chi tiÕt qu¸n
tÝnh, Wd = 2R30/270, kg (2.7c)
vµ Jd- tæng m«men qu¸n tÝnh khèi l−îng
cña chi tiÕt qu¸n tÝnh:
Jd = 411,2
R5
0, N.cm.s2 (2.7d) CB
A
Ghi chó: §èi víi ®Üa thÐp ®Æc cã b¸n kÝnh
R0, khèi l−îng cho 1cm theo chiÒu réng trôc
sÏ lµ Wi = 0,16R0 (kg/cm), cßn m«men qu¸n
tÝnh khèi l−îng cho 1cm theo chiÒu réng trôc
sÏ lµ Ji = R04/67,7,N.cm.s2 cho 1cm theo chiÒu
réng trôc.
Còng nh− vËy tõ c«ng thøc tæng khèi
l−îng cña chi tiÕt qu¸n tÝnh
Wd=R30/135,kg (2.7e)
Tæng diÖn tÝch bÒ mÆt bªn ngoµi ®−îc
tÝnh theo c«ng thøc (h×nh 3.1)
Ad = 2π(R0 + Rt) (L + R0 – Rt), cm2 (2.7f)
Theo tû lÖ nãi trªn 2
R
Ro
t= vµ 3
R
Lo
=
Tõ ®©y ht trong c«ng thøc H = ht.Ad, kJ/h
sÏ lµ:
ht = H/Ad , kJ/dm2.h hay kJ/dm2.h (2.7g)
Gi¸ trÞ cho phÐp ht ≥ [ht] = 181,69 ÷ 227,12
kJ/dm2h ®èi víi tr−êng hîp ch¹y qua tèc ®é tíi
h¹n trong kho¶ng 800 ÷ 1000 v/ph cho bé gi¶m
chÊn nhá ch¹y trªn trôc ë tèc ®é giíi h¹n.
iii. c¸c tham sè bé gi¶m dao ®éng
xo¾n thñy lùc
1. C¸c kÝch th−íc cña th©n vá
Khe hë gi÷a c¸c bÒ mÆt ho¹t ®éng cña
chi tiÕt qu¸n tÝnh vµ th©n vá cã thÓ ®iÒu khiÓn
tÝnh tõ c«ng thøc sau:
h =
[
]
100
R.2,01 o
+ (3.1)
2. §é nhít cña chÊt láng gi¶m chÊn
C«ng thøc gi¸ trÞ tèi −u cña hÖ sè gi¶m
chÊn cho theo tû sè khèi l−îng u sÏ lµ :
(Kd)0 = [2/(1 + u)(2 + u)]1/2 (3.2a)
Do
()
md
d
d.J
S
Kϖ
=,
ë ®©y:
Jd = J'd N.cm.s2 vµ ωm = ω'm = (Cd/J'm)1/2 , rad/s
®−îc ®−a vµo ®Ó hiÖu chØnh m«men qu¸n tÝnh
khèi l−îng cña trôc, cña th©n vá vµ cña may ¬
cña bé gi¶m chÊn ®−îc l¾p.
Tõ ®©y (S'd)0 lµ gi¸ trÞ tèi −u cña m«men
xo¾n gi¶m chÊn;
(S'd)0 = J'd.ω'm(Kd)0 , N.cm.s/rad (3.2b)
Quan hÖ gi÷a (S'd)0 vµ ®é nhít cña chÊt
láng gi¶m chÊn ηt cã thÓ ®−îc x¸c ®Þnh tõ c¸c
c«ng thøc sau (ë ®©y bé gi¶m chÊn ®−îc l¾p
cã d¹ng n = 1 chi tiÕt gi¶m chÊn t−¬ng ®−¬ng
víi 1 ®Üa ®¬n).
C«ng thøc ®èi víi 2 mÆt cña ®Üa,
Sf = π.ηt.R04 (1-k4)/h , N.cm.s/rad (3.2c)
C«ng thøc ®èi víi chu vi trong vµ ngoµi
cña ®Üa:
SP = 2π.ηt.L.R30(1 + k3)/h , N.cm.s/rad
(3.2d)
Tõ ®©y, ®èi víi toµn bé ®Üa:
Sd = (Sf + SP) = π.ηt.R40[(1 - k4) +
+ 2m(1 + k3)]/h , N.cm.s/rad (3.2e)
ë ®©y: ηt - ®é nhít cña chÊt láng gi¶m chÊn ë
nhiÖt ®é vËn hµnh, N.s/cm2; R0 - b¸n kÝnh
ngoµi cña ®Üa, cm; Rt - b¸n kÝnh trong cña ®Üa,
cm; Tû sè b¸n kÝnh k = Rt/R0; L - chiÒu réng
h−íng trôc cña ®Üa, cm; Tû sè m = L/R0 ; h -
khe hë gi÷a ®Üa vµ th©n vá, cã nghÜa lµ chiÒu
dµy cña mµng chÊt láng, cm.
Tõ c«ng thøc (3.2e) tÝnh ®é nhít:
ηt=Sd.h/ π.R40[(1-k4)+2m(1+k3)], N.s/cm2
(3.2f)
3. HÖ sè gi¶m chÊn tèi −u
CB
A
Cã thÓ ®−îc x¸c ®Þnh tõ tû sè tÇn sè
yf =
m
f
F
F=[1/(1+u)]1/2 nhê c«ng thøc
(Kd)0 = Y2f.[2/(1+Y2f)]1/2 (3.3a)
§iÒu nµy phï hîp víi gi¸ trÞ ®· x¸c ®Þnh
tr−íc kia.
Trªn ®· cã tû sè:
0
c
m
0
s
m
Q
Q⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
θ
θ=(1 + Y2f)/(1 - Y2f)
Gi¸ trÞ nµy còng rÊt phï hîp víi gi¸ trÞ ®·
®−îc x¸c ®Þnh tr−íc ®ã vµ gi¸ trÞ ®−îc chØ ra
trªn h×nh 2.2.
H×nh phÝa d−íi cña h×nh 2.2 chØ ra c¸c chi
tiÕt chung cña bé gi¶m chÊn ®−îc l¾p lªn khèi
l−îng chÝnh. §é cøng cña chi tiÕt ghÐp nèi
ph¶i phï hîp víi m«men xo¾n, g©y ra bëi dao
®éng cña th©n vá vµ may ¬ (Qh) céng víi chi
tiÕt hiÖu chØnh cña m«men xo¾n ma s¸t gi÷a
chi tiÕt qu¸n tÝnh cña bé gi¶m chÊn vµ th©n vá
(QP).
Qa = (Qh + QP) , N.cm (3.3b)
ë ®©y: Qa - m«men xo¾n ®−îc truyÒn bëi bé
gi¶m chÊn cho khèi l−îng chÝnh; Qh - m«men
xo¾n do dao ®éng cña vá vµ may ¬ bé gi¶m
chÊn; QP - thµnh phÇn hiÖu chØnh cña m«men
ma s¸t gi÷a chi tiÕt qu¸n tÝnh vµ th©n vá bé
gi¶m chÊn.
NÕu nh− bé gi¶m chÊn ®−îc l¾p trùc tiÕp
víi khèi l−îng chÝnh nh− h×nh 2.2, sao cho
biªn ®é cña vá vµ may ¬ gièng nh− cña khèi
l−îng chÝnh khi ®ã:
Qh = Jh.ω2p.θm , N.cm (3.3c)
Trªn ®· cã chi tiÕt hiÖu chØnh m«men
qu¸n tÝnh khèi l−îng cña chi tiÕt qu¸n tÝnh lµ
2
Jd, tõ ®©y:
Qp = Jd.ω2p.2
m
θ, N.cm (3.3d)
iv. PhÇn lËp tr×nh tÝnh to¸n bé gi¶m
dao ®éng xo¾n thñy lùc
PhÇn lËp tr×nh ®−îc thùc hiÖn theo logic
cña c¸c b−íc tÝnh to¸n ®−a ra ë môc II vµ III
b»ng ng«n ng÷ lËp tr×nh Pascal
S¬ ®å ch¹y ch−¬ng tr×nh tr×nh bµy trªn
h×nh 4.1.
v. kÕt luËn