
TR NG ĐI H C KHOA H C T NHIÊNƯỜ Ạ Ọ Ọ Ự
KHOA CÔNG NGH THÔNG TINỆ
B MÔN C U TRÚC D LI U 2Ộ Ấ Ữ Ệ
NGUY N HOÀI PH NG Ễ ƯƠ -0212234
NGUY N H NG PHÚ Ễ Ồ -0212226
BÀI BÁO CÁO MÔN C U TRÙC D LI U 2Ấ Ữ Ệ
GVHD : Ths . Ph m Ph m Tuy t Trinhạ ạ ế
TP HCM , 2005

Cây Đ ĐenỏTháng 6 năm 2005
L i nói đu:ờ ầ
Cây đ đen là m t trong nh ng c u tr c d li u hay, cùng v i cây nh phân tìmỏ ộ ữ ấ ứ ữ ệ ớ ị
ki m là nh ng c u trúc d li u có đi m m nh trong vi c l u tr và tìm ki m dế ữ ấ ữ ệ ể ạ ệ ư ữ ế ữ
li u. Song cây đ đen có nh ng đc tính riêng mà nh đó nó đã làm n i b t nh ngệ ỏ ữ ặ ờ ổ ậ ữ
đi m m nh c a mình.ể ạ ủ
Trong ph m vi bài báo cáo này, chúng em xin trình bài v : khái quát cây đ đen,ạ ề ỏ
các thu t toán c b n, code cài đt các thu t tóan c b n và có nh ng nh n xét vậ ơ ả ặ ậ ơ ả ữ ậ ề
c u trúc cây đ đen này.ấ ỏ
Chúng em chân thành cam n cô Ph m Ph m Tuy t Trinh đã t o đi u ki n choơ ạ ạ ế ạ ề ệ
chúng em tìm hi u đ tài lý thú này. Dù h t s c c g ng song v n không tránh đcể ề ế ứ ố ắ ẫ ượ
nh ng sai xót nh t đnh chúng em mong đc s mong nh n đc nh ng đóng gópữ ấ ị ượ ư ậ ượ ữ
chân tình đ bài làm tr nên hòan ch nh h n.ể ở ỉ ơ
Nhóm th c hi n ự ệ
Sv: Nguy n Hoài Ph ng MSSV: 0212234ễ ươ
Sv:Nguy n H ng Phú MSSV: 0212226ễ ồ
Nguy n Hoài Ph ngễ ươ 2 Nguy n H ng Phúễ ồ

Cây Đ ĐenỏTháng 6 năm 2005
M c l c:ụ ụ
Nguy n Hoài Ph ngễ ươ 3 Nguy n H ng Phúễ ồ

Cây Đ ĐenỏTháng 6 năm 2005
I- Gi i thi u:ớ ệ
Cây đ đen đc ra gi i thi u b i Rudolf Bayer trong quy n “Symmetric Binary ỏ ượ ớ ệ ở ể
B-Trees: Data Structure and maintenance Algorithms”, nhà xu t b n Acta ấ ả
Informatica, Tâp1, trang 290-306. Sau đó Leonidas J.Guibas và Robert Sedgewick
đã thêm các đc tính c a cây đ đen và đt tên cho nó ( Tham kh o: Guibas, L. ặ ủ ỏ ặ ả
and Sedgewick R. “ A dichromatic Framwork for Balanced Trees”, in Proc. 19th
IEEE Symp. Foundations of Computer Science, trang 8-21, năm 1978).
Ta đã bi t cây tìm ki m nh phân thông th ng có nh ng thu n l i l n v m t ế ế ị ườ ữ ậ ợ ớ ề ặ
l u tr và truy xu t d li u trong phép toán tìm ki m thêm vào hay lo i b m t ư ữ ấ ữ ệ ế ạ ỏ ộ
ph n t . Do đó, cây tìm ki m nh phân xem ra là m t c u trúc l u tr d li u t t.ầ ử ế ị ộ ấ ư ữ ữ ệ ố
Tuy nhiên trong m t s tr ng h p cây tìm ki m nh phân có m t s h n ch .ộ ố ườ ợ ế ị ộ ố ạ ế
Nó ho t đng t t n u d li u đc chèn vào cây theo th t ng u nhiên. Tuyạ ộ ố ế ữ ệ ượ ứ ự ẫ
nhiên, n u d li u đc chèn vào theo th t đã đu c s p x p s không hi uế ữ ệ ượ ứ ự ợ ắ ế ẽ ệ
qu . Khi các tr s c n chèn đã đu c s p x p thì cây nh phân tr nên không cânả ị ố ầ ợ ắ ế ị ở
b ng. Khi cây không cân b ng, nó m t đi kh năng tìm ki m nhanh (ho c chènằ ằ ấ ả ế ặ
ho c xóa) m t ph n t đã cho.ặ ộ ầ ử
Chúng ta kh o sát m t cách gi i quy t v n đ c a cây không cân b ng: đó là câyả ộ ả ế ấ ề ủ ằ
đ đen, là cây tìm ki m nh phân có thêm m t vài đc đi m .ỏ ế ị ộ ặ ể
Có nhi u cách ti p c n khác đ b o đm cho cây cân b ng: ch ng h n cây 2-3-ề ế ậ ể ả ả ằ ẳ ạ
4. Tuy v y, trong ph n l n tr ng h p, cây đ đen là cây cân b ng hi u quậ ầ ớ ườ ợ ỏ ằ ệ ả
nh t, ít ra thì khi d li u đc l u tr trong b nh ch không ph i trong nh ngấ ữ ệ ượ ư ữ ộ ớ ứ ả ữ
t p tin.ậ
Tr c khi kh o sát cây đ đen, hãy xem l i cây không cân b ng đc t o ra nhướ ả ỏ ạ ằ ượ ạ ư
th nào. ế
Nguy n Hoài Ph ngễ ươ 4 Nguy n H ng Phúễ ồ
Cây Đ ĐenỏTháng 6 năm 2005
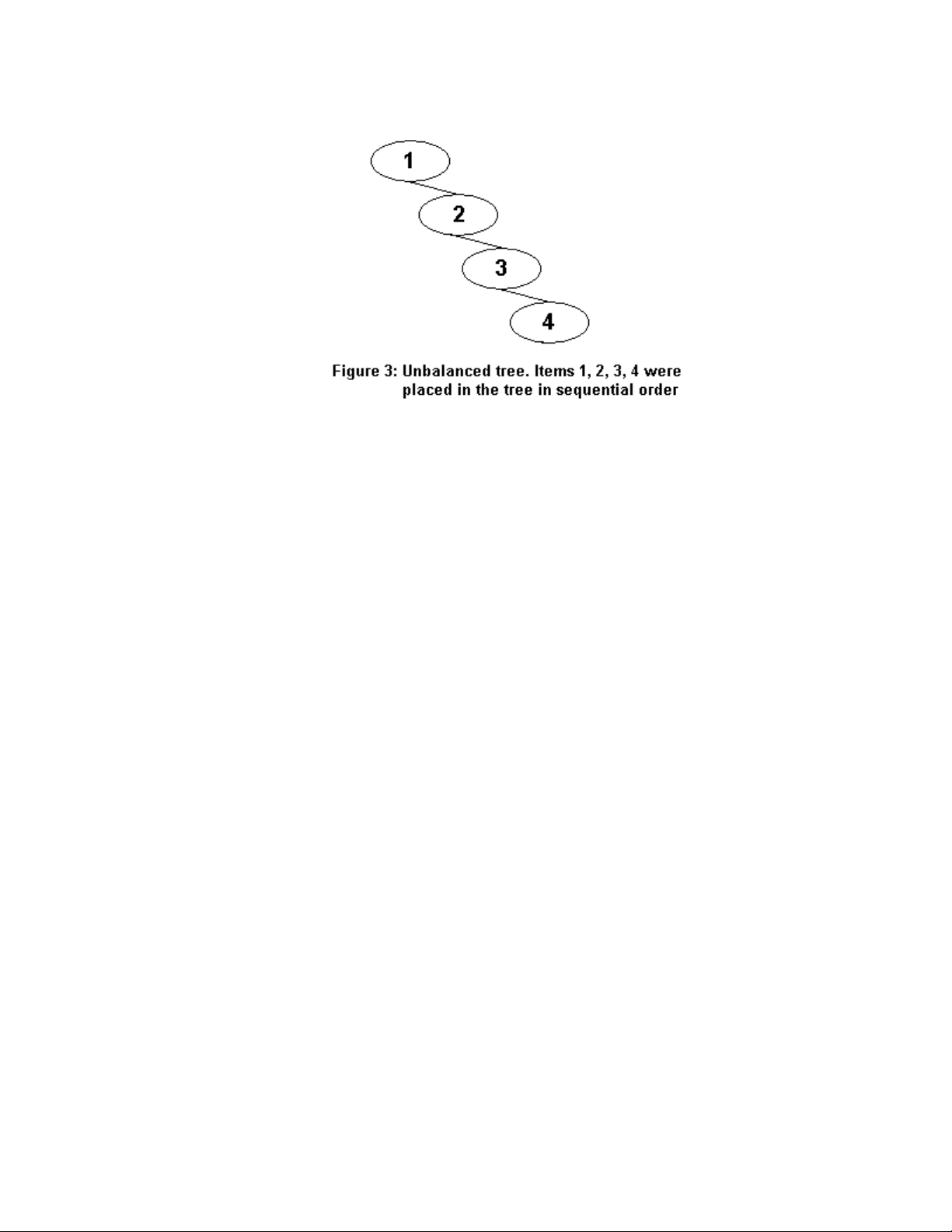
Hình 3.1. Các node đc chèn theo th t tăng d nượ ứ ự ầ
Nh ng node này t s p x p thành m t đng không phân nhánh. B i vì m i nodeữ ự ắ ế ộ ườ ở ỗ
l n h n node đã đc chèn vào tr c đó, m i node là con ph i. Khi y, cây b m tớ ơ ượ ướ ỗ ả ấ ị ấ
cân b ng hoàn toàn. N u ta chèn nh ng m c (item) theo th t gi m d n, m i nodeằ ế ữ ụ ứ ự ả ầ ỗ
s là con trái c a node cha c a chúng - cây s b m t cân b ng v phía bên kia.ẽ ủ ủ ẽ ị ấ ằ ề
* Đ ph c t p:ộ ứ ạ
Khi cây m t nhánh, s tr thành m t danh sách liên k t, d li u s là m t chi u thayộ ẽ ở ộ ế ữ ệ ẽ ộ ề
vì hai chi u. Trong tr ng h p này, th i gian truy xu t gi m v O(N), thay vìề ườ ợ ờ ấ ả ề
O(logN) đi v i cây cân b ng. ố ớ ằ
Đ b o đm th i gian truy xu t nhanh O(logN) c a cây, chúng ta c n ph i b o đmể ả ả ờ ấ ủ ầ ả ả ả
cây luôn luôn cân b ng (ít ra cũng là cây g n cân b ng). Đi u này có nghĩa là m iằ ầ ằ ề ỗ
node trên cây ph i có x p x s node con bên ph i b ng s node con bên trái.ả ấ ỉ ố ả ằ ố
M t cách ti p c n gi i quy t v n đ cân b ng l i cây: đó là cây đ đen-là cây tìmộ ế ậ ả ế ấ ề ằ ạ ỏ
ki m nh phân vì th nó có các tính ch t c a cây tìm ki m nh phân ví d : node conế ị ế ấ ủ ế ị ụ
trái nh h n node cha, node cha nh h n node con ph i, bên c nh đó cây đ đen cònỏ ơ ỏ ơ ả ạ ỏ
đc b sung m t s đc đi m.ượ ổ ộ ố ắ ể
Trong cây đ đen, vi c cân b ng đc th c thi trong khi chèn, xóa. Khi thêm m tỏ ệ ằ ượ ự ộ
ph n t thì th t c chèn s ki m tra xem tính ch t cân b ng c a cây có b vi ph mầ ử ủ ụ ẽ ể ấ ằ ủ ị ạ
hay không. N u có, s xây d ng l i c u trúc cây. B ng cách này, cây luôn luôn đcế ẽ ự ạ ấ ằ ượ
gi cân b ng.ữ ằ
II- Đnh nghĩa:ị
Cây đ đen là m t cây nh phân tìm ki m( BST) tuân th các quy t c sau: (hình 3.2)ỏ ộ ị ế ủ ắ
Nguy n Hoài Ph ngễ ươ 5 Nguy n H ng Phúễ ồ


























