TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, ĐẠI HỌC ĐÀ NẴNG - SỐ 2(37).2010
26
TỐI ƯU CÁC TRUY VẤN ĐỆ QUY HƯỚNG ĐỐI TƯỢNG DỰA TRÊN
MÔ HÌNH CHI PHÍ CƠ SỞ
OPTIMIZATION OF OBJECT-ORIENTED RECURSIVE QUERIES BASED ON
THE COST MODEL
Trương Ngọc Châu
Trường Đại học Bách khoa, Đại học Đà Nẵng
TÓM TẮT
Trong các lược đồ cơ sở dữ liệu hướng đối tượng thường xảy ra các quan hệ đệ quy
giữa các lớp, nhằm mục đích làm tăng khả năng biểu diễn ngữ nghĩa của chúng, điều này làm
phức tạp thêm vấn đề xử lý tối ưu các truy vấn nói chung và các truy vấn đệ quy nói riêng trên
các đối tượng phức. Dựa vào các kết quả trong [5], bài báo tập trung nghiên cứu, phân tích và
cải tiến các phương pháp tối ưu truy vấn đệ quy, như: tạo các cây xử lý truy vấn ứng với các
nút vị từ; biến đổi các cây xử lý truy vấn dựa trên mô hình chi phí cơ sở, sử dụng chiến lược
điều chỉnh chi phí, với tham số đầu vào là đồ thị truy vấn của truy vấn đệ quy hướng đối tượng
tổng quát.
ABSTRACT
In the schemata of object-oriented database, recursive relations among classes often
take place with the purpose of increasing the ability of performing their meaning. This causes
more problems to the optimal processing of queries in general and recursive queries based on
complicated objects in particular. Based on the results in [5], this article focuses on the study,
analysis and improvement of a number of optimal methods for recursive queries such as
creating trees of processing queries with the predicates performance at nodes; changing query-
processing trees based on a model of the basic cost by using a strategy for controlling cost with
an input querying graph of general recursive queries.
1. Giới thiệu
Các mô hình dữ liệu hướng đối tượng được mở rộng với các quan hệ đệ quy
nhằm mục đích làm tăng khả năng biểu diễn ngữ nghĩa, điều này làm phức tạp thêm vấn
đề tối ưu các truy vấn nói chung và các truy vấn đệ quy nói riêng. Các tiếp cận tối ưu
truy vấn đang tồn tại [2][3][8][10] để tối ưu hóa các truy vấn đệ quy không thể áp dụng
được.
R.S.G. Lanzelotte, P. Valduriez, M. Zait [5] đã đề xuất một cách tiếp cận tối ưu
truy vấn đệ quy hướng đối tượng dựa trên một mô hình chi phí cơ sở, sử dụng các chiến
lược điều chỉnh chi phí. Nguyên tắc chung khi tối ưu một truy vấn là biến đổi truy vấn
này về một lược đồ thực thi, có tổng chi phí là thấp nhất. Cách tiếp cận thông thường,
chủ yếu sử dụng các quy tắt viết lại truy vấn dựa trên lược đồ khái niệm [3][8][10] rất
khó để đo được chi phí thực thi. Tiếp cận của nhóm tác giả R.S.G. Lanzelotte [5] dựa
trên các thực thể vật lý, do đó chi phí của lược đồ thực thi truy vấn có thể được tính toán
trực tiếp một cách dễ dàng dựa trên mô hình chi phí đã cho.
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, ĐẠI HỌC ĐÀ NẴNG - SỐ 2(37).2010
27
Bài báo tập trung nghiên cứu và phân tích các chiến lược tối ưu dựa trên mô
hình chi phí cơ sở, sử dụng các chiến lược điều chỉnh chi phí, với tham số đầu vào là
các đồ thị truy vấn. Tiếp theo những kết quả trong [5], chúng tôi mở rộng các hành động
tối ưu một cách tổng quát hơn, dựa trên câu truy vấn đệ quy hướng đối tượng tổng quát.
2. Một số khái niệm
Ví dụ 1. Xét lược đồ cơ sở dữ liệu hướng đối tượng sau đây làm cơ sở cho các
truy vấn được trình bày trong bài báo này.
define class NGUOI:
type tuple (hoTen: String;
ngay Sinh: Date;
hocVi: String;)
end NGUOI
define class BAIGIANG:
type tuple (tenBaiGiang: String;
giaoVien: GIAOVIEN;
taiLieuTK: set(TAILIEU);)
end BAIGIANG
define class TAILIEU:
type tuple (tenTaiLieu: String;
tacGia: String;
namXB: String;)
end TAILIEU
define class GIAOVIEN inherits NGUOI
type tuple (thay: GIAOVIEN;
baiGiang: set(BAIGIANG);)
end GIAOVIEN
Ngữ nghĩa của lược đồ khái niệm trong Ví dụ 1 được giải thích như sau: một
giáo viên khi mới được nhận về giảng dạy tại một khoa ở một trường Đại học nào đó.
Giáo viên này sẽ được khoa phân công soạn một số bài giảng trước khi tham gia giảng
dạy. Các giáo viên được phân công soạn bài giảng, được khoa cử một thầy (thuộc tính
thay trong lớp GIAOVIEN) có chuyên môn liên quan hướng dẫn.
2.1. Đồ thị truy vấn [5]
Đồ thị truy vấn là một đồ thị có hướng bao gồm các thành phần sau:
- Các nút vị từ: biểu diễn các vị từ trong câu truy vấn và được ký hiệu bởi các
hình vuông, có một hoặc nhiều cung vào và một cung ra. Các cung vào và ra
của một nút vị từ được gán nhãn cây, cây này bao gồm các biến hay các đối
tượng. Nhãn cây tại cung ra của nút vị từ cho biết kiểu của nút vị từ tại đầu ra,
để ký hiệu phép chiếu tại đầu ra, chúng ta tham chiếu các biến trong các nhãn
cây của các cung vào.
- Các tên nút: là các tên lớp hay quan hệ của lược đồ khái niệm.
- Các cung có hướng nối các tên nút với các nút vị từ.
2.2. Truy vấn đệ quy
Giả sử rằng lược đồ khái niệm được mở rộng với khái niệm khung nhìn (view)
đệ quy R. Khi đó, một truy vấn đệ quy có thể được chia thành hai bước: cơ sở và đệ
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, ĐẠI HỌC ĐÀ NẴNG - SỐ 2(37).2010
28
quy, có dạng tổng quát như sau:
view R(d, i, j, v)
includes (SELECT 1, a.i, a.j, v
FROM a in T)
Truy vấn Q1 tại
bước cơ sở
Union (SELECT d+1, b.i, c.j, v
FROM b in R, c in T
WHERE <điều kiện>)
Truy vấn Q2 tại
bước đệ quy
Trong đó:
- d cho biết độ sâu của đệ quy (thuộc tính này có thể không có mặt trong truy
vấn); v có giá trị số và có thể thay đổi sau mỗi bước đệ quy, tùy thuộc vào
cách mà nó được tính toán.
- <điều kiện> chứa biểu thức kết nối b.j = c.i
- T là sưu tập chứa các đối tượng làm đầu vào cho truy vấn đệ quy
- R là sưu tập chứa các đối tượng được trả về sau mỗi bước đệ quy và có cấu trúc
tương tự như T.
Ví dụ 2. Cho truy vấn đệ quy: “Cho biết họ tên giáo viên có thầy hướng dẫn liên
quan ít nhất là 3 thế hệ, soạn các bài giảng đã tham khảo tài liệu của tác giả Nguyễn
An”.
view R(thay, giaovien, thehe)
includes (SELECT [thay: a.thay, giaovien: a, thehe: 1]
FROM a in GIAOVIEN) Bước cơ sở
Union (SELECT [thay: r.thay, giaovien: b, thehe: add1(thehe)]
FROM r in R, b in GIAOVIEN
WHERE r.giaovien = b.thay)
Bước đệ quy
SELECT kq.hoTen
FROM kq in R
WHERE kq.thehe>=3 and
kq.thay.baiGiang.taiLieuTK.tacGia = “Nguyễn An”
Trả về kết quả
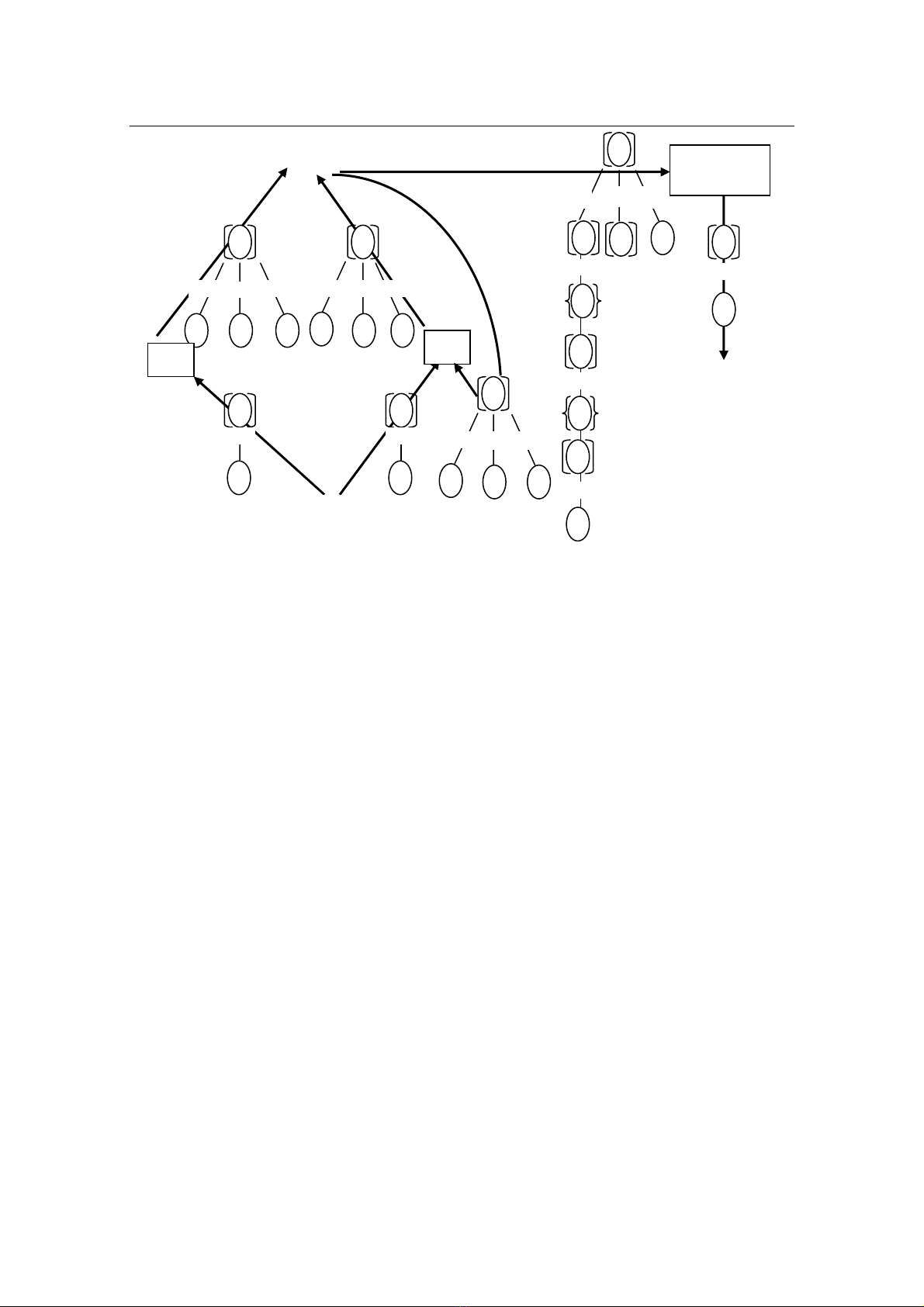
Hình 1 là đồ thị truy vấn của truy vấn trong Ví dụ 2. Các nút vị từ P1 và P2 định
nghĩa khung nhìn đệ quy R, khung nhìn này được xem như là bao đóng chuyển tiếp có
dạng R = Q1
∪
(R.Q2). Các thể hiện của R là hợp của các thể hiện ở đầu ra của các nút vị
từ P1 và P2, nút vị từ P3 áp dụng cho truy vấn trên khung nhìn đệ quy.
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, ĐẠI HỌC ĐÀ NẴNG - SỐ 2(37).2010
29
Hình 1. Đồ thị của truy vấn đệ quy
2.3. Lược đồ thực thi
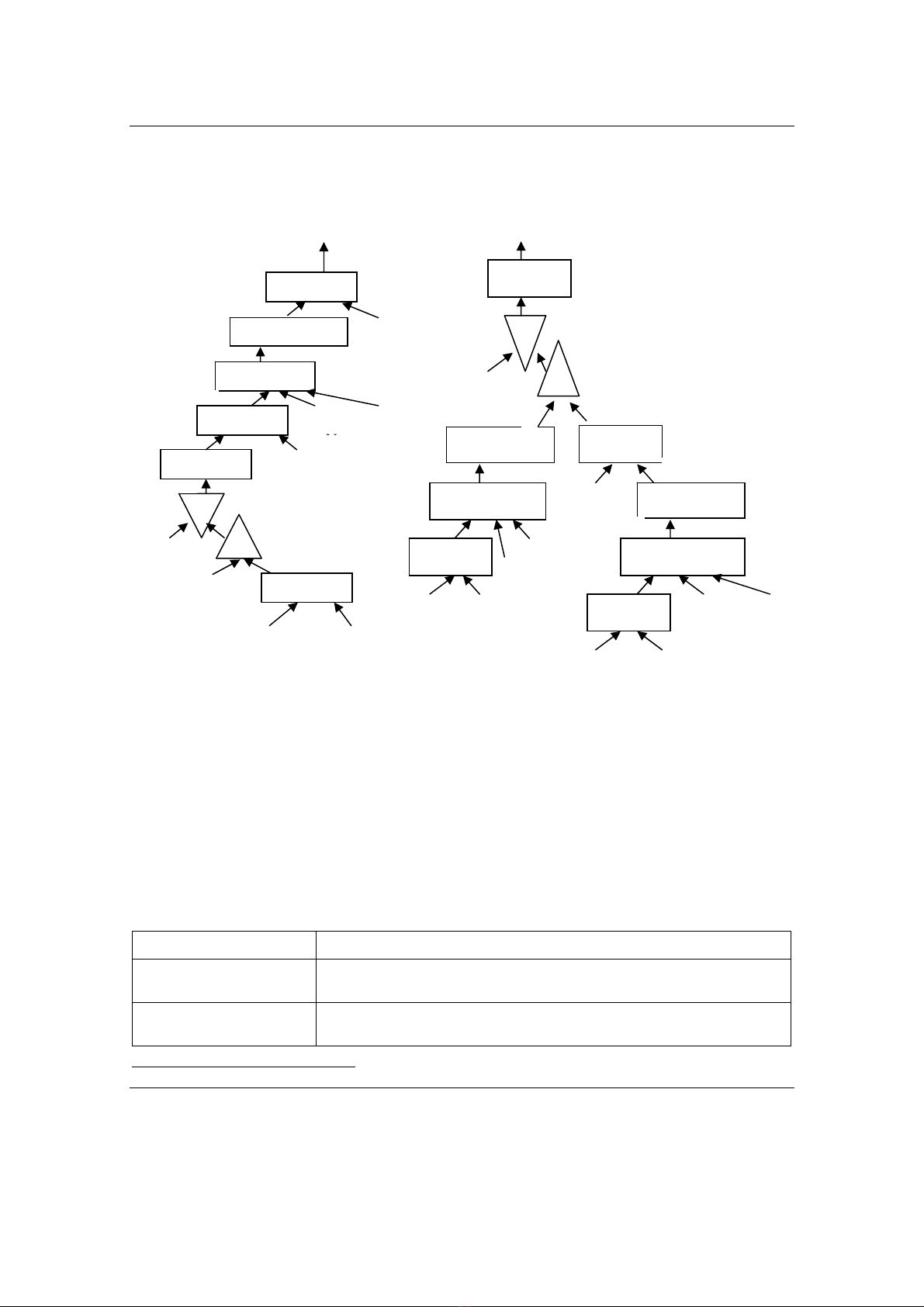
Chúng ta sử dụng cây xử lý truy vấn PT (Processing Tree) [5] để mô hình hóa
lược đồ thực thi truy vấn. Ví dụ trong Hình 2 chỉ ra hai cây xử lý truy vấn của truy vấn
ở Hình 1.
Định nghĩa. Một nút N của PT, được ký hiệu N(child0, child1,..., childk-1) sao
cho mỗi nút N hay các nút con của nó childi, 0 ≤ i ≤ k-1 hoặc là:
- Một phép chiếu Proj, một phép chọn Selpred (k = 1),
- Một kết nối ẩn IJatrrName, một kết nối hiển EJpred, một điểm bất động (Fix point)
Fix, một phép hợp Union (k = 2),
- Một kết nối ẩn thực hiện bởi một chỉ mục đường dẫn PIJpathIndex (k ≥ 2),
- Một thực thể nguyên tử của lược đồ vật lý hoặc một tập tin tạm (k = 0).
2.4. Mô hình chi phí [4, 5, 6]
Ký hiệu Ci là tên của quan hệ hay lớp, N là nút của PT, Ai là thuộc tính của Ci, P
là vị từ. Ta có chi phí cho các phép toán cơ bản như sau:
+ access_cost(Ci): chi phí truy cập các thể hiện của Ci.
+ access_cost(Ci, P): chi phí truy cập các thể hiện của Ci thỏa mãn vị từ P.
+ access_cost(Ci, Ci+1): chi phí truy cập các thể hiện của Ci+1 được tham chiếu bởi
một thể hiện của Ci thông qua thuộc tính Ai.
+ eval_cost(Ci, P): chi phí ước lượng vị từ P trên tất cả các đối tượng của Ci được
lưu trữ trong một trang của Ci.
P2
P1
x
y
thay
x 1
giaoviethehe
TRUE
thay
y
GIAOVIEN
R
x
thay
y
y = d
thay
g
giaovie theh
m
thay
d g
giaovie add1
baiGiang
d
taiLieuTK
tacGia
i
i = “Nguyễn An”
and g >= 3 P3
d
hoTen
m
KETQUA
m
thay
x
giaovienthehe
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, ĐẠI HỌC ĐÀ NẴNG - SỐ 2(37).2010
30
- Các tham số dựa trên mô tả của lược đồ vật lý: |Ci| số các trang mà Ci được lưu
trữ; ||Ci|| số các thể hiện của Ci; nblevels(I) số cấp của chỉ mục I; nbleaves(I) số các nút
lá của chỉ mục I.
Hình 2. Các cây xử lý cho truy vấn của Hình 1.
- Các hàm:
+ nbpages(Ci, P): trả về số các trang đã truy cập, nghĩa là |Ci| đã được rút gọn
bởi vị từ P.
+ nbtuples(Ci, P): trả về số đối tượng đã truy cập, nghĩa là ||Ci|| đã được rút gọn
bởi vị từ P.
Bảng 1. Các công thức tính chi phí cho các nút trong cây xử lý truy vấn
Nút của PT Công thức chi phí
Selselpred(C) access_cost(C, selpred) + nbpages(C, selpred)*eval_cost(C,
selpred)
EJpred(Ci, Cj) access_cost(Ci, pred) + nbtuples(Ci, pred)*(access_cost(Cj,
pred) + nbpages(Cj, pred) * eval_cost(Cj, pred)) 1
1 Công thức này là hợp lệ nếu phép toán EJ được thực hiện bằng cách sử dụng thuật toán kết nối lặp lồng
hay chỉ mục kết nối.
R
GIAOVIEN R
EJthay =
∪
F
ix
Selthehe ≥ 3
IJthay
PIJbaiGiang.taiLieuT
KETQUA
SeltacGia = ‘Nguyễn An’
IJgiaovien
GIAOVIEN
GIAOVIEN
GIAOVIEN
GIAOVIE
N
R
T1
T
2
T3
T4
T6
T5
(i)
GIAOVIEN
TAILIEU
IJthay
GIAOVIEN IJthay
R’ GIAOVIEN
PIJbaiGiang.taiLieuTK
BAIGIANG TAILIEU
SeltacGia = ‘Nguyễn
GIAOVIEN
EJthay =
PIJbaiGiang.taiLieuTK
BAIGIAN
G
SeltacGia = ‘Nguyễn
∪
Fi
Selthehe ≥ 3
KETQUA
R’
T7
T8
T9
T10
T11
T12
T13
T14
T15
(ii)