Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc
………………………………..........150
q
00
π
0
+ q
10
π
1
+ q
20
π
2
+... = 0,
q
01
π
0
+ q
11
π
1
+ q
21
π
2
+... = 0,
q
02
π
0
+ q
12
π
1
+ q
22
π
2
+... = 0,
....
Do tính ch
t
ñ$
c bi
t, nh
ư
ñ
ã phân tích
*
trên, c
a ma tr
n c
ư
ng
ñ
Q c
a quá trình
sinh
−
t
#
, h
trên
ñư
c vi
t m
t cách t
ư
ng minh h
ơ
n nh
ư
sau:
−λ
0
π
0
+
µ
1
π
1
+... = 0,
λ
0
π
0
−
(
λ
1
+
µ
1
)
π
1
+
µ
2
π
2
+... = 0,
λ
1
π
1
−
(
λ
2
+
µ
2
)
π
2
+
µ
3
π
3
+... = 0,
...
T
"
ñ
ây
ñ.
dàng tìm
ñư
c
π
n+1
= (
λ
n
/
µ
n+1
)
π
n
,
∀
n = 1, 2, 3,...
ñ
ñ
i t
i công th
c tính
π
i
,
∀
i.
π
1
= (
λ
0
/
µ
1
)
π
0
,
π
2
= (
λ
1
/
µ
2
)
π
1
= (
λ
1
λ
0
/
µ
2
µ
1
)
π
0
,
π
3
= (
λ
2
/
µ
3
)
π
2
= (
λ
2
λ
1
/
µ
3
µ
2
)
π
1
= (
λ
2
λ
1
λ
0
/
µ
3
µ
2
µ
1
)
π
0
,
...
π
n+1
= (
λ
n
/
µ
n+1
)
π
n
=... = (
λ
n
λ
n−1...
λ
0
/
µ
n+1
µ
n...
µ
1
)
π
0
,
...
V
i
ñ
i
u ki
n
i
i 0
1,
∞
=
π =
∑
cu
i cùng ta có:
π
0
= 1/(1 + ∑
∞
=0k
(λ
k
λ
k−1...
λ
0
/µ
k+1
µ
k...
µ
1
)).
ð$
c bi
t khi µ
n
= 0, ∀n thì quá trình sinh−t
#
tr
*
thành quá trình sinh thu
n khi
t
(
pure birth process
). Quá trình sinh thu
n khi
t v
i λ
n
= λ
là quá trình Poát−xông v
i
tham s
λ
.
Ví d 2: Gi s# dòng khách hàng ñn mua vé * mt văn phòng bán vé vi M qu y
phc v là dòng Poát−xông vi tham s λ = 6 khách hàng/1 phút (ñiu này cũng có
nghĩa là khách hàng ñn phòng bán vé vi các thi ñim ñn tuân theo lut phân phi
mũ vi tham s λ = 6).
Ngoài ra, còn bit nguyên tc phc v là FCFS (First come first served) và thi gian
phc v ti m&i qu y có lut phân phi mũ vi kì vng 1/3 (phút).
C n tr li hai câu hi sau ñây:
− S qu y hàng ti thiu là bao nhiêu ñ hàng ch không tr* nên dài vô hn?
− Gi s# N
t
là s khách hàng ñang ch hay ñang ñưc phc v ti thi ñim t. Chn
M = 4 và mt khách hàng s, ch ñ ñưc phc v nu N
t
≤ 4, ch vi xác sut 0,5 nu
N
t
= 5 và s, b ñi nu N
t
= 6. Hãy xác ñnh phân phi d"ng ca quá trình này?
Trưc ht, trong ví d này chúng ta có mt quá trình sinh−t# vi không gian trng
thái S = {S
0
, S
1
, S
2
,..., S
n
,...}, trong ñó S
n
là trng thái trong văn phòng có n khách hàng.
Các cưng ñ chuyn là λ
k
= 6 vi k = 0, 1, 2,... còn µ
k
= 3k vi k ≤ M và µ
k
= 3M vi
k > M. ðiu này là do bin cc tiu ca các bin ngu nhiên vi phân phi mũ ñc
lp cũng có phân phi mũ vi tham s bng tng các tham s ca các phân phi
mũ tương ng. Tht vy, gi s# X = Min {X
1
, X
2
} vi X
1
và X
2
tuân theo phân
phi mũ ñc lp vi các tham s µ
1
và µ
2
, th thì P(X ≥ t) = P(X
1
≥ t) P(X
2
≥ t) =
1 2 1 2
t t ( )t
e e e
−µ −µ − µ +µ
=
. Do ñó X có phân phi mũ vi tham s µ = µ
1
+ µ
2
.
Do λ
k
/µ
k+1
= 6/3M < 1 (khi k ≥ M) nên vi M ≥ 3 thì:
∑
∞
=0k
k k 1 0 k 1 k 1
( ... / ... )
− +
λ λ λ µ µ µ
< ∞.
B*i vy hàng ñi s, không dài vô hn (nu trái li, khi chu&i phân kì thì
0 1 2
... 0,
π = π = π = =
nên s khách trong hàng ñi s, d n ti mt s h(u hn khi t → ∞
vi xác sut bng 0).
Trong câu hi th hai, ta có λ
0
= λ
1
= λ
2
= λ
3
= λ
4
= 6, λ
5
= 3. Theo công thc tính
5
0
k 0
1/(1
=
π = +
∑
k k 1 0 k 1 k 1
( ... / ... ))
− +
λ λ λ µ µ µ
ta có ngay π
0
= 12/89. T
"
ñ
ó tính ra
π
1
= 24/89,
π
2
= 24/89, π
3
= 16/89, π
4
= 8/89, π
5
= 4/89 và π
6
= 1/89.
3. MÔ PH$NG XÍCH MARKOV
3.1. Mô ph%ng xích Markov th(i gian r(i rc
Phương pháp 1
Xích Markov ri rc và thu n nht còn có th ñưc kí hiu là X
0
, X
1
, X
2
,... Gi s#
không gian trng thái là S gm h(u hn trng thái: S = {0, 1, 2,..., N} và ma trn xác
sut chuyn trng thái ñã ñưc bit là P = [p
ij
]
N
×
N
. Chúng ta s, mô phng xích Markov
ri rc và thu n nht thông qua ví d ñã trình bày * các mc 1.2 và 2.1 ca chương này.
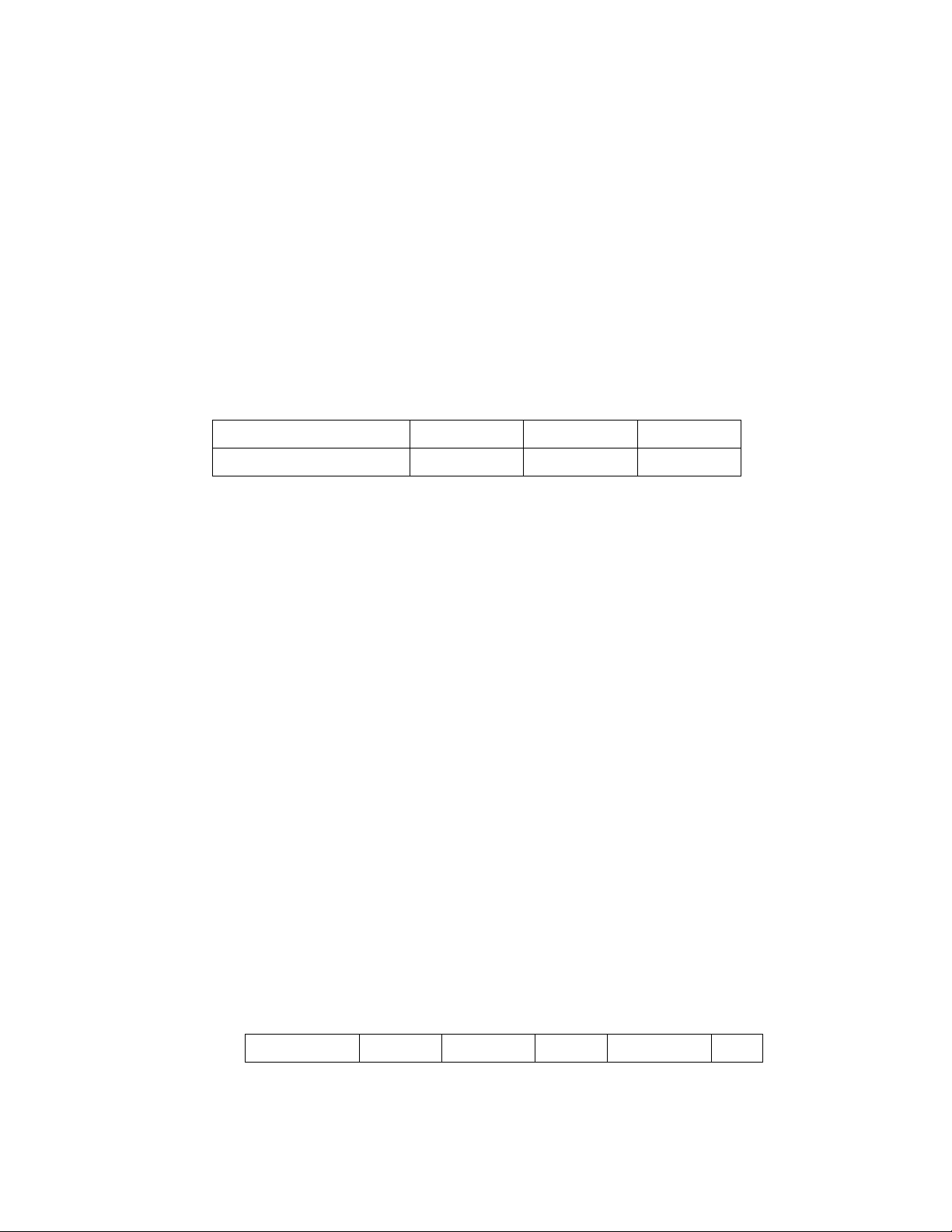
Ta có phân phi ban ñ u là:
X
0
1 2 3
Π
(0)
π
1(0)
= 0,2 π
2(0)
= 0,5 π
3(0)
= 0,3
Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc
………………………………..........152
ð mô phng X
0
ta áp dng phương pháp mô phng phân phi ri rc ñã hc *
chương III. Trên máy tính, ta phát sinh ra mt s ngu nhiên r = RANDOM[0,1) theo
lut phân phi ñu U[0,1) trong [0,1). Nu r ≤ 0,2 ta ly X
0
= 1; nu 0,2 < r ≤ 0,7 thì ta
ly X
0
= 2 ; còn nu r > 0,7 thì ñ$t X
0
= 3. Căn c kt qu mô phng X
0
, ta mô phng
X
1
da trên ma trn xác sut chuyn trng thái:
P =
083,0
07,0
8,0
067,0
9,0
1,0
85,0
03,0
1,0
.
Gi
s
#
ñ
ã bi
t X
0
= 2, lúc
ñ
ó ta c
n mô ph
ng bi
n ng
u nhiên X
1
c
ă
n c
phân ph
i
sau:
X
1
1 2 3
Xác sut tương ng
p
21
= 0,07 p
22
= 0,9 p
23
= 0,03
ð
i
u này có th
ñư
c th
c hi
n t
ươ
ng t
nh
ư
khi mô ph
ng X
0
. C
n chú ý r
ng,
trong hàng th
hai c
a b
ng trên ta có phân ph
i xác su
t có
ñ
i
u ki
n c
a X
1
v
i
ñ
i
u
ki
n X
0
= 2. Các b
ư
c ti
p theo mô ph
ng X
2
, X
3
,...
ñư
c ti
n hành t
ươ
ng t
(cho t
i
X
500
ch
-
ng h
n).
L
$
p l
i quy trình này b
t
ñ
u t
"
X
0
cho m
t s
b
ư
c l
$
p L
ñ
l
n (ch
-
ng h
n 1000
l
n), ta s
,
có m
t b
1000 s
li
u cho X
500
. T
"
ñ
ó, có th
tìm
ñư
c b
ng phân ph
i t
n
su
t (còn g
i là xác su
t th
c nghi
m) c
a X
500
qua thí nghi
m mô ph
ng trên
ñ
ây
ñ
i
v
i X
500
. Nh
ư
v
y, ta tìm
ñư
c véc t
ơ
phân ph
i (xác su
t th
c nghi
m)
Π
(500)
. Cu
i
cùng, chúng ta có k
t qu
tìm g
n
ñ
úng phân ph
i d
"
ng là:
Π
≈
Π
(500)
.
Chú ý:
−
Trong ví d
trên
ñ
ây, ta th
y có th
dùng mô ph
ng
ñ
tìm phân ph
i d
"
ng. Tuy
nhiên, m
c
ñ
ích ch
y
u c
a ph
ươ
ng pháp 1 là nh
m mô ph
ng các xích Markov r
i r
c
thu
n nh
t, là các quá trình có th
x
y ra trong các h
th
ng ph
c t
p.
−
Khi không gian tr
ng thái S g
m m
t s
l
n các tr
ng thái thì ph
ươ
ng pháp mô
ph
ng trên yêu c
u th
i gian ch
y máy tính khá l
n.
ð
kh
c ph
c
ñ
i
u này, chúng ta
xem xét ph
ươ
ng pháp 2 sau
ñ
ây.
Phương pháp 2
Xét m
t h
th
ng k
ĩ
thu
t
ñư
c bi
u di
.
n b
*
i xích Markov r
i r
c thu
n nh
t {X
t
}, t
= 0, 1, 2,... v
i không gian tr
ng thái S có N tr
ng thái (N khá l
n) và ma tr
n chuy
n
tr
ng thái P = [p
ij
]
N
×
N
. Xét th
i
ñ
i
m n, t
i th
i
ñ
i
m này gi
s
#
ñ
ã mô ph
ng
ñư
c X
n
=
s. Ta s
,
mô ph
ng th
i gian T
n
là th
i gian t
i l
n nh
y ti
p theo s
m nh
t mà X
t+Tn
≠
s.
Do xích Markov là r
i r
c nên T
n
ch
có th
nh
n các giá tr
1, 2,...
ð$
t p = p
ss
, d
.
th
y
T
n
có phân ph
i hình h
c nh
ư
sau:
T
n
1 2 ... k ...
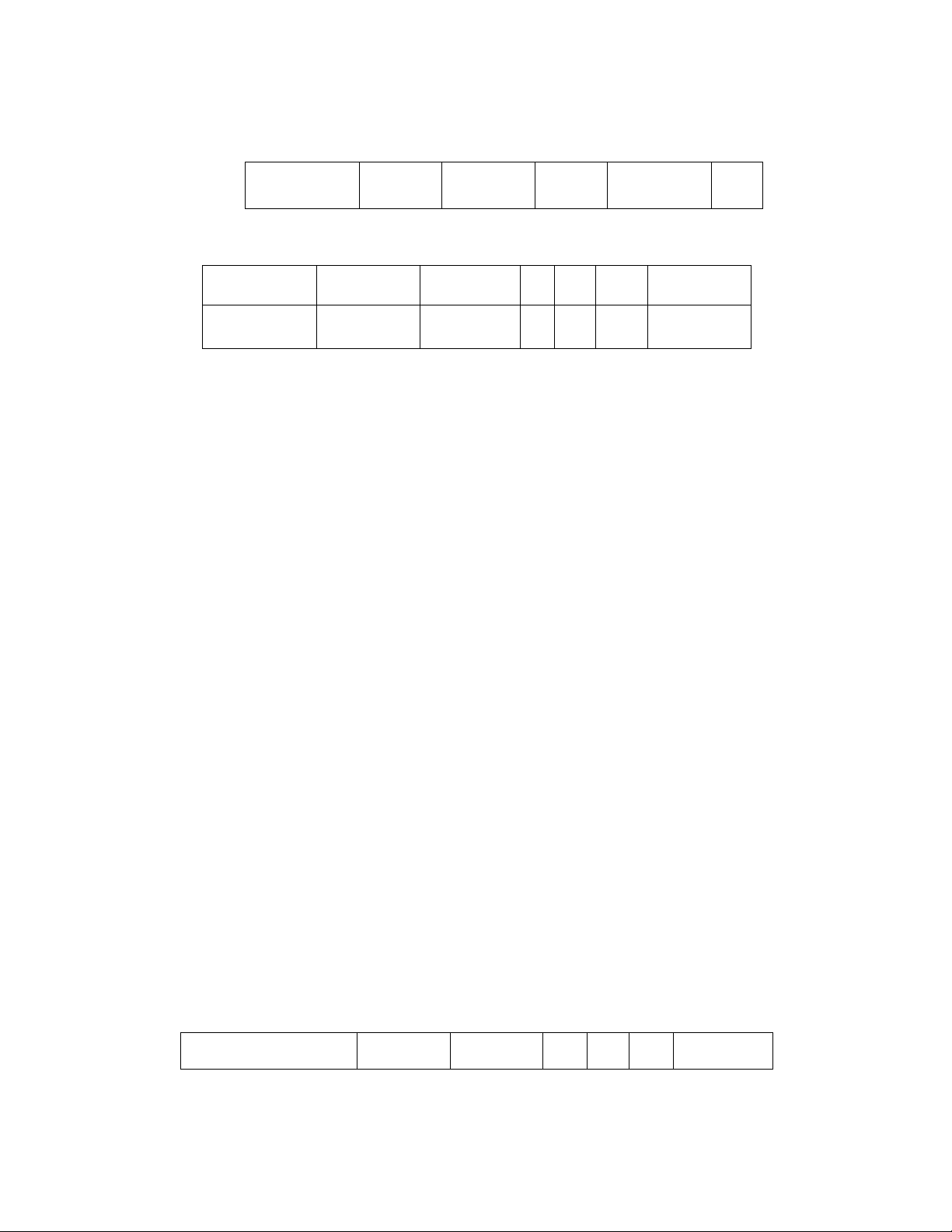
Xác sut
tương ng 1−p (1−p)p ... (1−p)p
k−1
...
Mô ph
ng phân ph
i này ta tìm
ñư
c giá tr
T
n
.
Còn X
n+Tn
có phân ph
i xác su
t
nh
ư
sau:
X
n+Tn
1 2 ... s ... N
Xác sut
tương ng p
s1
/(1−p
ss
) p
s2
/(1−p
ss
) ... 0 ... p
sN
/(1−p
ss
)
Cách mô ph
ng này s
,
ti
t ki
m h
ơ
n th
i gian ch
y máy tính (khi N khá l
n),
nh
ư
ng vi
c l
p trình s
,
ph
c t
p h
ơ
n ít nhi
u.
Xét ví d
nh
ư
ñ
ã trình bày trên, n
u dùng ph
ươ
ng pháp 2, m
t cách hoàn toàn t
ươ
ng
t
, chúng ta c
ũ
ng tìm
ñư
c phân ph
i d
"
ng
Π
(*)
≈
Π
(500)
.
3.2. Mô ph%ng xích Markov th(i gian liên tc
Xét xích Markov thi gian liên tc {X(t)}
t∈
∈∈
∈[0, ∞
∞∞
∞)
. Gi s# rng xích ñi vào trng thái i
ti thi ñim nào ñó, ch-ng hn thi ñim 0 và không ri khi trng thái này cho ñn
thi ñim s. Lúc ñó, do tính “không nh” ca quá trình Markov, xác sut ñ xích vn
tip tc * nguyên trng thái ñó cho ti thi ñim (t + s) s, là:
P{(T
i
> s + t )/(Ti > s)} = P{T
i
> t}
trong ñó T
i
là thi gian quá trình d"ng li * trng thái i. D. thy, nu T
i
có phân
phi mũ vi hàm phân phi F(T
i
< τ) = 1 - e
−λτ
thì ñ-ng thc trên ñưc tho mãn. ðiu
ngưc li cũng có th chng minh ñưc. Vy T
i
có phân phi mũ.
T" nhn xét trên, ta có th ñưa ra mt ñnh nghĩa khác cho xích Markov thi gian
liên tc. Xích Markov thi gian liên tc là mt quá trình ngu nhiên có các tính cht sau
m&i khi nó ñi vào trng thái i:
− Lưng thi gian T
i
xích d"ng li ti trng thái i trưc khi nó chuyn sang trng
thái khác là mt bin ngu nhiên vi phân phi mũ có tham s v
i
(hay có kì vng 1/v
i
).
− Mt khi quá trình ri khi trng thái i, nó s, ñi vào trng thái j nào ñó (ñc lp vi
T
i
) vi các xác sut p
ij
tho mãn
= = ∀
∑
.
Vy ñ mô phng xích Markov thi gian liên tc, chúng ta c n mô phng dãy τ
0
, τ
1
,
τ
2
,... (các lưng thi gian τ
r
xích d"ng li ti trng thái J
r
trưc khi nó chuyn sang trng
thái khác) và dãy J
0
, J
1
, J
2
,... (các trng thái mà xích chuyn ñn). ð phát sinh τ
r,
như
trên ñã nói, ta c n bit tham s v
Jr
ca phân phi mũ tương ng. Còn ñ phát sinh trng
thái xích Markov chuyn ñn J
r
∀r, chúng ta có bng phân phi xác sut sau:
Trng thái ñn 1 2 ... i ... N
Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc
………………………………..........154
Xác sut tương ng p
i1
p
i2
... 0 ... p
iN
Trong bng trên, i =J
r
-
1
là trng thái ca xích ti bưc r − 1 (vi các xác sut p
ij
tho
mãn
= = ∀
∑
).
ð thc hin mô phng xích Markov thi gian liên tc, có th s# dng s liu ca ví
d ñã xét trong mc 2.4 hay 2.5.
BÀI TP CHƯƠNG V
1. Ch s tiêu th ñin là mt lưng ngu nhiên có phân phi ti thi ñim ban ñ u
như sau:
X
0
Dưi 50 s 50 ti 100 100 ti 150 Trên 150
T l % 5% 40% 40% 15%
Bit ma trn xác sut chuyn trng thái là:
P =
05,0
02,0
05,0
85,0
05,0
03,0
85,0
10,0
10,0
90,0
08,0
05,0
80,0
05,0
02,0
0
−
Hãy gi
i thích ý ngh
ĩ
a c
a ma tr
n P.
−
Tìm phân ph
i d
"
ng c
a xích Markov th
i gian r
i r
c trên
ñ
ây và cho bi
t ý
ngh
ĩ
a c
a k
t qu
thu
ñư
c.
2.
M
t ch
trang tr
i tr
ng hoa hàng n
ă
m th
c hi
n phân tích thành ph
n
ñ
t c
a
trang tr
i. K
t qu
phân tích
ñư
a ra
ñ
t thu
c vào m
t trong ba tr
ng thái: t
t, bình
th
ư
ng và x
u. Các kh
o sát th
ng kê cho bi
t các ma tr
n xác su
t chuy
n tr
ng thái
(sau m
t n
ă
m) trong các tr
ư
ng h
p không bón phân và có bón phân (h
(
u c
ơ
) nh
ư
sau:
1
0,2 0,5 0,3
P 0 0,5 0,5
0 0 1
=
và
2
0,3 0,6 0,1
P 0,1 0,6 0,3
0,05 0,4 0,55
=
.
Các ma tr
n l
i nhu
n/n
ă
m (
ñơ
n v
tính là 10 ngàn USD) t
ươ
ng
ng v
i các ma tr
n
xác su
t chuy
n tr
ng thái trên là:
1
7 6 3
R 0 5 1
0 0 1
=
−
và
2
6 5 1
R 7 4 0
6 3 2
−
=
−
.
![Tài liệu ôn tập thiết kế mạng máy tính [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250420/hoangquadz/135x160/5651745155816.jpg)
