Các mô hình mạng 9: Tổng quan và ứng dụng

Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc

………………………………..........180

Chú ý: Có th chng minh ñưc rng nu hàm tha dng u(.) là hàm li (li ng$t)

thì π ≤ 0 (< 0) vi mi cuc x s. Còn nu hàm tha dng u(.) là hàm lõm (lõm ng$t)

thì π ≥ 0 (> 0) vi mi cuc x s.

Quay li ví d ñang xét, do hàm u(.) vi ñ th u

ñã xây dng là li ng$t nên ta luôn

có π = E(x/p) – u

−1

(E(u/p)) < 0. ðiu này cũng có nghĩa là u(E(x/p)) < E(u/p), tc là ñ

tha dng ca kì vng li nhun là nh hơn kì vng tha dng do cuc x s mang li.

Trong trưng hp hàm tha dng có ñ th u

(trên hình V.4) thì π > 0 và do ñó

u(E(x/p)) > E(u/p), tc là ñ tha dng ca kì vng li nhun là ln hơn kì vng tha

dng do cuc x s mang li. T" các phân tích trên, ta thy nu ngưi ra quyt ñnh có

hàm tha dng u(.) li thì ngưi ñó có tính “hưng mo him” (Risk Prone), còn nu

trái li, u(.) lõm thì có tính “tránh mo him” (Risk Averse). Vi u(.) tuyn tính, ngưi

ra quyt ñnh có tính hp lí (Risk Neutral).

ðiu này ñưc th hin khá trc quan trên hình V.4 nu ta quy li thang bc gii

thư*ng: thay vì các cuc x s “bo him” ñã nói ti trong ví d, chúng ta xét các cuc

x s tht s vi gii thư*ng (ñưc quy li gc ta ñ) thuc vào khong 0 USD ti

150000 USD. Vi ñ th u

ta thy, * các gii thư*ng khá cao ngưi ra quyt ñnh có

tính “hưng mo him” vn ch có ñ tha dng (mc ñ tha mãn) thp, ch-ng hn

gii thư*ng 149500 USD ch mang li ñ tha dng là 0,7 và ñ tha mãn tăng rt

nhanh khi mc gii thư*ng tăng sát 150000 USD. ð th u

cũng có th ñưc phân tích

tương t ñ thy tính “tránh mo him” ca ngưi ra quyt ñnh.

Ví d 2: Mt nhà ñ u tư có 10000 USD có th ñ u tư vào th trưng chng khoán.

Anh ta có th la chn hai công ti X và Y ñ ñ u tư (gi s# rng hai công ti X và Y là

hoàn toàn ñc lp vi nhau).

Theo tính toán sơ b và d ñoán ca chuyên gia thì nhà ñ u tư có th nhn ñưc gp

ñôi s tin ñ u tư vi xác sut 0,6 và có th mt ñi mt n#a s tin ñ u tư vi xác sut

0,4 khi ñ u tư vào mt trong hai công ti trên. Anh ta xem xét các la chn sau:

- ð u tư toàn b s tin vào mt trong hai công ti (phương án A).

- ð u tư 5000 USD vào công ti X (phương án B).

- ð u tư 5000 USD vào công ti X và 5000 USD vào công ti Y (phương án C).

- Không ñ u tư vào hai công ti trên (phương án D).

Ngoài ra, gi s# ñã bit hàm tho dng ca ngưi ñ u tư ti mt s mc li nhun:

u(−5000) = 0; u(−2500) = 0,2; u(0) = 0,4; u(2500) = 0,7; u(5000) = 0,9; u(10000) = 1.

Hãy xác ñnh phương án ñ u tư da trên tiêu chu%n kì vng tho dng ti ña.

Tính kì vng tho dng cho phương án A: E(u/p

) = 0,6×u(10000) + 0,4×u(−5000)

= 0,6. Tương t, E(u/p

) = 0,6×u(5000) + 0,4×u(−2500) = 0,6×0,9 + 0,4×0,2 = 0,62

Nhm tính kì vng tho dng cho phương án C, chúng ta s# dng hàm sinh

(0,6a

+ 0,4 b

)(0,6a

+ 0,4 b

) = 0,36 a

+ 0,24a

+ 0,24b

+ 0,16b

ñ xác ñnh ñưc các xác sut: xác sut ñ u tư vào c hai công ti cùng lãi là 0,36; xác

sut ñ u tư vào công ti X lãi và công ti Y l& là 0,24; xác sut ñ u tư vào công ti X l& và

công ti Y lãi là 0,24; xác sut ñ u tư vào c hai công ti cùng l& là 0,16.

Vy E(u/p

) = 0,36×u(10000) + 0,24×u(2500) + 0,24×u(2500) + 0,16×u(−5000) =

0,36×1 + 0,24×0,7 + 0,24×0,7 + 0,16×0 = 0,696. D. thy E(u/p

) = 0,4. Do ñó, da trên

tiêu chu%n kì vng tha dng ti ña, ta chn phương án C ñ ñ u tư.

Chú ý: Ra quyt ñnh da trên tiêu chu%n kì vng tho dng ti ña là mt phương

pháp ra quyt ñnh trong môi trưng ri ro. Cái khó nht trong phương pháp này là thit

lp ñưc hàm tho dng.

Ví d 3: Mt nhà ñ u tư nghiên cu v c phiu ca mt công ti và ñánh giá rng

các c phiu s, tăng giá trong thi gian ti. Hin ti mt c phiu ñưc bán ra vi giá

50 USD. Thông qua ngưi môi gii, nhà ñ u tư ñưc gii thiu ñ mua mt hp ñng

như sau: mua 4 USD/quyn mua mt c phiu vi giá 48 USD/c phiu trong vòng hai

tháng n(a. Nhà ñ u tư cũng ñưc ñ ngh mt hp ñng khác: mua 8 USD/quyn mua

mt c phiu vi giá 48 USD/c phiu trong vòng bn tháng n(a. Nhà ñ u tư thu thp

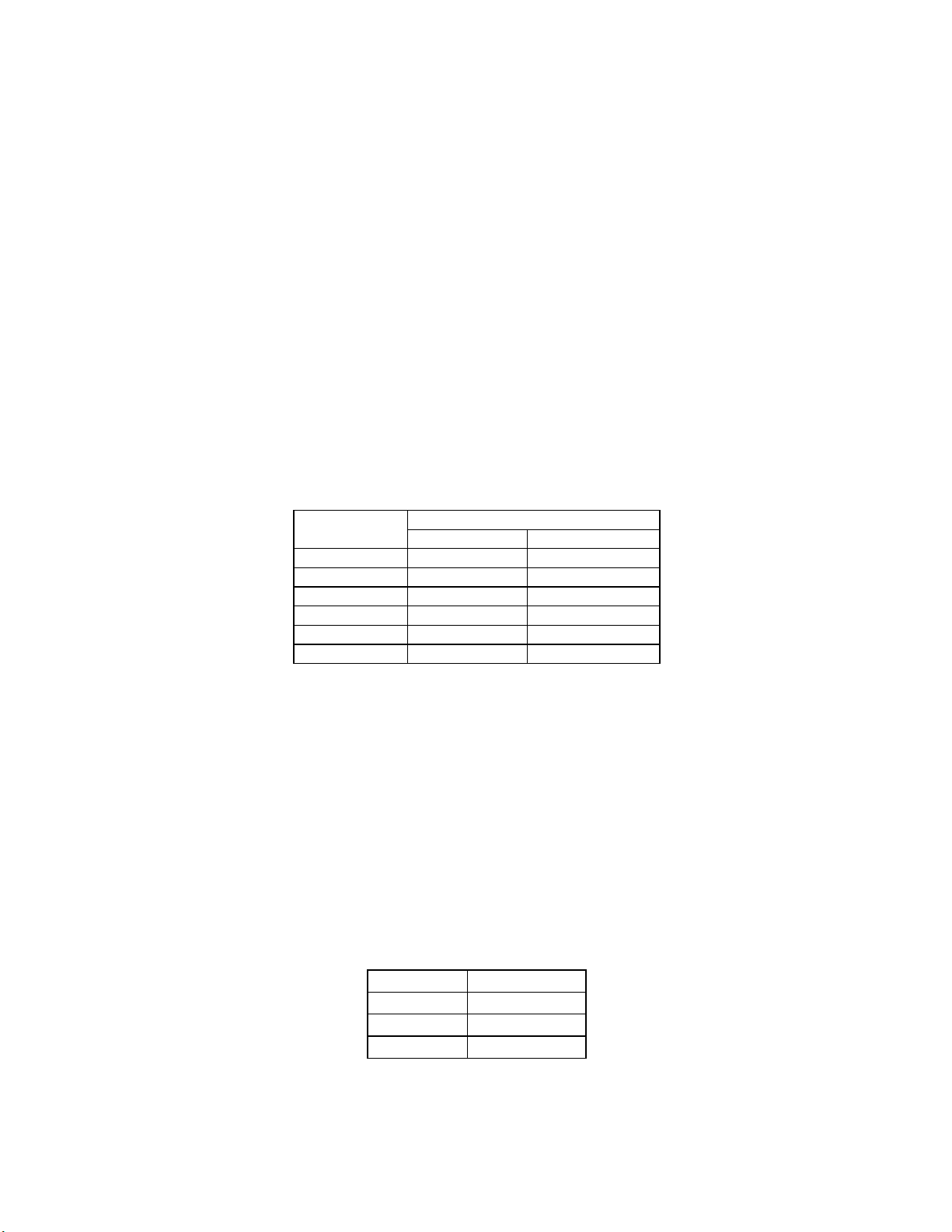
ñưc thông tin v phân phi xác sut ca giá c phiu và tng hp trong bng VI.9.

Bng VI.9. Bng phân phi xác sut giá c phiu

Xác sut ca giá c phiu

Giá c phiu Sau hai tháng Sau bn tháng

42 0,05 0,00

48 0,10 0,05

52 0,15 0,10

56 0,20 0,15

60 0,50 0.30

64 0,00 0,40

Nhà ñ u tư mun xem xét vic mua quyn mua mt s c phiu trong thi hn các

hp ñng trên. Nu giá c phiu trên th trưng chng khoán là cao hơn 48 USD nhà

ñ u tư s, mua vi giá 48 USD/c phiu (ñã mua quyn mua) và bán ngay chúng theo

giá th trưng. Còn nu giá c phiu không vưt quá 48 USD/c phiu trong thi hn

hp ñng thì toàn b s tin mua quyn mua các c phiu s, b tht thu.

Nhà ñ u tư mun la chn mt trong ba phương án sau:

Phương án A: Mua quyn mua 100 c phiu trong hp ñng th nht.

Phương án B: Mua quyn mua 100 c phiu trong hp ñng th hai.

Phương án C: Không mua gì c.

Nhà ñ u tư là ngưi tương ñi bo th, có tính cách “tránh mo him” vi hàm tha

dng ñưc xác ñnh ti mt s mc li nhun như trong bng VI.10.

Bng VI.10. Giá tr hàm th)a dng

Li nhun ð tho dng

1200 1

800 0,8

400 0,7

Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc

………………………………..........182

0 0,6

-400 0,1

-800 0

Xét phương án A, ta có E(u/p

) = 0,05×u(−400) + 0,1×u(−400) + 0,15×u(0) +

0,20×u(400) + 0,50×u(800) + 0×u(1200) = 0,645. Xét phương án B, ta có E(u/p

) =

0×u(−800) + 0,05×u(−800) + 0,1×u(−400) + 0,15×u(0) + 0,30×u(400) + 0,40×u(800) =

0,63. Vi phương án C, E(u/p

) = 0,6.Vy nhà ñ u tư quyt ñnh chn phương án A.

Chú ý: Vic d báo phân phi xác sut ca giá các c phiu cũng là mt vn ñ khá

phc tp, nu các xác sut này chưa bit thì có th coi là chúng bng nhau theo nguyên

lí lí l# không ñ y ñ. Ngoài ra, vi s liu ca ví d trên cũng có th xem xét ñ la

chn nhiu phương án ñ u tư khác.

5. LÍ THUY#T TRÒ CHƠI VÀ )NG DNG

5.1. Mt s! khái nim cơ bn ca lí thuy t trò chơi

2 mc 1, các tiêu chu%n ra quyt ñnh ñã giúp ngưi ra quyt ñnh ñưa ra các la

chn hp lí khi ñi din vi ñi th là môi trưng bt ñnh, không có trí tu.

Trong lí thuyt trò chơi, ta s, hc cách ñưa quyt ñnh khi phi ñi din vi mt hay

nhiu ñi th có trí thông minh. Trong các trò chơi, ñưc hiu theo nghĩa rng, các ñi

th cnh tranh nhau ñu coi là có trí thông minh như nhau, ñu mong mun la chn

cho mình t" mt s h(u hn ho$c vô hn các phương án hành ñng mt phương án hành

ñng hp lí nhm ñt ñưc thành tích tt nht hay li nhun tt nht. Tuy nhiên, lí

thuyt trò chơi, trưc ht là mt lĩnh vc toán hc, không có mc tiêu nghiên cu v

vic làm th nào ñ thng ñưc ñi th, mà tp trung nghiên cu kho sát các mâu thun

ñi kháng khách quan ca trò chơi, nhm gii quyt ñưc vn ñ phát sinh ñng trên

quyn li ca tt c các bên tham gia.

Các ví d ñin hình v lí thuyt trò chơi là v các chin lưc phát trin sn ph%m,

dch v, th trưng trong nn kinh t hàng hóa cnh tranh khu vc và toàn c u, các chin

lưc quân s...

Sau ñây là mt s khái nim cơ bn hay các thut ng( then cht ca lí thuyt trò

chơi:

− ði th gi là ngưi chơi.

− Mt phương án hành ñng ca mt ngưi chơi ñưc gi là mt chin lưc.

− Khi các ñi th ñã la chn các chin lưc hành ñng thì trò chơi cho ta mt kt

cc thưng ñnh lưng bng các s ñưc gi là mt pay-off. Nh(ng t hp chin lưc

khác nhau t" phía các ngưi chơi có th dn ti các kt cc hay các pay-off khác nhau

ca trò chơi.

− Mt trò chơi vi hai ngưi chơi tham gia, mà trong ñó li nhun mà ngưi

này thu ñưc chính bng tht thu ca ngưi kia, ñưc gi là trò chơi hai ngưi -

tng không.

Ví d 1: Hai ngưi chơi A và B tham gia vào trò chơi, m&i ngưi có quyn chn

mt trong hai m$t ca ñng xu: chn m$t có s S (chin lưc 1) ho$c m$t không có

s N (chin lưc 2). Khi ñó có th xy ra các kt cc sau: (S, S) - tc là ngưi th

nht và ngưi th hai ñu chn m$t có s, (S, N) - ngưi th nht chn m$t có s và

ngưi th hai chn m$t không có s, (N, S) và (N, N). Các kt cc này ñưc ñnh

lưng b*i các pay-off: Nu kt cc là (S, S) ho$c (N, N) thì A ñưc coi là thng 1

ñim và B b mt 1 ñim. Còn nu kt cc là (S, N) ho$c (N, S) thì A mt 1 ñim và

B ñưc 1 ñim.

ðây là trò chơi hai ngưi - tng không, vi các d( kin ñưc tng hp b*i ma trn

c 2×2 như sau:

Ngưi chơi B

S N

Ngưi chơi A

1 1

+ −

 

 

− +

 

2 2

 

 



i các pay-off mang d



u + bi



u th



A th



ng (do B thua), còn các pay-off mang d



- bi



u th



anh thua (do B th



ng).

−

Ma tr



n sau

ây

ñư

c g



i là

ma trn trò chơi



a trò ch

i hai ng

ư

i - t



ng không,

khi ng

ư

i ch

i th





t có th





a ch



n hành

ñ

ng theo m



t trong m chi



n l

ư

c t



i m





m, còn ng

ư

i ch

i th



hai có th





a ch



n hành

ñ

ng theo m



t trong n chi



ư

c t



i m

i th





G =

11 12 1n

21 22 2n

m1 m2 mn

a a ... a

... ... ... ...

a a ... a

 

 

 

= ij

m n

 

 

trong

ó a

là pay-off khi ng

ư

i th





t ch

i chi



n l

ư

c i còn ng

ư

i th



hai ch

chi



n l

ư

c j c



a mình. a

có d



u + n



u ng

ư

i th





t th



ng và có d



u - n



u ng

ư

i th





t thua. Không làm gi



m tính t



ng quát, ta gi



trong ma tr



n trò ch

i G không có

hai hàng hay hai c



t gi



ng h



t nhau.

−



u a

≥

∀

j = 1, 2,..., n, k

≠

s và có ít nh



t m



t ch





j* sao cho

kj* sj*

a a

thì ta nói

hàng k là tri hơn hàng s

. Lúc

ó có th





hàng s ra kh



i ma tr



n trò ch

G, vì ng

ư

i th





t s

không bao gi



i chi



n l

ư

c s. Còn n



u a

≥

∀

i = 1, 2,...,

Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc

………………………………..........184

n, k

≠

s và có ít nh



t m



t ch





i* sao cho

i*k i*s

a a

thì ta nói

ct k là tri hơn ct s

Lúc

ó có th







t k ra kh



i ma tr



n trò ch

i G, vì ng

ư

i th



hai s

không bao gi



i chi



n l

ư

c k.

Ví d 2: Xét trò chơi hai ngưi - tng không cho b*i ma trn trò chơi sau

Ngưi chơi B

Ngưi chơi A

8 2 9

6 5 7

3 2 6

7 3 4





−



−







Lúc ñó, có th gch b hàng 3 ra khi ma trn trò chơi, sau ñó ct 4 ra khi ma trn

trò chơi ñ rút gn ma trn trên.

5.2. Trò chơi hai ngư(i - t6ng không vi chi n lưc thu<n nh't

Ví d 3: Xét trò chơi hai ngưi - tng không cho b*i ma trn trò chơi sau

Ngưi chơi B

Ngưi chơi A

8 2 9

6 5 7

7 3 4





−









Gii thích: Trong ma trn trò chơi trên a

= 8, tc là nu A chơi chin lưc 1 ca

mình và B chơi chin lưc 1 ca mình thì A thng 8 còn B thua 8 (ñơn v). Các pay-off

khác ñưc gii thích tương t. 2 ñây, m = 3 và n = 4.

Ta thy nu A chơi chin lưc 1 ca mình thì B s, chơi chin lưc 2 ñ gim thiu

ti ña li nhun ca A và tht thu ca B vi pay - off tương ng là

j 1

Min

} = 2. Nu A

chơi chin lưc 2 thì vi lí do tương t B chơi chin lưc 2 ñ có pay - off là

j 1

Min

}

= 5. còn nu A chơi chin lưc 3 thì B chơi chin lưc 3 dn ti pay - off là

j 1

Min

} =

-4. Do ñó ñ li nhun là ln nht có th, A phi thc hin quy t$c Maximin như sau:

Chn chin lưc k ng vi a

i 1

Max

{

j 1

Min

}} =

i 1

Max

{2, 5, -4} = 5 = a

Như vy A la chn chin lưc 2. Chin lưc này ñưc gi là chin lưc Maximin.

V phía ngưi chơi B, bng lp lun tương t, ñ tht thu là ít nht có th, phi thc

hin quy t$c Minimax như sau:

Các mô hình mạng 9

Tham khảo tài liệu 'các mô hình mạng 9', công nghệ thông tin, quản trị mạng phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi