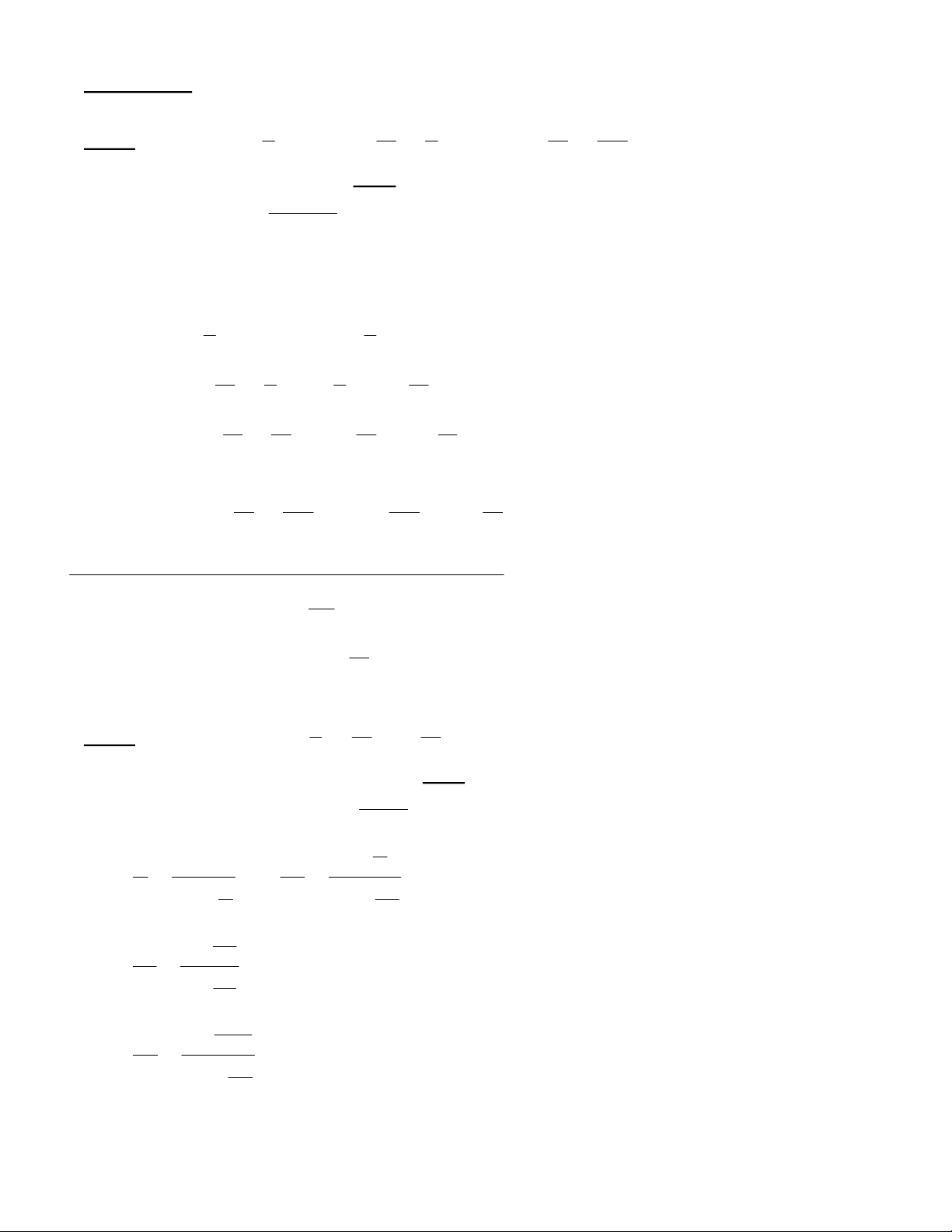
2
CHƯƠNGI:
BIẾNĐỔILƯỢNGGIÁC
Bài1:Cho2 2 1 2
2 1
tan tan 2 tan tan ... 2 tan tan
2 2 2 2 2
n
n n n
a a a a a
S a -
-
= + + +.Tìmlimn
n S
®¥
Giải:
Tacó2
2 tan
tan 2 1 tan
x
x x
= -
2
tan 2 tan 2 tan 2 tanx x x x Û - =
2
tan tan 2 tan 2 2tanx x x x Û = -(1)
Thayvào(1)rồicộngvếtheovế,ta được:
2
2 2
2 2
2 2 2 3
3 2 2 3
1 2 1
1 1
tan tan tan 2 tan
2 2
2 tan tan 2 tan 2 tan
2 2 2 2
2 tan tan 2 tan 2 tan
2 2 2 2
..........................................................
2 tan tan 2 tan 2 tan
2 2 2 2
n n n
n n n n
a a
a a
a a a a
a a a a
a a a a
- -
- -
ì = -
ï
ï
ï = -
ï
ï
ï
+ = -
í
ï
ï
ï
ï = -
ï
ï
î
ta n 2 ta n 2
n
n n
a
S a = -
lim tan lim 2 tan2
n
n n
n n
a
S a
®¥ ®¥
æ ö
Þ = - ç ÷
è ø
tan
n
S a a = -
Bài2: Cho2
cos cos ....cos
2 2 2
n n
x x x
P =.Tìmlimn
n P
®¥
Giải:
Từsin 2
sin 2 2sin cos cos 2sin
a
a a a a a
= Þ =
2
2
2
3
3
1
sin
sin 2
co s , co s
2 2
2 s in 2 sin
2 2
sin 2
co s , ........................
2 sin 2
s in 2
c o s 2 2 sin 2
n
n
n
x
x x x
x x
x
x
x
x
x
x
-
ì
ï = =
ï
ï
ï
ï
ï
ï =
í
ï
ï
ï
ï
ï =
ï
ï
î
3
Nhânvếtheovếtađược:sin
2 sin2
n n
n
x
P x
=
Þsin
lim lim
2 sin2
n
n n n
n
x
P x
®¥ ®¥
=
sin
lim
sin2
2
n
n
n
x
x
x
x
®¥
= æ ö
ç ÷
ç ÷
ç ÷
è ø
=sin x
x
Bài3:Rútgọnbiểuthức:
2 2 2 ....... 2
n
n
A = + + +
14444244443
Giải:
Tacóvớin=1:
1 2 2cos4
A
p
= =
Tasẽchứngminh:2cos2
n n
A
p
=(*)
Vớin=1,đẳngthứcđúng
Giảsử(*)đúngtớin=k,tứclà:
2cos2
k k
A
p
=
Tachứngminh(*)đúngvớin=k+1,tứclà
1 1
2cos2
k k
A
p
+ +
=
Thậtvậy:
1
1
2 2 .... 2
k
k
A +
+
= + +
1442443
2k
A = +
=2(cos2 cos2
k
p
p
+
1 1
4cos( )cos( )
2 2
k k
p p
p p
+ +
= + -
1
2cos2
k
p
+
=(đpcm)
Vậytheonguyênlíquynạp,tacó :
2cos2
n n
A
p
=
4
Bài4: Chovài(hoặctấtcả)cácsố1 2 3
, , ,.....,n
a a a a bằng+1vàcácsốcònlạicủachúngbằng1.
Chứngtỏrằng:
1 2 3 1 2 3
1 2
1 2 1
1 2 3
...
2sin .... 45
2 2 2
2 2 2 ... 2
n
n
n
a a a a a a aa a
a
a a a a
-
æ ö
+ + + +
ç ÷
è ø
= + + + +
o
Chẳnghạnvới1 2 3 ..... 1
n
a a a a = = = = =tađược:
1 1
1 1 1 45
2sin(1 .... )45 2cos 2 2 .... 2
2 4 2 2
n n
n
- -
+ + + + = = + +
o
o 1442443
Giải:
Tasẽtiếnhànhtừcôngthứcnửagóc:
2sin 2 2cos
2
a a
= ± -trongđódấu“+”hoặc”–“đượcchọnchophùhợpvớiquiluậtvề
dấucủahàmsin.Sửdụngcôngthứcnàytalầnlượtđịnhđượcsincácgóc:
1 2 3 1 2 3 1 2 3
1 2 1 2 1 2
1 1 1 1
2 2 1
...
45 ; 45 ; 45 ;.....; .... 45
2 2 2 2 2 2
n
n
a a a a a a a a a a
a a a a a a
a a a a -
æ ö æ ö
æ ö
+ + + + + + +
ç ÷ ç ÷ ç ÷
è ø è ø è ø
o o o o
Giảsửtađãxácđịnhđượcsingóc:
1 2 3 1 2 3
1 2
1 2 1
...
.... 45
2 2 2
n
n
a a a a a a a
a a
a -
æ ö
+ + + +
ç ÷
è ø
otrongđó1 2 3
, , ,.....,n
a a a a lấycácgiátrịbằng+1hoặc1bởi
vì:
1 2 3 1 2 3
1 2
1 2 1
...
2 .... 45
2 2 2
n
n
a a a a a a a
a a
a -
æ ö
+ + + +
ç ÷
è ø
o
=1 2 3 1 2 3
1 2
1 2 1
...
90 .... 45
2 2 2
n
n
a a a a a a aa a
a -
é ù
æ ö
± ± + + + +
ç ÷
ê ú
è ø
ë û
o otrongđódấu“+”tươngứngvớia=1vàdấu”–
“ứmgvớia=1
Và
1 2 3 1 2 3
1 2
1 2 1
...
cos 90 .... 45
2 2 2
n
n
a a a a a a aa a
a -
é ù
æ ö
± ± + + + +
ç ÷
ê ú
è ø
ë û
o o
1 2 3 1 2 3
1 2
1 2 1
...
sin .... 45
2 2 2
n
n
a a a a a a a
a a
a -
æ ö
= - + + + +
ç ÷
è ø
o
Ápdụngcôngthức2sin 2 2cos
2
a
= ± -, tacó:
1 2 3 1 2 3
1 2
1 2 1
...
2sin .... 45
2 2 2
n
n
a a a a a a a
a a
a -
æ ö
+ + + +
ç ÷
è ø
o
1 2 3 1 2 31 2
1 2 1
...
2 2sin .... 45
2 2 2
n
n
a a a a a a aa a
a -
æ ö
= ± + + + + +
ç ÷
è ø
o
Để ý rằng tất cả các góc được xét đều nhỏ hơn90
ovề mặt giá trị tuyệt đối ( ngay cả
2
1 1 1 1
1 ... 45 90 90 90
2 2 2 2
n n
æ ö
+ + + + = - <
ç ÷
è ø
o o o ovàvìdấucủacácgócnàyđượcđịnhbởidấucủa1
a ,nên
cănbậchaitrongcôngthứccuốiphảilấydấu“+”hoặc”–“tùytheodấucủa1
a .Nóicáchkhácta
cóthểviết:
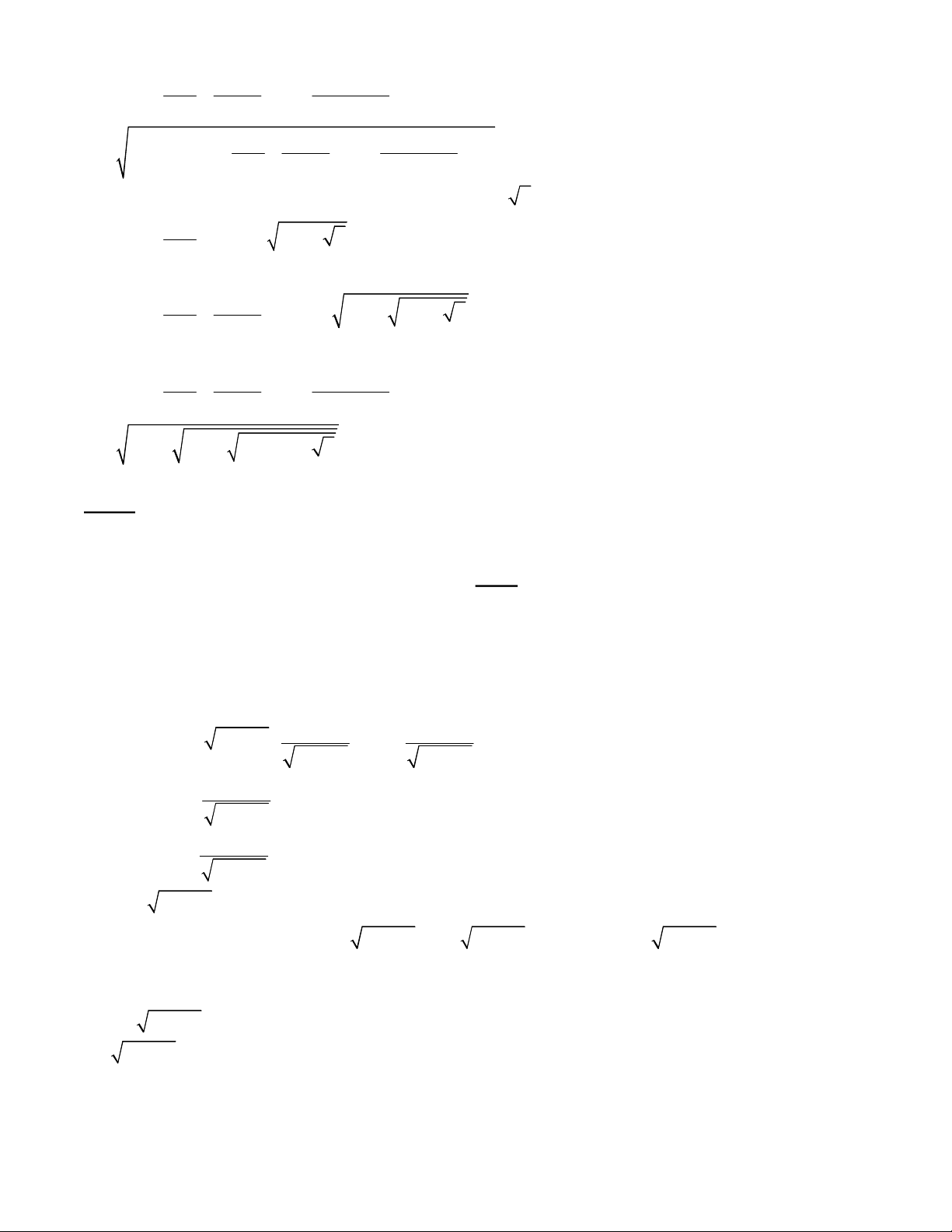
5
1 2 3 1 2 3
1 2
1 2 1
...
2sin .... 45
2 2 2
n
n
a a a a a a a
a a
a -
æ ö
+ + + +
ç ÷
è ø
o
1 2 3 1 2 31 2
1 1 2 1
...
2 2sin .... 45
2 2 2
n
n
a a a a a a aa a
a a -
æ ö
= + + + + +
ç ÷
è ø
o
Giờtahãydùngcôngthứchiểnnhiên1 1
2sin 45 2a a =
ogiúptasuyraliêntiếpcáchệthứcsau:
1 2
1 1 2
2sin 45 2 2
2
a a
a a a
æ ö
+ = +
ç ÷
è ø
o
1 2 3
1 2
1 1 2 3
2
2sin 45 2 2 2
2 2
a a a
a a
a a a a
æ ö
+ + = + +
ç ÷
è ø
o
……………………………………………
1 2 3 1 2 3
1 2
1 2 1
1 2 3
...
2sin .... 45
2 2 2
2 2 2 ... 2
n
n
n
a a a a a a aa a
a
a a a a
-
æ ö
+ + + +
ç ÷
è ø
= + + + +
o
Bài5:Tìmđiềukiệnđốivớiavàbđểhàmsố:
2 sin cosy x a x b x = + +luônđồngbiến
Giải:
Hàmsốcótậpxácđịnh D R =
Cóđạohàm' 2 cos siny a x b x = + -
Trườnghợp1:0 ' 2 0a b y = = Þ = >x R " Î
Điềunàythỏamãnyêucầuđề bài
Trườnghợp2:2 2 0a b + >
Tacó:2 2
2 2 2 2
' 2 cos sin
a b
y a b x x
a b a b
æ ö
= + + -
ç ÷
+ +
è ø
Với2 2
2 2
cos
sin
a
a b
b
a b
j
j
ì =
ï +
ï
í
ï =
ï +
î
( )
2 2
' 2 cosy a b x
j
= + + +
vì
( )
1 cos 1x
j
- £ + £nên
( )
2 2 2 2 2 2
2 2 cos 2a b a b x a b
j
Û - + £ + + + £ + +
Đểhàmsốluônđồngbiến:
' 0y Û ³x R " Î
2 2
2 0a b Û - + ³
2 2 2a b Û + £
2 2 4a b Û + £
Kếiluận2 2 4a b + £
(chúý2 2 4a b + £vẫnđúngkhi0a b = =)
6
Bài6:
Chohàmsố3
4y x mx = -.Tínhmđể1y £khi1x £
Giải:
Thuận:vì1x £nêntachọn:
*1 4x y m = Þ = -
Theogiả thiết1y £ 4 1m Þ - £
Þ1 4 1m - £ - £
Þ3 5m £ £(1)
Theogiảthiết1
2
1
1 £
-
Þ £m
y
31
212
21
£ £ - Þ
£ - £ - Þ
£ - Þ
m
m
m
Kếthợp(1)và(2)suyram=3
Đảo:vớim=3 xxy 34 3 - = Þ
Theogiảthiết1 £x
a a
cos: = Î $ Û xR
Vậy
a a
cos3cos4 3 - =y
13cos
3cos
£ = Û
= Û
a
a
y
y
Kếtluậnm=3
Bài7:Chứngminhrằngnếu)cos()sin( baam = = +trongđo
p
kba ¹ -và1 ¹m thìbiểuthức
bmam
E2sin1
1
2sin1
1
-
+
-
=khôngphụthuộcvàoavàb
Giải:
Tacó:)]()sin[(2sin babaa - + + =
)sin()cos()(sin
)sin()cos()cos()sin(
2bababam
babababa
- + + + =
- + + - + =
)]cos())[sin(sin(
)sin()cos()(sin
)sin()cos()(cos1
)sin()cos()(sin12sin1
2
2
22
bambaba
babamba
babamba
babambamam
+ - - - =
- + - - =
- + - - - =
- + - + - = - Þ
Tươngtự)]cos())[sin(sin(2sin1 bambababm + + - - = -
1 1
sin( )[sin( ) cos( )] sin( )[sin( ) ( )]
1 1 1
sin( ) sin( ) cos( ) sin( ) cos( )
E a b a b m a b a b a b mco a b
a b a b m a b a b m a b
= +
- - - + - - + +
é ù
= +
ê ú
- - - + - + +
ë û