Bé gi¸o dôc vµ ®µo t¹o kú thi tuyÓn sinh ®¹i häc, cao ®¼ng n¨m 2003
−−−−−−−−−−−−− ®¸p ¸n −thang ®iÓm
®Ò thi chÝnh thøc M«n thi : to¸n Khèi D
Néi dung ®iÓm
C©u 1. 2®iÓm
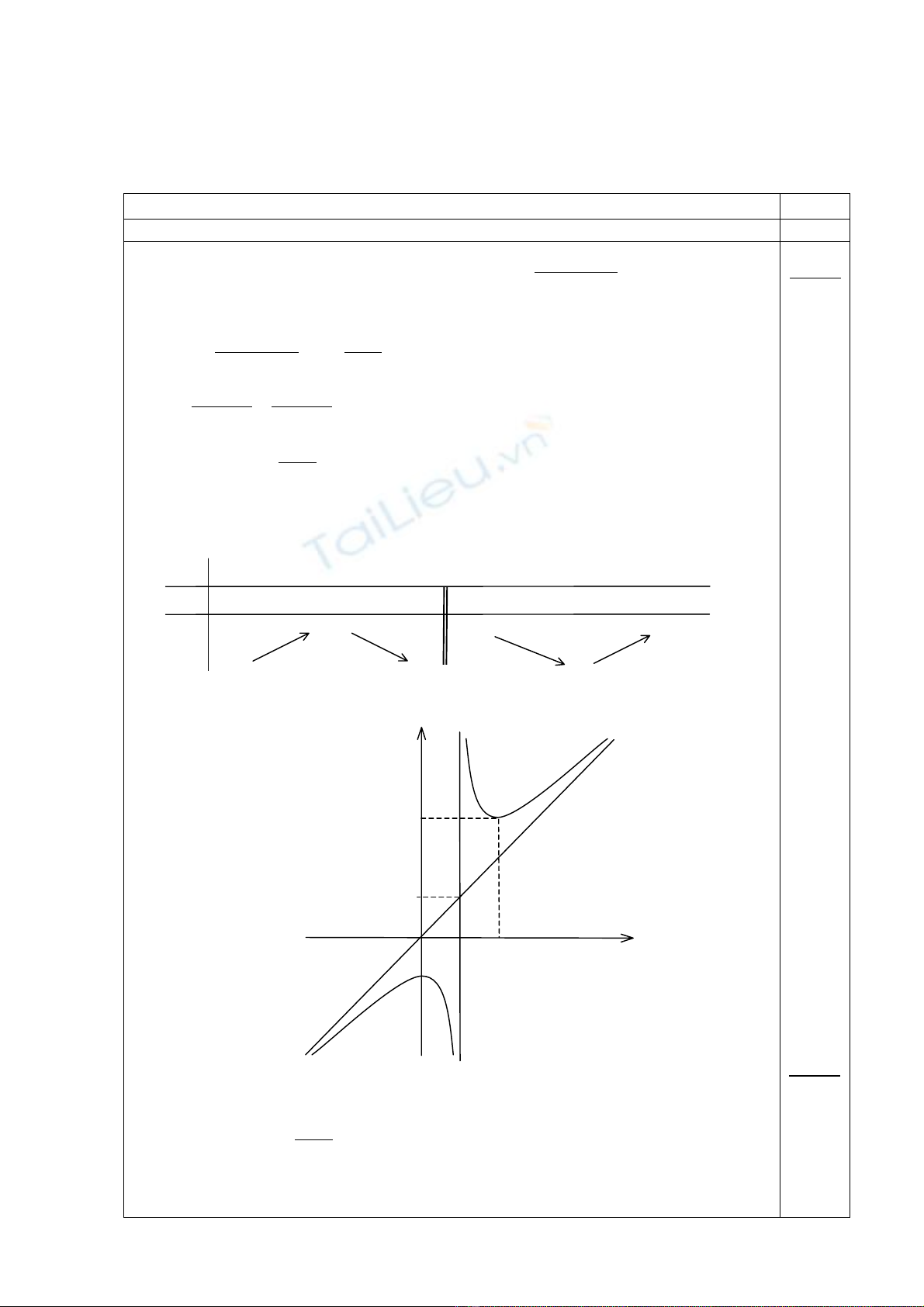
1) Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ cña hµm sè
224
2
xx
yx
−
+
=−. 1 ®iÓm
TËp x¸c ®Þnh : R \{ 2 }.
Ta cã
224 4
.
22
xx
yx
xx
−+
==+
−−
2
22
0
44
' 1 . ' 0 4.
(2) (2)
x
xx
yy
x
xx
=
−
=− = = ⇔
=
−−
[]
4
lim lim 0
2
xx
yx x
→∞ →∞
−= =⇒
− tiÖm cËn xiªn cña ®å thÞ lµ: yx
=
,
tiÖm cËn ®øng cña ®å thÞ lµ:
2
lim
x
y
→=∞⇒ 2x
=
.
B¶ng biÕn thiªn:
§å thÞ kh«ng c¾t trôc hoµnh.
§å thÞ c¾t trôc tung t¹i ®iÓm (0; −2).
0,25®
0,5®
0,25®
2) 1 ®iÓm
§−êng th¼ng c¾t ®å thÞ hµm sè (1) t¹i 2 ®iÓm ph©n biÖt
m
d
⇔ ph−¬ng tr×nh 422
2
x
mx m
x
+=+−
− cã hai nghiÖm ph©n biÖt kh¸c 2
2
( 1)( 2) 4mx⇔− − = cã hai nghiÖm ph©n biÖt kh¸c 2 ⇔ 10m
−
> 1.m
>
VËy gi¸ trÞ cÇn t×m lµ m1.m>
0,5®
0,5®
x
2
6
−
2
2 4O
y
x
−
∞ 0 2 4 + ∞
y
’ + 0 − − 0 +
− 2 + ∞ + ∞
y
C§ CT
−
∞
−
∞ 6
1
C©u 2. 2®iÓm
1) Gi¶i ph−¬ng tr×nh 222
πtg cos 0
24 2
xx
x

−−


sin (1)
=1 ®iÓm
§iÒu kiÖn: (*). Khi ®ã cos 0x≠
()
2
2
1sin1
(1) 1 cos 1 cos
222
cos
x
x
x
x
π


⇔− − =+




() ( )
22
1sin sin 1cos cos
x
xx⇔− =+ x
()
(
)
1 sin (1 cos )(1 cos ) 1 cos (1 sin )(1 sin )
x
xx xx⇔− − + =+ − + x
()
1 sin (1 cos )(sin cos ) 0xxxx⇔− + + =
π2π
sin 1 2
cos 1 π2π
tg 1 ππ
4
x
k
x
x
xk
x
x
k
=+
=
⇔=−⇔=+
=−
=− +
()k
∈
Z.
KÕt hîp ®iÒu kiÖn (*) ta ®−îc nghiÖm cña ph−¬ng tr×nh lµ:
π2π
ππ
4
x
k
x
k
=+
=
−+
(). k∈Z
0,5®
0,25®
0,25®
2) Gi¶i ph−¬ng tr×nh (1).
22
2
22
xx xx−+−
−3=1 ®iÓm
§Æt .
2
20
xx
tt
−
=⇒>
Khi ®ã (1) trë thµnh 2
43340(1)(4)0ttttt
t
−=⇔ −−=⇔+ − =⇔=4t (v× t) 0>
VËy 22
24
xx xx
−=⇔ −=21
2.
=
−
⇔
=
x
x
Do ®ã nghiÖm cña ph−¬ng tr×nh lµ 1
2.
=
−
=
x
x
0,5®
0,5®
C©u 3. 3®iÓm
1) 1 ®iÓm
Tõ () suy ra cã t©m vµ b¸n kÝnh
22
:( 1) ( 2) 4−+− =Cx y ()C(1; 2)I2.R=
§−êng th¼ng cã vÐct¬ ph¸p tuyÕn lµ nd(1; 1).
=
−
u
ur Do ®ã ®−êng th¼ng ∆ ®i qua
vµ vu«ng gãc víi d cã ph−¬ng tr×nh:
(1; 2)I12
11
xy xy
30
−
−
=
⇔+−
−=.
Täa ®é giao ®iÓm cña vµ lµ nghiÖm cña hÖ ph−¬ng tr×nh:
Hd∆
10 2 (2;1).
30 1
xy x H
xy y
−−= =

⇔⇒

+−= =

Gäi lµ ®iÓm ®èi xøng víi qua . Khi ®ã J(1; 2)Id
23(3; 0)
20
JHI
JHI
xxx J
yxx
=−=
⇒
=−=
.
V× ®èi xøng víi ( qua nªn cã t©m lµ vµ b¸n kÝnh
Do ®ã cã ph−¬ng tr×nh lµ:
(')C
(C
)Cd(')C
22
(3;0)J2.R=
') (3) 4
−
+xy=.
Täa ®é c¸c giao ®iÓm cña ( vµ lµ nghiÖm cña hÖ ph−¬ng tr×nh: )C(')C
22
22 2
22
10 1
(1) ( 2) 4 1, 0
3, 2.
(3) 4 2 860
(3) 4
xy yx
xy xy
xy
xy xx
xy
−−= =−

−+− = = =

⇔⇔⇔

==
−+= −+=

−+=

VËy täa ®é giao ®iÓm cña vµ ( lµ vµ ()C')C(1; 0)A(3; 2).B
0,5
0,25®
0,25®
2
2) 1 ®iÓm
Ta cã cÆp vect¬ ph¸p tuyÕn cña hai mÆt ph¼ng x¸c ®Þnh lµ
k
d1(1; 3 ; 1)
=
−
u
ur
nk
vµ . Vect¬ ph¸p tuyÕn cña lµ
2(; 1;1)=−
uur
nk ()P(1; 1; 2)
=
−−
r
n.
§−êng th¼ng cã vect¬ chØ ph−¬ng lµ:
k
d
2
12
,(31;1;13)0 k k k−−−−−≠
r
Nªn
2
1 13 1.
11 2
kk k
k
−−−−−
= = ⇔=
−−
VËy gi¸ trÞ cÇn t×m lµ
0,5®
0,5 ®
3) 1 ®iÓm
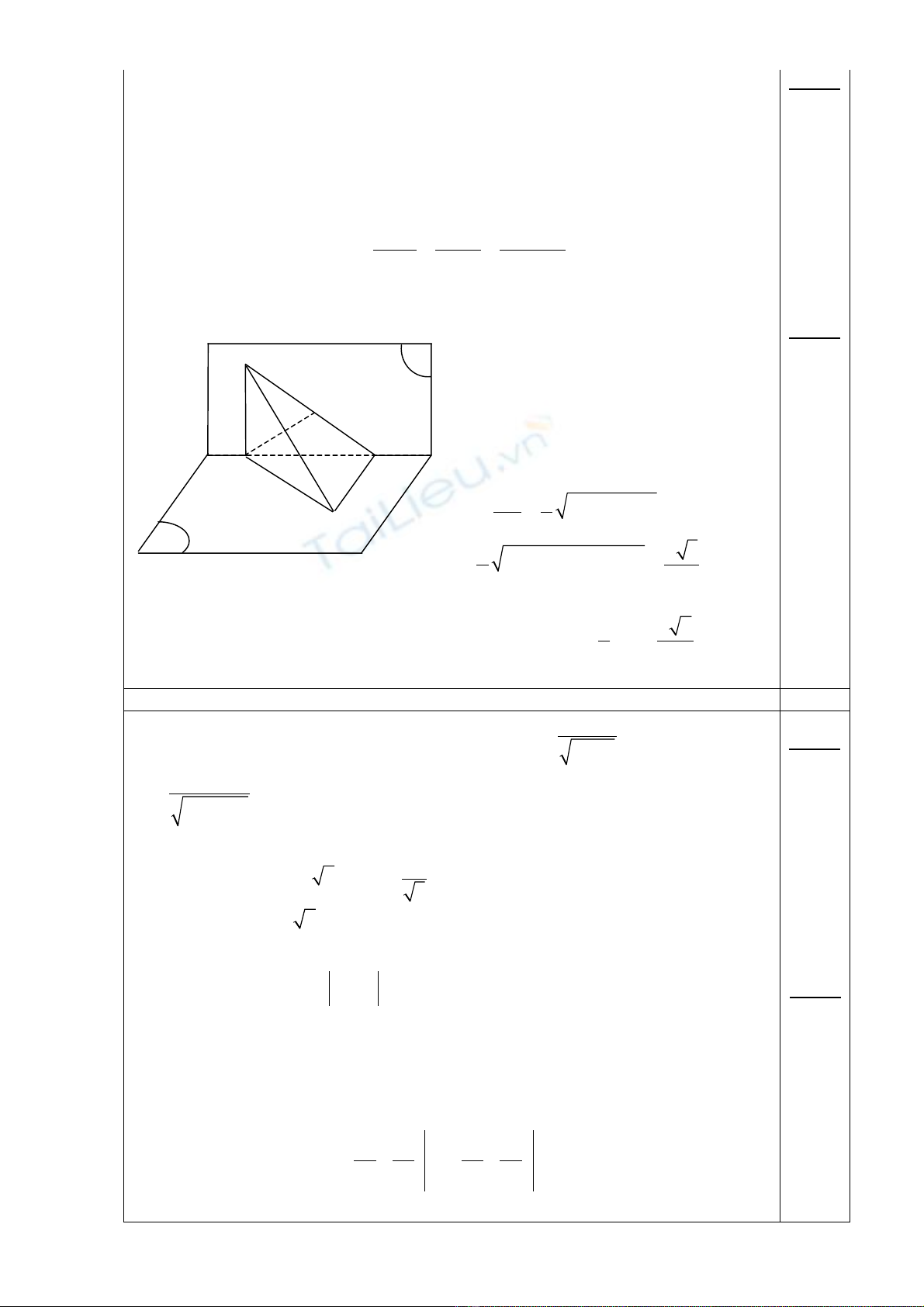
Ta cã (P) ⊥ (Q) vµ ∆ = (P) ∩ (Q), mµ
AC ⊥ ∆ ⇒ AC ⊥(Q) ⇒AC ⊥ AD, hay
. T−¬ng tù, ta cã BD ⊥ ∆ nªn
BD ⊥(P), do ®ã CBD . VËy A vµ B
A, B n»m trªn mÆt cÇu ®−êng kÝnh CD.
0
90=CAD
0
90=
Vµ b¸n kÝnh cña mÆt cÇu lµ:
22
1
22
CD
R
BC BD== +
222
13
22
a
AB AC BD=++=.
Gäi H lµ trung ®iÓm cña BC⇒ AH ⊥ BC. Do BD ⊥(P) nªn BD ⊥ AH ⇒AH ⊥ (BCD).
VËy AH lµ kho¶ng c¸ch tõ A ®Õn mÆt ph¼ng (BCD) vµ 12
.
22
a
AH BC==
0,25®
0,25®
0,5®
C©u 4. 2®iÓm
1) T×m gi¸ trÞ lín nhÊt vµ gi¸ trÞ nhá nhÊt cña hµm sè 2
1
1
x
y
x
+
=
+
trªn ®o¹n
[
]
1; 2−. 1 ®iÓm
23
1
'.
(1)
x
y
x
−
=
+
'0 1yx=⇔=.
Ta cã 3
(1) 0, 2, (2) .
5
y(1) yy−= = =
VËy
[]
1; 2
(1) 2max yy
−== vµ
[]
1; 2
min ( 1) 0.yy
−
=
−=
0,5®
0,5®
2) TÝnh tÝch ph©n
2
2
0
I
xxd=−
∫x
. 1 ®iÓm
Ta cã 200 1
x
xx−≤ ⇔ ≤≤, suy ra
12
22
01
() () =− + −
∫∫
I
x x dx x x dx
12
23 32
01
1.
23 32

=− +− =



xx xx
0,5®
0,5®
unn k

==

r
uuruur
31
() || k
dPun⊥⇔ ⇔
rr
k1.=k
.∀
A
B
C
D
P
Q
∆
H
3
C©u 5. 1®iÓm
C¸ch 1: Ta cã (202122224
1) ...
nnn n
nn n n
n
x
Cx Cx Cx C
−−
+= + + ++,
011222333
( 2) 2 2 2 ... 2
nn n n n n
nn n n n
n
x
Cx Cx Cx Cx C
−−−
+= + + + ++ .
DÔ dµng kiÓm tra 1, 2
=
=nn kh«ng tháa m·n ®iÒu kiÖn bµi to¸n.
Víi th× 3≥n33 2 3 22 1
.
nnnnn
xxxxx
−−−
==
−
Do ®ã hÖ sè cña 33
−
n
x trong khai triÓn thµnh ®a thøc cña lµ
2
(1)(2++
nn
xx)
n
C
303 11
33 2. . 2. .
nnnn
aCCC
−=+.
VËy
2
33
5
2(2 3 4)
26 26 7
32
−
=
−+
=⇔ =⇔
=
−
n
n
nn n
an n
n
VËy lµ gi¸ trÞ cÇn t×m (v× nguyªn d−¬ng). 5=n n
C¸ch 2:
Ta cã
23
2
332
2
00 00
12
(1)(2) 1 1
12 2.
nn
nnn
ik
nn nn
ni k niikkk
nn nn
ik ik
xx x x
x
xC C xCxCx
x
x
−−
== ==


++= + +





 

==






∑∑ ∑∑
Trong khai triÓn trªn, luü thõa cña
x
lµ 33n
−
khi 23ik
−
−=−
3k
, hay
Ta chØ cã hai tr−êng hîp tháa ®iÒu kiÖn nµy lµ
23ik+=.
0,i
= hoÆc i1, 1k
=
=.
Nªn hÖ sè cña 33
−
n
x lµ .
033 11
33 ..2 ..2
nnn nn
aCCCC
−=+
Do ®ã
2
33
5
2(2 3 4)
26 26 7
32
−
=
−+
=⇔ =⇔
=
−
n
n
nn n
an n
n
VËy lµ gi¸ trÞ cÇn t×m (v× nguyªn d−¬ng). 5=n n
0,75®
0,25®
hoÆc
0,75®
0,25®
4