1
Bé gi¸o dôc vµ ®µo t¹o §¸p ¸n - thang ®iÓm
§Ò chÝnh thøc §Ò thi tuyÓn sinh ®¹i häc, cao ®¼ng n¨m 2004
M«n: VËt lÝ , Khèi A
(§¸p ¸n - thang ®iÓm cã 3 trang)
C©u ý Néi dung §iÓm
1 ®iÓm I
Ph−¬ng tr×nh ph©n r·: NieCo 60
28
0
1
60
27 +→ −
− . . . . . . . . . . . . . . . . . . . .
H¹t nh©n Ni cã 28 pr«t«n vµ 32 n¬tr«n. . . . . . . . . . . . . . . . . . . . .
L−îng chÊt phãng x¹ cßn l¹i so víi ban ®Çu: 100% - 75% = 25%
§Þnh luËt phãng x¹: T
t
0
t
T
2ln
0
t
02mememm −−
λ− === . . . . . . . . . . . . . . . . . . . .
⇒== 4
m
m
20
T
t
t = 2T = 10,54 n¨m . . . . . . . . . . . . . . . . . . . .
0,25
0,25
0,25
0,25
2 ®iÓm
1
Kho¶ng c¸ch gi÷a 2 v©n s¸ng liªn tiÕp (kho¶ng v©n): i = 2 mm . . . . . . . . . . . . . . . . .
B−íc sãng ¸nh s¸ng m64,0
D
ai µ==λ . . . . . . . . . . . . . . .
V©n tèi thø 3 n»m gi÷a v©n s¸ng thø 2 vµ thø 3 . . . . . . . . . . . . .
VÞ trÝ cña v©n tèi thø ba: xt3 = ± 2,5i = ± 5 mm . . . . . . . . . .
1 ®iÓm
0,25
0,25
0,25
0,25
II
2
B−íc sãng 1
λ
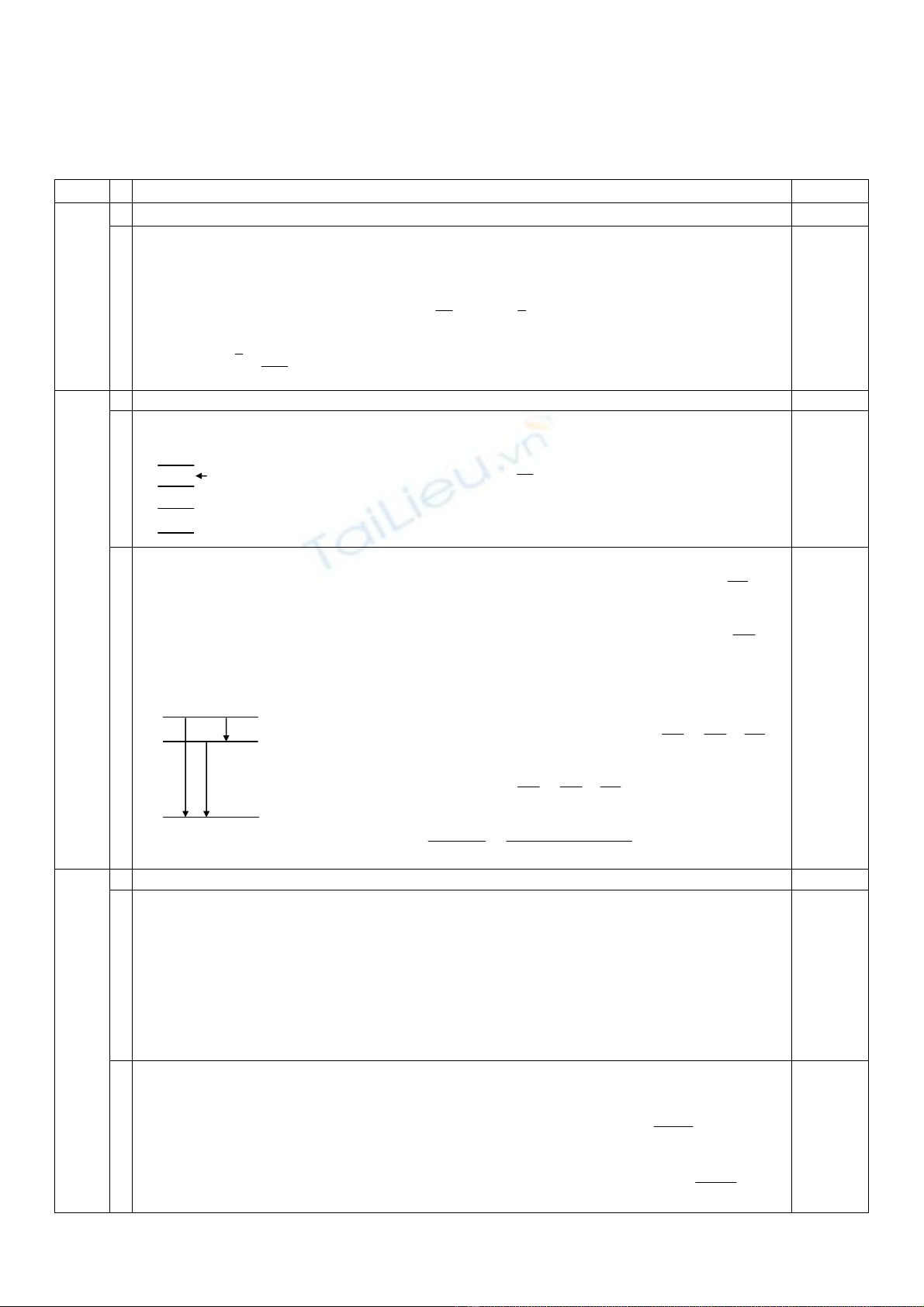
øng víi sù chuyÓn cña ªlectr«n tõ quÜ ®¹o L vÒ quÜ ®¹o K:
1
KL
hc
EE λ
=− (1)
B−íc sãng 2
λøng víi sù chuyÓn cña ªlectr«n tõ quÜ ®¹o M vÒ quÜ ®¹o K:
2
KM
hc
EE λ
=− (2)
B−íc sãng dµi nhÊt 3
λtrong d·y Banme øng víi sù chuyÓn cña ªlªctr«n tõ quÜ ®¹o M vÒ quÜ
®¹o L.
Tõ (1) vµ (2) (hoÆc tõ h×nh vÏ) suy ra:
123
LM
hchchc
EE λ
−
λ
=
λ
=−
⇒
123
111
λ
−
λ
=
λ
m6566,0
1026,01216,0
)1026,0)(1216,0(
21
21
3µ=
−
=
λ−λ
λλ
=λ⇒ . . . . .
1 ®iÓm
0,25
0,25
0,25
0,25
2 ®iÓm III
1
- TÇn sè cña dao ®éng tù do chØ phô thuéc vµo ®Æc tÝnh cña hÖ, cßn tÇn sè cña dao ®éng c−ìng
bøc b»ng tÇn sè cña ngo¹i lùc. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- Biªn ®é cña dao ®éng tù do phô thuéc vµo c¸ch kÝch thÝch ban ®Çu, cßn biªn ®é cña dao
®éng c−ìng bøc phô thuéc vµo quan hÖ gi÷a tÇn sè cña ngo¹i lùc vµ tÇn sè dao ®éng riªng cña
hÖ. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- HiÖn t−îng ®Æc biÖt cã thÓ x¶y ra trong dao ®éng c−ìng bøc lµ hiÖn t−îng céng h−ëng. . . . .
- §iÒu kiÖn x¶y ra hiÖn t−îng céng h−ëng lµ tÇn sè cña ngo¹i lùc c−ìng bøc b»ng tÇn sè dao
®éng riªng cña hÖ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1 ®iÓm
0,25
0,25
0,25
0,25
2
XÐt ®iÓm M trªn mÆt chÊt láng c¸ch S1 mét kho¶ng d1 vµ c¸ch S2 mét kho¶ng d2.
Ph−¬ng tr×nh dao ®éng t¹i M do nguån S1 truyÒn tíi: ⎟
⎠
⎞
⎜
⎝
⎛
λ
π
−π= 1
M1
d2
t50sin2,0u cm . . . .
Ph−¬ng tr×nh dao ®éng t¹i M do nguån S2 truyÒn tíi: ⎟
⎠
⎞
⎜
⎝
⎛
λ
π
−π+π= 2
M2
d2
t50sin2,0u cm
1 ®iÓm
0,25
0
3
2
1
i
v©n tèi thø 3
M
L
K
hc/λ2 hc/λ1
hc/λ3
2
Ph−¬ng tr×nh dao ®éng tæng hîp t¹i M: uM = u1M + u2M
() ()
⎥
⎦
⎤
⎢
⎣
⎡π
+
λ
+π
−π
⎥
⎦
⎤
⎢
⎣
⎡π
−
λ
−π
=2
dd
t50sin
2
dd
cos4,0u 2112
M cm . . . . . . . . . . . . .
Tõ ph−¬ng tr×nh trªn ta thÊy nh÷ng ®iÓm cã biªn ®é dao ®éng cùc ®¹i (0,4 cm) tho¶ m·n ®iÒu
kiÖn:
() () ()
2
1k2ddk
2
dd
1
2
dd
cos 12
1212 λ
+=−⇒π=
⎥
⎦
⎤
⎢
⎣
⎡π
−
λ
−π
⇒±=
⎥
⎦
⎤
⎢
⎣
⎡π
−
λ
−π
Tõ ®Çu bµi tÝnh ®−îc: Hz25
2
f=
π
ω
=, cm2
f
v==λ
C¸c ®iÓm n»m trªn ®o¹n th¼ng S1S2 cã biªn ®é cùc ®¹i ph¶i tháa m·n c¸c ph−¬ng tr×nh sau:
()
2
1k2dd 12
λ
+=− = 2k + 1 (1) . . . . . . . .
d2 + d1 = S1S2 = 10 (2)
Tõ (1) vµ (2) suy ra: d1 = 4,5 – k
V× 0 ≤ d1 ≤ 10 nªn - 5,5 ≤ k ≤ 4,5
⇒ k = - 5, - 4, ...., 0, 1, .... 4
Cã 10 ®iÓm dao ®éng víi biªn ®é cùc ®¹i. . . . . . . .
0,25
0,25
0,25
2 ®iÓm
1
TÇn sè dao ®éng:
()
F5F10.5
10.5010.2
1
L
1
C
LC
16
3
2
3
2µ===
ω
=⇒=ω −
− . . . . . .
N¨ng l−îng dao ®éng ®iÖn tõ trong m¹ch: 222
00 Cu
2
1
Li
2
1
LI
2
1
W+== . . . . . . . . . . .
Khi 2
0
2
0
2
0
2
0LI
4
1
2
I
IL
2
1
Cu
2
1
2
I
Ii =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=⇒== . . . . . . . . . .
V24
C2
L
Iu 0==⇒≈ 5,66 V . . . . . . . . . . .
1 ®iÓm
0,25
0,25
0,25
0,25
IV
2
V× i sím pha h¬n uAB nªn trong hép X cã tô ®iÖn C . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C«ng suÊt tiªu thô trªn ®o¹n m¹ch: P = I2R =
R
Z
R
U
ZR
RU
2
C
2
2
C
2
2
+
=
+ . . . . . . . . . . .
§Ó P ®¹t cùc ®¹i th× mÉu sè ph¶i cùc tiÓu. Tõ bÊt ®¼ng thøc C«si ⇒ R = ZC (1) . . .
MÆt kh¸c Ω===+= 2100
2
200
I
U
ZRZ 2
C
2
AB (2)
⇒ ZC = 100 Ω⇒ C = F10.
1
Z.f2
1
Z
14
CC
−
π
=
π
=
ω ≈ 31,8 µF . . . . . . . . .
1 ®iÓm
0,25
0,25
0,25
0,25
V
3 ®iÓm
1
Khi ®eo kÝnh, ng−êi ®ã nh×n ¶nh ¶o cña vËt qua kÝnh.
VËt c¸ch m¾t (nghÜa lµ c¸ch kÝnh) kho¶ng ng¾n nhÊt d = 25 cm th× ¶nh ë ®iÓm cùc cËn cña
m¾t, c¸ch m¾t 50 cm. Do ¶nh lµ ¶o nªn d’ = - 50 cm. . . . . . . . . . . . . . . . . . . . . .
C«ng thøc thÊu kÝnh: '
d
1
d
1
f
1+= . . . . . . . . . . . . . . . . . . . . . .
⇒ cm50
'
d
d
'dd
f=
+
= . . . . . . . . . . . . . . . . . . . .
§é tô cña kÝnh: 2
5,0
1
f
1
D=== ®ièp . . . . . . . . . . . . . . . . . . . .
1 ®iÓm
0,25
0,25
0,25
0,25
3
2
a) TÝnh f vµ AB
Do ¶nh A1B1 høng ®−îc trªn mµn nªn ®©y lµ ¶nh thËt vµ thÊu kÝnh lµ thÊu kÝnh héi tô. . . . . .
Khi cã ¶nh A1B1 ta cã '
1
1d
1
d
1
f
1+= (1)
Khi cã ¶nh A2B2 ta cã '
2
2d
1
d
1
f
1+= (2)
DÞch thÊu kÝnh ra ra vËt 5 cm: d2 = d1 + 5 (3)
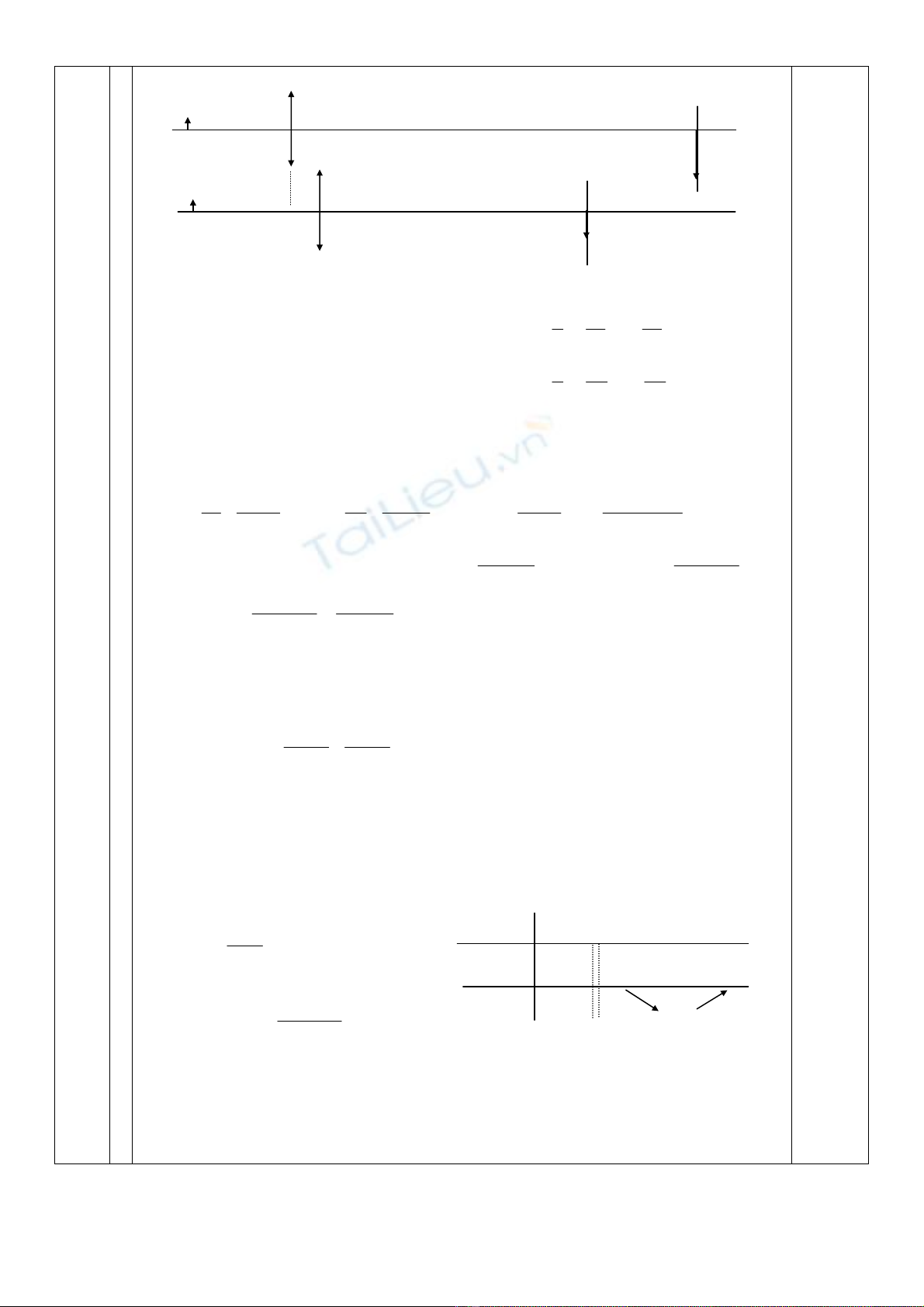
NÕu dÞch mµn ra xa vËt mµ cã ¶nh trªn mµn th× d2’ = d1’ + 30, kh«ng tho¶ m·n (1) vµ (2).
VËy ph¶i dÞch chuyÓn mµn l¹i gÇn vËt (h×nh vÏ): d2’ = d1’ – 40 (4)
MÆt kh¸c A1B1 = 2A2B2 nªn k1 = 2k2.
22
'
2
2
11
'
1
1df
f
d
d
k,
df
f
d
d
k−
=−=
−
=−= ⇒ )5d(f
f
.2
df
f
11 +−
=
− (5)
Tõ (5) ⇒ d1 = f + 5, d2 = f + 10 ; tõ (1) ⇒ 5
f)5f(
d'
1
+
=; tõ (2) ⇒ 10
f)10f(
d'
2
+
=
Thay vµo (4):
()
40
5
f5f
10
f)10f( −
+
=
+ ⇒ f = - 20 cm (lo¹i) vµ f = 20 cm . . . .
d1 = f + 5 = 25 cm ⇒ k1 = - 4 ⇒ AB = 1 cm . . . .
b) T×m ®é dÞch chuyÓn cña thÊu kÝnh
Theo trªn, khi cã d2 = 30 cm th× d2’ = 60cm.
Kho¶ng c¸ch tõ AB ®Õn mµn khi cã ¶nh A2B2 lµ: L0 = d2 + d2’ = 90 cm
L0 = fd
d
fd
fd
d
2
2
2
2
2
2−
=
−
+ ⇒ 0fLdLd 020
2
2=+− . . . . . . . . . . .
Víi L0 = 90 cm, f = 20 cm ta cã: 01800d90d 2
2
2=+−
Ph−¬ng tr×nh cã 2 nghiÖm:
d21 = 30 cm (®ã lµ vÞ trÝ cña thÊu kÝnh trong tr−êng hîp c©u a)
d22 = 60 cm (®ã lµ vÞ trÝ thø 2 cña thÊu kÝnh còng cã ¶nh trªn mµn)
§Ó l¹i cã ¶nh râ nÐt trªn mµn, ph¶i dÞch thÊu kÝnh vÒ phÝa mµn 30 cm. . . . . . . . . . . .
XÐt sù dÞch chuyÓn cña ¶nh
Kho¶ng c¸ch gi÷a vËt vµ ¶nh thËt:
fd
d
'ddL
2
−
=+= (chØ xÐt d > f)
Kh¶o s¸t sù thay ®æi cña L theo d:
Ta cã ®¹o hµm
()
2
2
fd
df2d
'L −
−
= = 0
khi d = 0 (lo¹i) vµ d = 2f.
Tõ b¶ng biÕn thiªn thÊy khi d = 2f = 40 cm th× kho¶ng c¸ch gi÷a vËt vµ ¶nh cã mét gi¸ trÞ cùc
tiÓu Lmin = 4f = 80 cm < 90 cm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nh− vËy, trong khi dÞch chuyÓn thÊu kÝnh tõ vÞ trÝ d21 = 30 cm ®Õn d22 = 60 cm th× ¶nh cña vËt
dÞch chuyÓn tõ mµn vÒ phÝa vËt ®Õn vÞ trÝ gÇn nhÊt c¸ch vËt 80 cm råi quay trë l¹i mµn. . . .
2 ®iÓm
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
d f 2f
L’ - 0 +
L
Lmi
n
= 4
B1
A A1
O
d1 d1’
B
A
B O
A2
B2
d2' = d1’ - 40
d2 = d1 + 5
5cm 35cm