ÑEÀ THI & BAØI GIAÛI THI ÑH 2006
MOÂN TOAÙN KHOÁI B
Caâu I: (2 ñieåm)
Cho haøm soá y =
2
xx1
x2
+−
+
1. Khaûo saùt söï bieán thieân vaø veõ ñoà thò (C) cuûa haøm soá ñaõ
cho.
2. Vieát phöông trình tieáp tuyeán cuûa (C), bieát tieáp tuyeán ñoù
vuoâng goùc vôùi tieäm caân xieân cuûa (C).
Caâu II: (2 ñieåm)
1. Giaûi phöông trình: cotgx + sinx(1 + tgx.tg x
2) = 4
2. Tìm m ñeå phöông trình sau coù 2 nghieäm thöïc phaân bieät:
2
xmx22x1++=+
Caâu III: (2 ñieåm)
Trong khoâng gian Oxyz, cho ñieåm A (0; 1; 2) vaø hai ñöôøng
thaúng d1 : x
y
1z1
21 1
−+
==
− vaø d2 :
x1t
y12
z2t
=+
⎧
⎪=− −
⎨
⎪=+
⎩
t
1. Vieát phöông trình maët phaúng (P) qua A, ñoàng thôøi song
song vôùi d1 vaø d2.
2. Tìm toïa ñoä caùc ñieåm M treân d1, N treân d2 sao cho 3
ñieåm A, M, N thaúng haøng.
Caâu IV: (2 ñieåm)
1. Tính I =
ln 5
xx
ln3
dx
e2e 3
−
+−
∫
2. Cho x, y laø caùc soá thöïc thay ñoåi. Tìm giaù trò nhoû nhaát
cuûa bieåu thöùc A = 22 22
(x 1) y (x 1) y y 2−++ +++−
Phaàn töï choïn : Thí sinh choïn caâu V.a hoaëc caâu V.b
CaâuV.a: Theo chöông trình THPT khoâng phaân ban (2 ñieåm)
1. Trong maët phaúng Oxy, cho ñöôøng troøn (C) : x2 + y2 – 2x
– 6y + 6 = 0 vaø ñieåm M (-3; 1). Goïi T1 vaø T2 laø caùc tieáp
ñieåm cuûa caùc tieáp tuyeán keû töø M ñeán (C). Vieát phöông
trình ñöôøng thaúng T1T2.
2. Cho taäp hôïp A goàm n phaàn töû (n ≥ 4). Bieát raèng soá taäp
con goàm 4 phaàn töû cuûa A baèng 20 laàn soá taäp con goàm 2
phaàn töû cuûa A. Tìm k ∈ ⎨1, 2, …, n⎬ sao cho soá taäp con
goàm k phaàn töû cuûa A laø lôùn nhaát.
Caâu V.b: Theo chöông trình THPT phaân ban thí ñieåm (2 ñieåm)
1. Giaûi baát phöông trình :
log
5(4x + 144) – 4log52 < 1 + log5(2x – 2 + 1)
2. Cho hình choùp S.ABCD coù ñaùy ABCD laø hình chöõ nhaät
vôùi AB = a, AD = a, SA = a vaø SA vuoâng goùc vôùi maët
phaúng (ABCD). Goïi M, N laàn löôït laø trung ñieåm cuûa AD vaø
SC; I laø giao ñieåm cuûa BM vaø AC. Chöùng minh raèng maët
phaúng (SAC) vuoâng goùc vôùi maët phaúng (SMB). Tính theå
tích cuûa khoái töù dieän ANIB.
2
BAØI GIAÛI
Caâu I:
1. y =
2
xx1
x2
+
−
+ = 1
x1x2
−+ +
D = R \ ⎨-2⎬
TCÑ : x = −2; TCX : y = x – 1
y' = 2
1
1=
(x 2)
−+
2
2
x4x3
(x 2)
+
+
+
y’ = 0 ⇔ x = −1 ∨ x = −3
x -∞ -3 -2 -1 +∞
y' + 0 − − 0 +
y -5
-∞ -∞
+∞ +∞
-1
Ñoà thò haøm soá :
2. Tieäm caän xieân coù heä soá goùc k1=1. Tieáp tuyeán vuoâng
goùc tieäm caän xieân ⇒heä soá goùc tieáp tuyeán laø k2 = −1.
⇒ Pt tieáp tuyeán coù daïng y = −x + m (D)
(D) tieáp xuùc (C) ⇔ Heä
2
1
11
(x 2)
1
x1 xm
x2
⎧−=−
⎪+
⎪
⎨
⎪−+ =−+
⎪+⎩
coù nghieäm
⇔
21
(x 2) 2
1
2(x 2) 5 m
x2
⎧+=
⎪
⎪
⎨
⎪
+
+−=
⎪+⎩
coù nghieäm
Vaäy : m = 22 5
−
∨ m = 22 5−−
Vaäy phöông trình 2 tieáp tuyeán laø y= −x – 5 22±
Caâu II.
1. Vôùi ñieàu kieän sin2x ≠ 0, ta coù:
x
1t
g
x.t
g
2
+ =
xx
cosx.cos sinx.sin 1
22
xcosx
cosx.cos 2
+
=
Vaäy phöông trình ñaõ cho ⇔ cosx sinx 4
sin x cos x
+=
(1)
⇔ sin2x = 1
2 ⇔ x = k
12
π+π
hay x = 5k
12
π
+
π
CÑ
CT
y
-2
-1
-3 -1
0 1
-5
-3
x

2. Caùch 1: Ycbt ⇔ x2 + mx + 2 = (2x + 1)2 coù 2 nghieäm
phaân bieät ≥ 1
2
−
⇔ f(x)=3x2+(4 – m)x – 1 = 0 coù 2 nghieäm phaân bieät ≥ 1
2
−
Vì a.c < 0 neân f(x) = luoân coù 2 nghieäm phaân bieät traùi daáu
Vaäy ycbt ⇔ f(x) = 0 coù ñuùng 1 nghieäm thoûa 1
2
− ≤ x < 0
Vì f(0) = −1 ≠ 0 neân ycbt ⇔ 1
f.f(0)
2
⎛⎞
−≤
⎜⎟
⎝⎠ 0
⇔ 1
f0
2
⎛⎞
−≥
⎜⎟
⎝⎠ ⇔ 1m
3. 2 1 0
42
−+ −≥ ⇔ 9
m2
≥
Caùch 2: 2
xmx22x++=+1
⇔
22
1
x2
x mx 2 4x 4x 1
⎧≥−
⎪
⎨
⎪++= ++
⎩
⇔
2
1
x2
3x 4x 1 mx
⎧≥−
⎪
⎨
⎪+−=
⎩
⇔
1
x2
1
3x 4 m (do x=0 khoân
g
laø n
g
hieäm)
x
⎧≥−
⎪
⎪
⎨
⎪+− =
⎪
⎩
Xeùt y = 3x + 4 1
x
− (C’) vôùi x ≥ −1
2 vaø x ≠ 0
Ta coù : y’ = 3 + 2
1
x > 0 ∀ x ≠ 0
x 12
− 0 +∞
y' + +
y +∞
9
2
+∞
-∞
Ycbt ⇔ (d) y = m caét (C’) taïi 2 ñieåm phaân bieät ⇔ 9m
2
≤
Caâu III
1. Maët phaúng (P) coù 1 caëp VTCP :
1
a
uur
=(2, 1, -1) vaø 2
a
uur
=(1, -2, 1)
⇒ (P) coù 1 PVT laø (1; 3; 5)
Vaäy ptrình mp (P) laø: 1(x – 0) + 3(y – 1) + 5(z – 2) = 0
Hay x + 3y + 5z – 13 = 0
2. Goïi M (2t’, 1+t’, −1–t’) ∈ d1; N (1+t, −1–2t, 2+t) ∈ d2
Vaäy AM (2t',t', 3 t')=−−
uuuur
; AN (1 t, 2 2t,t)=+−−
uuur
A, M, N thaúng haøng ⇔ AM
uuuur
cuøng phöông vôùi AN
uuur
⇔ 2t' t' 3 t'
1t 22t t
−−
==
+−− ⇔
4t'(1 t) t'(1 t) 0
2tt' (1 t)(3 t') 0
++ +=
⎧
⎨++ + =
⎩
⇔ ⇔
t' 0 (1 t) 0
2tt' (1 t)(3 t') 0
=∨ + =
⎧
⎨++ + =
⎩
t' 0
t1
=
⎧
⎨=−
⎩
Do ñoù M (0, 1, −1) vaø N (0, 1, 1)
Caâu IV.
1. I =
ln5 x
2x x
ln3
edx
e3e−+
2
∫
Ñaët t = ex ⇒ dt = exdx vaø t (ln3) = 3; t(ln5) = 5
I =
55
2
33
dt dt
t3t2 (t1)(t2
=)
−
+−−
∫∫=
5
3
11
dt
t2 t1
⎛⎞
−
⎜⎟
−−
⎝⎠
∫
=
5
3
t2
ln t1
⎡
⎤
−
⎢
⎥
−⎦ = 3
ln 2
⎣
2. Caùch 1 : Xeùt a (1 x,
y
)=−
r
; b (1 x,
y
)=+
r
A =
ab
y
2ab
y
221 2
yy
2
+
+−≥++−= + +−
rr rr
Daáu “=” xaûy ra khi x = 0
Aùp duïng BÑT BCS 22
3
y
1
y
421
y
+≤ + = +
⇒ A ≥
y
32
yy
32
y
23++−≥++−=+
daáu “=” xaûy ra khi y = 1
3
⇒ A ≥ 23+ daáu “=” khi x = 0, y = 1
3
Vaäy : min A = 2 + 3 khi x = 0, y = 1
3
Caùch 2: Xeùt a (1 x,
y
)=−
r
; b (1 x,
y
)=+
r
A = 2
ab
y
2ab
y
221
yy
2
+
+−≥++−= + +−
rr rr
Daáu “=” xaûy ra khi x = 0
Xeùt g(y) = 2
21
yy
2+−
+
• y ≥ 2 : g(y) = 2
21
yy
2+− : luoân taêng
+
• y < 2 : g(y) = 2
21
y
2
y
++−
g’(y) = 2
2
y
1
1y
−
+, g’(y) = 0 ⇔ y = 1
3
Laäp baûng bieán thieân ta coù:
g(y)
23≥+ , daáu “=” khi y = 1
3
Vaäy : min A = 2 + 3 khi x = 0, y = 1
3
Caùch 3:
Aùp duïng BÑT BCS :
22 22
3131
(1 ) (1 ) ( 1)
2244
−
+≤+ −+= −+
x
yxyxy
22 22
3131
(1 ) (1 ) ( 1)
2244
+
+≤+ ++= ++
x
yxyxy
Vaäy A 3131
(1 ) (1 ) 2
2222
≥−
+++++−xy xyy
331 331
22
22 2 22 2 3+++ ++−=+xy xy y≥−
daáu “=” xaûy ra khi x = 0, y = 1
3
Caâu V.a.
1. (C) coù taâm I (1; 3), R = 2
Ñöôøng troøn ñöôøng kính MI coù taâm J (−1, 2)
R’ = MJ = 41 5+=
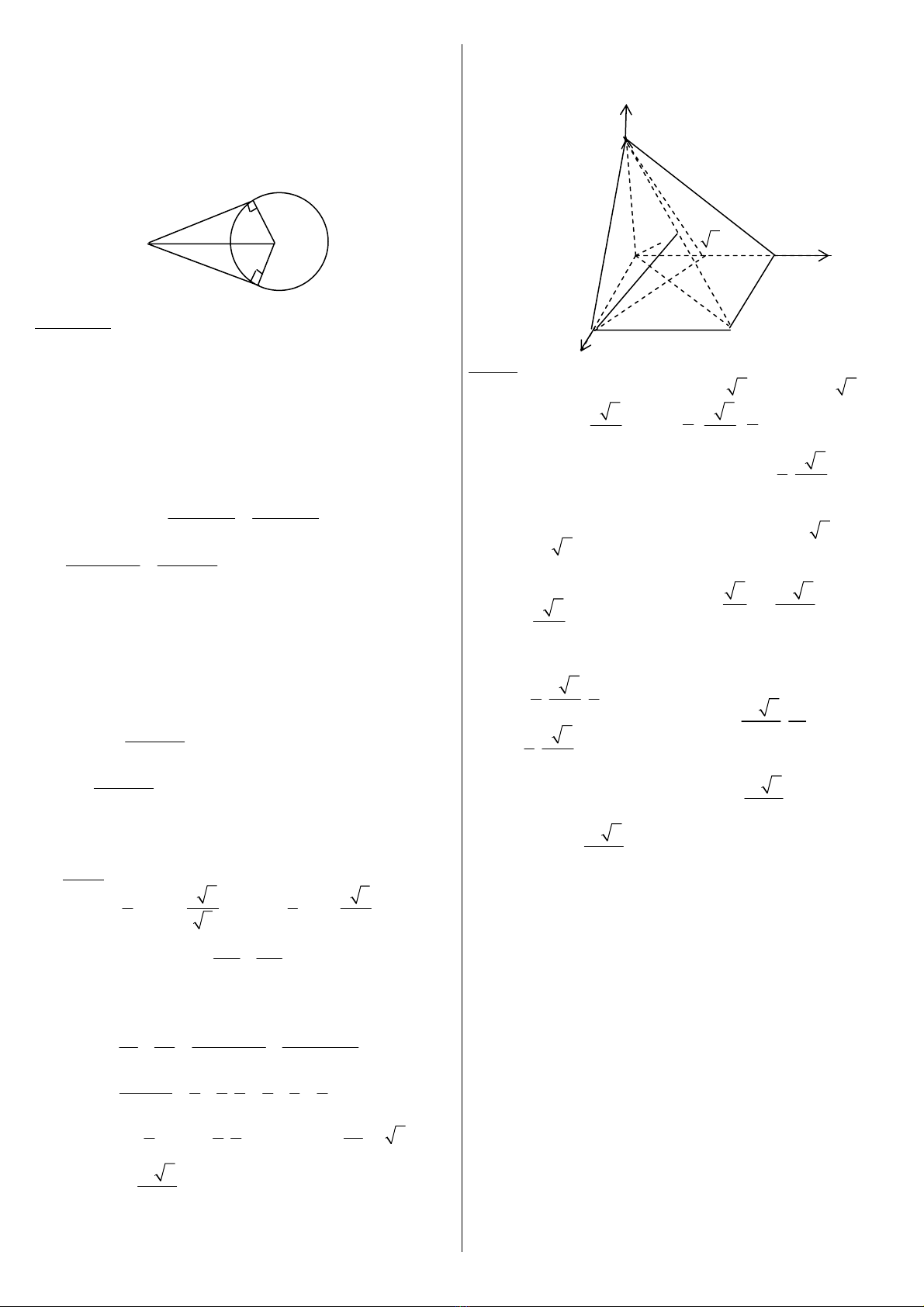
Phöông trình ñöôøng troøn (C’) ñöôøng kính MI laø:
(x + 1)
2 + (y – 2)2 = 5
⇔ x2 + y2 + 2x – 4y = 0 (C’)
T
1T2 chính laø truïc ñaúng phöông (C) vaø (C’)
Phöông trình T1T2 :
x
2 + y2 – 2x – 6y + 6 = x2 + y2 + 2x – 4y
⇔ 2x + y – 3 = 0
Caùch khaùc : Goïi T (x0, y0) laø tieáp ñieåm cuûa tieáp tuyeán Δ
vôùi (C). Pt Δ laø: x0x + y0y – (x + x0) – 3(y + y0) + 6 = 0
M (−3, 1) ∈ Δ ⇔ −3x0 + y0 – x0 + 3 – 3y0 – 3 + 6 = 0
⇔ 2x0 + y0 – 3 = 0
Vì T1, T2 laø tieáp ñieåm ⇒
⎧
⎨11
22
23
23
+−=0
0+−=
⎩
x
y
xy
Vaäy Pt T1T2 : 2x + y – 3 = 0
2. ⇔
42
nn
C20C=n! 20n!
4!(n 4)! 2!(n 2)!
=
−−
12
24.(n 4)! 2(n 2)!
=
−−
0
1
1
≥
⎪
⎩
⇔ (n – 3)(n – 2) = 20.12
⇔ n = 18 (vì n ≥ 4)
Ycbt ⇒ ⎪
⎨ ⇒ k = 9
kk
18 18
kk
18 18
CC
CC
−
+
⎧≥
Caâu V.b.
1. Baát phöông trình ñaõ cho töông ñöông :
x
x2
55
4 144
lo
g
lo
g
5(2 1)
16
−
+<+
⇔
x
x2
4144
5(2 1)
16
−
+<+
⇔
xx
414480(2 1
−
+< +
2
)
⇔ ⇔
x
42 16<< 2x4
<
<
2. Caùch 1: Deã thaáy I laø troïng taâm ΔABD
⇒ BI = 2BM
3 = a2
3 vaø AI = 1a
AC
33
=3
ΔABI coù BI2 + AI2 =
22
22
2a 3a aAB
39
+==
⇒ BI⊥ AI vaø BI ⊥ SA ⇒ BI⊥(SAC) ⇒(SMB) ⊥ (SAC)
Goïi V = VSABC; V1 = VSABN; V2 = VCNBI
Ta coù : 12
VVSN.SA.SB CN.CI.CB
V V SC.SA.SB SC.CA.CB
+= +
12
VV 112115
.
V22323
+=+ =+=
6
⇒ VANIB = SABC
111
V.BA.BC.
S
666
=A
= 1a.a 2.a
36
⇒ VANIB =
3
a2
36
Caùch 2: Choïn heä truïc nhö hình veõ.
z
x
B
S
D
AN
M
I
a
a
M I
T1
T2
•
J a2
C
y
Ta coù A (0, 0, 0); B (a, 0, 0); C (a, a2
, 0); D (0, a, 0);
S (0, 0, a); M (0,
2
a2
2, 0); N ( a
2,a2
2,a
2)
• I laø troïng taâm ΔABD ⇒ IC 2IA=−
uuruur
⇒ I aa2
;;0
33
⎛⎞
⎜⎟
⎜⎟
⎝⎠
• AS (0,0,a)
AC (a,a 2,0)
⎫
=
⎪
⎬
=
⎪
⎭
uuur
uuur ⇒ (SAC)
nAS,A
⎡⎤
=⎣⎦
C
ruuur uuur
= 22
(a 2,a,0)−
SB (a,0, a)
a2
SM (0, , a)
2
⎫
=−
⎪
⎬
=−
⎪
⎭
uur
uuur ⇒
2
22
(SMB) 2a2
na
;a;
22
⎛⎞
=⎜⎟
⎜⎟
⎝⎠
r
0
Ta coù : 44
(SAC) (SMB)
n.n aa
=
−=
rr
⇒ (SAC) ⊥ (SMB)
• aa2a
AN ( ; ; )
222
aa2
AI ( ; ;0)
33
⎫
=
⎪
⎪
⎬
⎪
=
⎪
⎭
uuur
uur
⇒
22
a2a
AN.AI ( , ,0)
66
⎡⎤
=−
⎣⎦
uuur uur
AB
uuur
= (a, 0, 0) ⇒
3
a2
AN.AI .AB 6
⎡⎤
=−
⎣⎦
uuur uur uuur
⇒ VANIB =
3
a2
36
HAØ VAÊN CHÖÔNG, PHAÏM HOÀNG DANH,
HOÀ VÓNH ÑOÂNG, TRAÀN VAÊN TOAØN,
LEÂ NGOÂ THIEÄN, TRAÀN MINH THÒNH, NGUYEÃN PHUÙ VINH
(Trung taâm Boài döôõng vaên hoùa &
Luyeän thi ñaïi hoïc Vónh Vieãn)
















