Đáp án - Thang điểm Kỳ thi tuyển sinh đại học, cao đẳng năm 2004 môn Toán, khối A (Đáp án chính thức) - Bộ GD&ĐT

Chia sẻ: đinh Công Chánh | Ngày: | Loại File: PDF | Số trang:4

Thêm vào BST

Báo xấu

96
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Cùng tham khảo Đáp án - Thang điểm Kỳ thi tuyển sinh đại học, cao đẳng năm 2004 môn Toán, khối A (Đáp án chính thức) của Bộ GD&ĐT để biết được kết quả làm bài của mình sau khi thử sức mình với đề thi tuyển sinh đại học, cao đẳng năm 2004 môn Toán, khối A (Đề thi chính thức) của Bộ GD&ĐT. Chúc các bạn ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh CĐ-ĐH.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đáp án - Thang điểm Kỳ thi tuyển sinh đại học, cao đẳng năm 2004 môn Toán, khối A (Đáp án chính thức) - Bộ GD&ĐT

Bé gi¸o dôc vµ ®µo t¹o §¸p ¸n - Thang ®iÓm ..................... ®Ò thi tuyÓn sinh ®¹i häc, cao ®¼ng n¨m 2004 ........................................... §Ò chÝnh thøc M«n: To¸n, Khèi A (§¸p ¸n - thang ®iÓm cã 4 trang) C©u ý Néi dung §iÓm I 2,0 I.1 (1,0 ®iÓm) − x 2 + 3x − 3 1 1 y= = − x +1− . 2(x − 1) 2 2 ( x − 1) a) TËp x¸c ®Þnh: R \ {1} . b) Sù biÕn thiªn: x(2 − x) y' = ; y ' = 0 ⇔ x = 0, x = 2 . 0,25 2(x − 1) 2 1 3 yC§ = y(2) = − , yCT = y(0) = . 2 2 §−êng th¼ng x = 1 lµ tiÖm cËn ®øng. 1 §−êng th¼ng y = − x + 1 lµ tiÖm cËn xiªn. 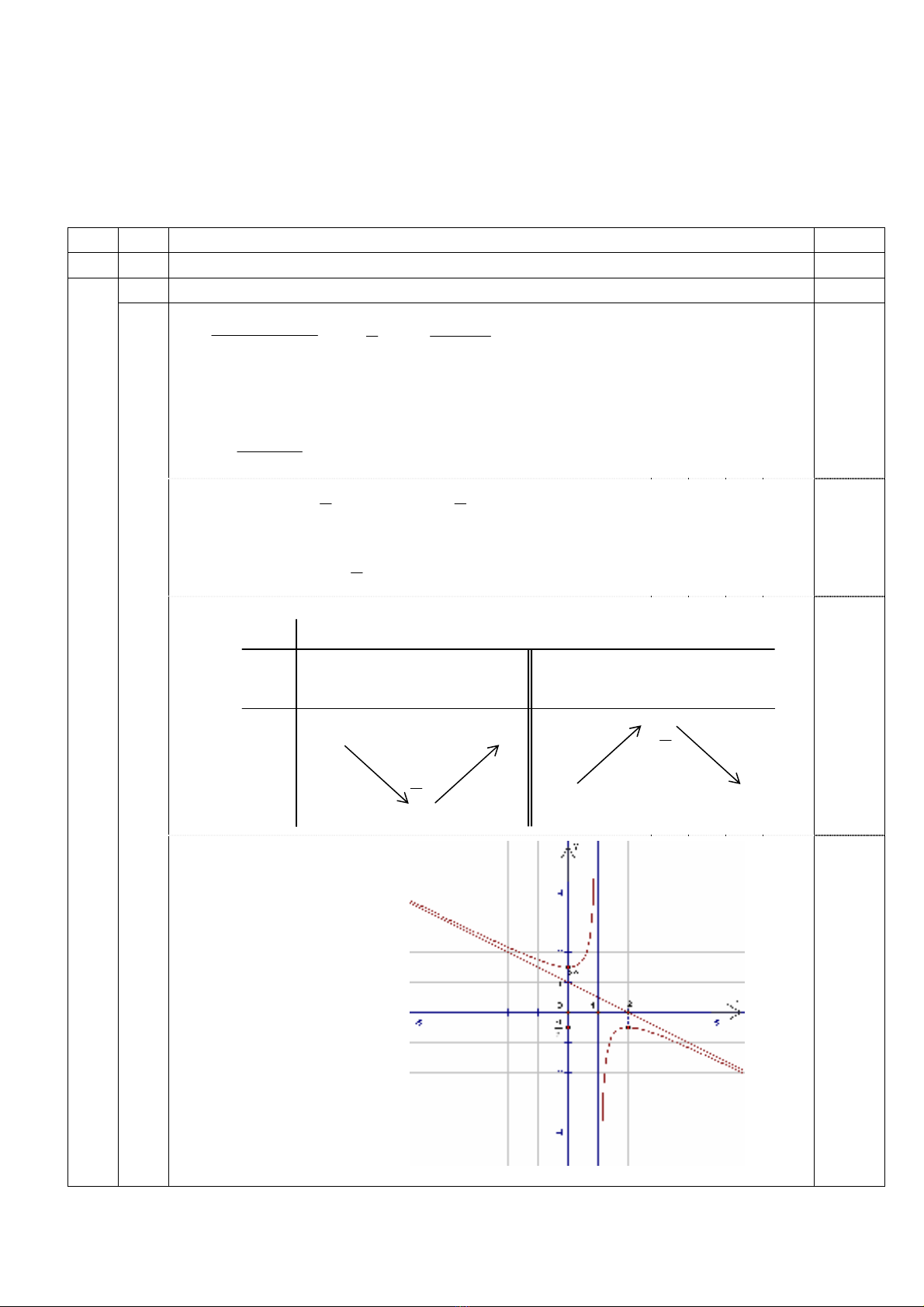0,25 2 B¶ng biÕn thiªn: x −∞ 0 1 2 +∞ y' − 0 + + 0 − 1 y +∞ +∞ − 2 3 0,25 −∞ −∞ 2 c) §å thÞ: 0,25 1
I.2 (1,0 ®iÓm) Ph−¬ng tr×nh hoµnh ®é giao ®iÓm cña ®å thÞ hµm sè víi ®−êng th¼ng y = m lµ : − x 2 + 3x − 3 = m ⇔ x 2 + (2 m − 3)x + 3 − 2 m = 0 (*). 0,25 2(x − 1) Ph−¬ng tr×nh (*) cã hai nghiÖm ph©n biÖt khi vµ chØ khi: 3 1 ∆ > 0 ⇔ 4m 2 − 4m − 3 > 0 ⇔ m > hoÆc m < − (**) . 0,25 2 2 Víi ®iÒu kiÖn (**), ®−êng th¼ng y = m c¾t ®å thÞ hµm sè t¹i hai ®iÓm A, B cã hoµnh ®é x1 , x2 lµ nghiÖm cña ph−¬ng tr×nh (*). (x + x 2 ) − 4x1x 2 = 1 2 2 AB = 1 ⇔ x 1 − x 2 = 1 ⇔ x1 − x 2 =1 ⇔ 1 0,25 1± 5 ⇔ (2 m − 3)2 − 4(3 − 2 m ) = 1 ⇔ m= (tho¶ m·n (**)) 0,25 2 II 2,0 II.1 (1,0 ®iÓm) §iÒu kiÖn : x ≥ 4 . 0,25 BÊt ph−¬ng tr×nh ®· cho t−¬ng ®−¬ng víi bÊt ph−¬ng tr×nh: 2(x 2 − 16) + x − 3 > 7 − x ⇔ 2(x 2 − 16) > 10 − 2x 0,25 + NÕu x > 5 th× bÊt ph−¬ng tr×nh ®−îc tho¶ m·n, v× vÕ tr¸i d−¬ng, vÕ ph¶i ©m. 0,25 + NÕu 4 ≤ x ≤ 5 th× hai vÕ cña bÊt ph−¬ng tr×nh kh«ng ©m. B×nh ph−¬ng hai vÕ ta ( ) ®−îc: 2 x 2 − 16 > (10 − 2x ) ⇔ x 2 − 20x + 66 < 0 ⇔ 10 − 34 < x < 10 + 34 . 2 KÕt hîp víi ®iÒu kiÖn 4 ≤ x ≤ 5 ta cã: 10 − 34 < x ≤ 5 . §¸p sè: x > 10 − 34 0,25 II.2 (1,0 ®iÓm) §iÒu kiÖn: y > x vµ y > 0. 1 log 1 (y − x ) − log 4 1 =1 ⇔ − log 4 (y − x ) − log 4 =1 0,25 y y 4 y−x 3y ⇔ − log 4 =1 ⇔ x = . 0,25 y 4 2 ⎛ 3y ⎞ 2 ThÕ vµo ph−¬ng tr×nh x + y = 25 ta cã: ⎜ ⎟ + y = 25 ⇔ y = ±4. 2 2 0,25 ⎝ 4 ⎠ So s¸nh víi ®iÒu kiÖn , ta ®−îc y = 4, suy ra x= 3 (tháa m·n y > x). VËy nghiÖm cña hÖ ph−¬ng tr×nh lµ (3; 4). 0,25 III 3,0 III.1 (1,0 ®iÓm) JJJG + §−êng th¼ng qua O, vu«ng gãc víi BA( 3 ; 3) cã ph−¬ng tr×nh 3x + 3y = 0 . JJJG §−êng th¼ng qua B, vu«ng gãc víi OA(0; 2) cã ph−¬ng tr×nh y = −1 0,25 JJJG ( §−êng th¼ng qua A, vu«ng gãc víi BO( 3 ; 1) cã ph−¬ng tr×nh 3x + y − 2 = 0 ) Gi¶i hÖ hai (trong ba) ph−¬ng tr×nh trªn ta ®−îc trùc t©m H( 3 ; − 1) 0,25 + §−êng trung trùc c¹nh OA cã ph−¬ng tr×nh y = 1. §−êng trung trùc c¹nh OB cã ph−¬ng tr×nh 3x + y + 2 = 0 . 0,25 ( §−êng trung trùc c¹nh AB cã ph−¬ng tr×nh 3x + 3y = 0 ). 2
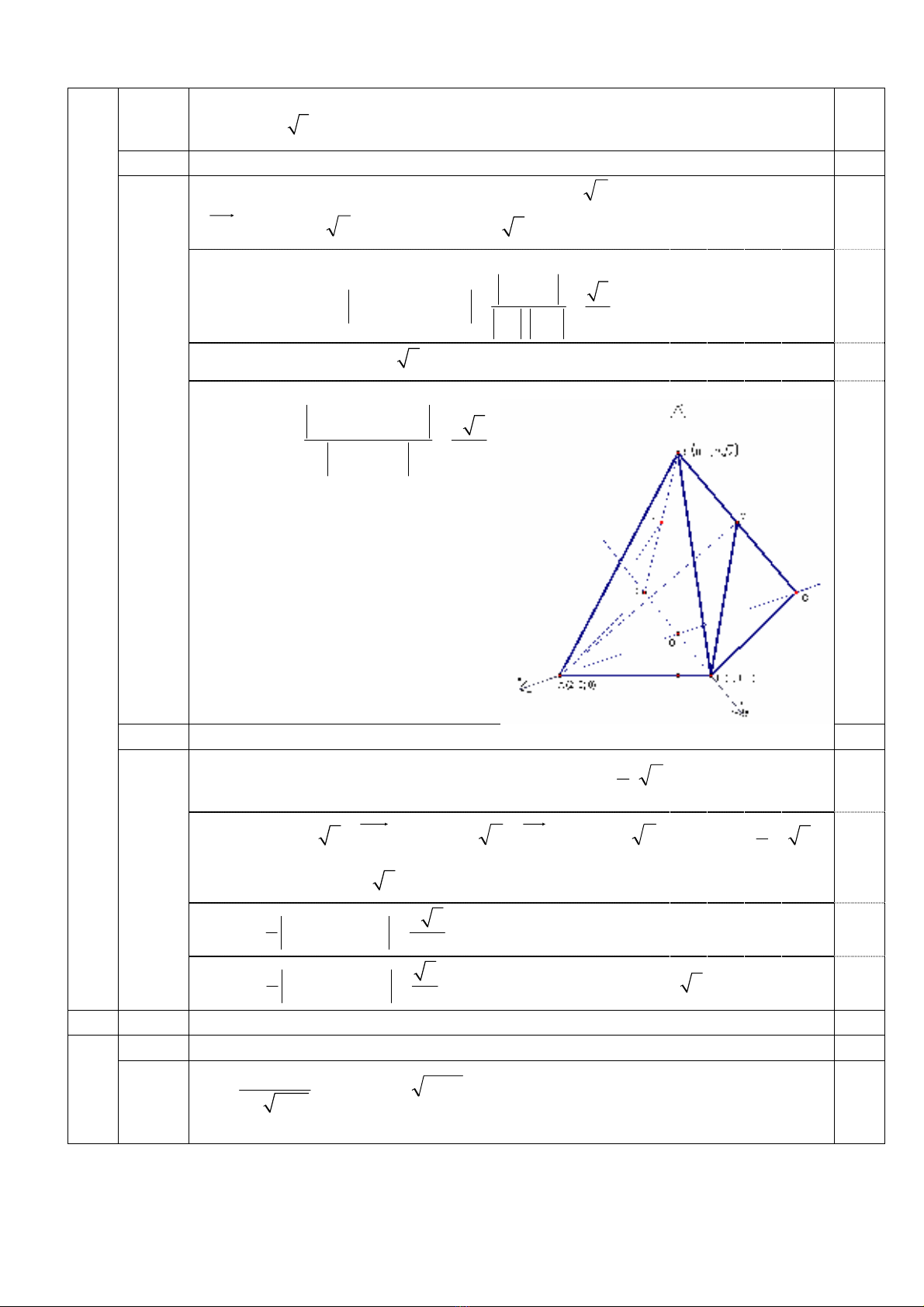
Gi¶i hÖ hai (trong ba) ph−¬ng tr×nh trªn ta ®−îc t©m ®−êng trßn ngo¹i tiÕp tam gi¸c ( OAB lµ I − 3 ; 1 . ) 0,25 III.2.a (1,0 ®iÓm) + Ta cã: C ( −2; 0; 0 ) , D ( 0; −1; 0 ) , M − 1; 0; 2 , ( ) ( JJJJG ) SA = 2; 0; − 2 2 , BM = −1; −1; 2 . ( ) 0,25 Gäi α lµ gãc gi÷a SA vµ BM. JJJG JJJJG JJJG JJJJG SA.BM 3 Ta ®−îc: cosα = cos SA, BM ( ) = JJJG JJJJG = SA . BM 2 ⇒ α = 30° . 0,25 JJJG JJJJG JJJG ( + Ta cã: ⎡⎣SA, BM ⎤⎦ = −2 2; 0; − 2 , AB = ( −2; 1; 0 ) .) 0,25 VËy: JJJG JJJJG JJJG ⎡SA, BM ⎤ ⋅ AB ⎣ ⎦ 2 6 d ( SA, BM ) = JJJG JJJJG = 0,25 ⎡SA, BM ⎤ 3 ⎣ ⎦ III.2.b (1,0 ®iÓm) ⎛ 1 ⎞ Ta cã MN // AB // CD ⇒ N lµ trung ®iÓm SD ⇒ N⎜ 0; − ; 2 ⎟ . ⎝ 2 ⎠ 0,25 JJJG ( ) ( ) JJJG ⎛ 1 ( ⎞ SA = 2; 0; −2 2 , SM = − 1; 0; − 2 , SB = 0; 1; − 2 2 , SN = ⎜ 0; − ; − 2 ⎟ ⎝ 2 ⎠ ) JJJG JJJG ( ⇒ ⎡⎣SA, SM ⎤⎦ = 0; 4 2; 0 . ) 0,25 1 JJJG JJJG JJG 2 2 VS.ABM = ⎡⎣SA,SM ⎤⎦ ⋅ SB = 0,25 6 3 1 ⎡ JJJG JJJG ⎤ JJJG 2 VS.AMN = SA,SM ⋅ SN = ⇒ VS.ABMN = VS.ABM + VS.AMN = 2 6⎣ ⎦ 0,25 3 IV 2,0 IV.1 (1,0 ®iÓm) 2 x I= 1 ∫ 1+ x −1 dx . §Æt: t = x − 1 ⇒ x = t 2 + 1 ⇒ dx = 2 tdt . x = 1⇒ t = 0 , x = 2 ⇒ t = 1. 0,25 3
1 1 1 t2 +1 t3 + t ⎛ 2 ⎞ Ta cã: I = ∫ 2t dt = 2∫ dt = 2∫ ⎜ t 2 − t + 2 − ⎟ dt 0 1+ t 0 1 + t 0 ⎝ t + 1 ⎠ 0,25 1 ⎡1 1 ⎤ I = 2 ⎢ t 3 − t 2 + 2t − 2 ln t + 1 ⎥ 0,25 ⎣3 2 ⎦0 ⎡1 1 ⎤ 11 I = 2 ⎢ − + 2 − 2 ln 2 ⎥ = − 4 ln 2 . 0,25 ⎣3 2 ⎦ 3 IV.2 (1, 0 ®iÓm) 8 ⎡⎣1 + x 2 (1 − x ) ⎤⎦ = C80 + C18 x 2 (1 − x ) + C82 x 4 (1 − x ) + C83 x 6 (1 − x ) + C84 x 8 (1 − x ) 2 3 4 + C85 x10 (1 − x ) + C86 x12 (1 − x ) + C87 x14 (1 − x ) + C88 x16 (1 − x ) 5 6 7 8 0,25 BËc cña x trong 3 sè h¹ng ®Çu nhá h¬n 8, bËc cña x trong 4 sè h¹ng cuèi lín h¬n 8. 0,25 VËy x8 chØ cã trong c¸c sè h¹ng thø t−, thø n¨m, víi hÖ sè t−¬ng øng lµ: C83.C32 , C84 .C 04 0,25 Suy ra a8 = 168 + 70 = 238 . 0,25 V 1,0 Gäi M = cos 2 A + 2 2 cos B + 2 2 cos C − 3 B+C B−C = 2 cos 2 A − 1 + 2 2 ⋅ 2 cos ⋅ cos −3. 0,25 2 2 A B−C A Do sin > 0 , cos ≤ 1 nªn M ≤ 2 cos 2 A + 4 2 sin − 4 . 0,25 2 2 2 2 MÆt kh¸c tam gi¸c ABC kh«ng tï nªn cos A ≥ 0 , cos A ≤ cos A . Suy ra: A ⎛ A⎞ A M ≤ 2 cos A + 4 2 sin − 4 = 2⎜ 1 − 2 sin 2 ⎟ + 4 2 sin − 4 2 ⎝ 2⎠ 2 2 A 2 A ⎛ A ⎞ 0,25 = −4 sin + 4 2 sin − 2 = −2⎜ 2 sin − 1 ⎟ ≤ 0 . VËy M ≤ 0 . 2 2 ⎝ 2 ⎠ ⎧ ⎪cos 2 A = cos A ⎪ ⎪ B−C ⎧A = 90° Theo gi¶ thiÕt: M = 0 ⇔ ⎨cos =1 ⇔⎨ ⎪ 2 ⎩B = C = 45°⋅ ⎪ A 1 ⎪sin 2 = 0,25 ⎩ 2 4