Đ THI TH Đ I H C S 195Ề Ử Ạ Ọ Ố
PH N CHUNGẦ:( 7 đi m) ể
Câu I: (2,0 đi mể) Cho hàm s y = ố
2
(2 1) (1)
1
m m x
x
− + −
−
(m là tham s )ố
1. Kh o sát s bi n thiên và v đ th c a hàm s (1) ng v i m = 0. ả ự ế ẽ ồ ị ủ ố ứ ớ
2. Ch ng minh r ng v i m i giá tr ứ ằ ớ ọ ị m khác 1, đ th c a hàm s (1) luôn ti p xúc v i đ ng th ng y =ồ ị ủ ố ế ớ ườ ẳ
x.
Câu II. (2,0 đi mể) 1. Gi i ph ng trìnhả ươ :
)
2
sin(2
cossin
2sin
cot
2
1
π
+=
+
+x
xx
x
x
2. Gi i h ph ng trình: ả ệ ươ
+ = − +
+ − + = + + − +
2 2
2 2 2 2 3 3 2
3 4 1
3 ( 9) 2 ( 9) 18( ) 2 (7 ) 3
x y x y
x x y y x y y y
.
Câu III. (1,0 đi mể) Tính tích phân :
∫
+
+
=
e
dxxx
xx
x
I
1
2ln3
ln1
ln
.
Câu IV. (1,0 đi mể) Cho hình chóp S.ABCD có đáy ABCD là hình vuông c nh ạ
a
, tam giác SAB đ u, tam giácề
SCD vuông cân t i S. G i I, J, K l n l t là trung đi m c a các c nh AB, CD, SA. Ch ng minh r ngạ ọ ầ ượ ể ủ ạ ứ ằ
( ) ( )SIJ ABCD⊥
. Tính th tích kh i chóp K.IBCD.ể ố
Câu V. (1,0 đi mể) Cho x, y thay đ i tho mãn: ổ ả
2 2
2 3 1x y+ >
và
. Tìm
giá tr l n nh t c a bi u th c: ị ớ ấ ủ ể ứ
= +3 2P x y
.
PH N RIÊNGẦ:( 3 đi m) Thí sinh ch đ c làm m t trong hai ph n( ph n A ho c ph n B)ể ỉ ượ ộ ầ ầ ặ ầ
Ph n A: Theo ch ng trình chu nầ ươ ẩ
Câu VI a. ( 2 đi m) ể
1. Trong m t ph ng v i h t a đ Oxy, hãy tính di n tích c a tam giác đ u ABC n i ti p elip (E) có ph ngặ ẳ ớ ệ ọ ộ ệ ủ ề ộ ế ươ
trình
2 2
1
16 4
x y
+ =
nh n đi m A( 0;2) làm đ nh và tr c tung làm tr c đ i x ng?ậ ể ỉ ụ ụ ố ứ
2. Trong không gian v i h t a đ Oxyz, cho đi m A( 10;2;-1) và đ ng th ng d có ph ng trìnhớ ệ ọ ộ ể ườ ẳ ươ
1 1
2 1 3
x y z− −
= =
. L p ph ng trình mp(P) đi qua đi m A , song song d và kho ng cách t đ ng th ng dậ ươ ể ả ừ ườ ẳ
đ n mp(P) là l n nh t?ế ớ ấ
Câu VII a. (1 đi m) ểCh ng minh r ng : ứ ằ
0 2 4 6 98 100 50
100 100 100 100 100 100
...... 2C C C C C C− + − + − + = −
Ph n B: Theo ch ng trình nâng caoầ ươ
Câu VI b. ( 2 đi m) ể
1. Trong m t ph ng v i h t a đ Oxy, cho tam giác ABC có A (1;3), B( -1;1) , C( 3;0). L p ph ng trìnhặ ẳ ớ ệ ọ ộ ậ ươ
đ ng th ng ườ ẳ
V
? Bi t ế
V
qua A và cùng v i đ ng th ng d cũng qua A chia tam giác ABC thành 3 ph n cóớ ườ ẳ ầ
di n tích b ng nhau?ệ ằ
2. Trong không gian Oxyz cho m t c u (S) có ph ng trình ặ ầ ươ
2 2 2 2 2 2 0x y z x z+ + − + − =
. Tìm đi m Aể
thu c m t c u (S) sao cho kho ng cách t đi m A đ n m t ph ng (P) có ph ng trình ộ ặ ầ ả ừ ể ế ặ ẳ ươ
2 2 6 0x y z− + + =
l n nh t?ớ ấ
Câu VII b. ( 1 đi m)ể
Ch ng minh s ph c z v i z = ứ ố ứ ớ
2 3 20
1 (1 3) (1 3) (1 3) ... (1 3)i i i i+ + + + + + + + +
là s thu n o?ố ầ ả
1
CÂU N I DUNGỘĐI MỂ
I-1
(1 đ)
y =
2
(2 1) (1)
1
m m x
x
− + −
−
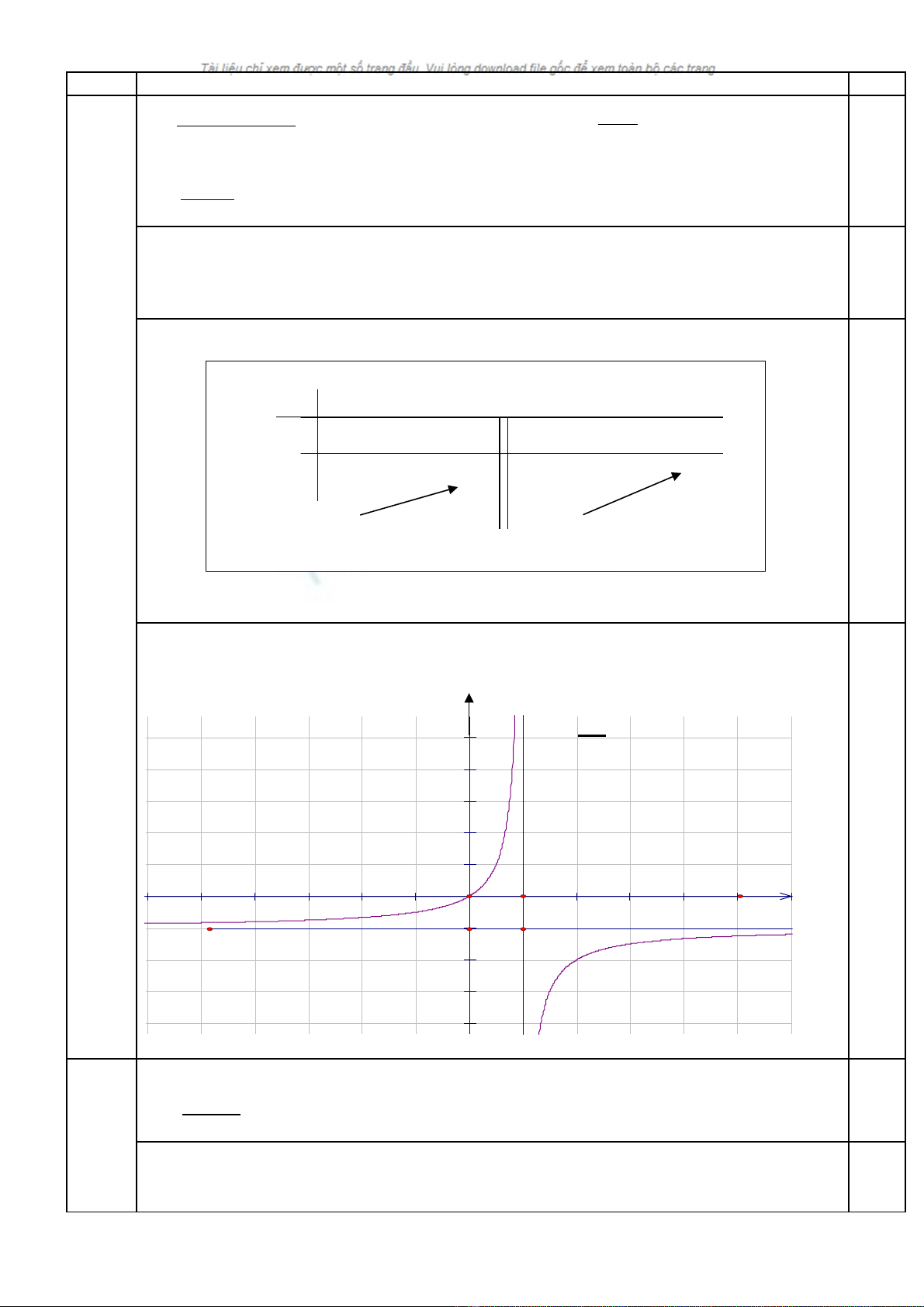
. Khi m = 0 : Ta có hàm s y = ố
1
x
x
−
−
TXĐ : D = R\{1}
y’ =
2
10, 1
( 1) x
x> ∀
−
0,25
lim ( ) lim ( ) 1
x x
f x f x
+ −
= = −
, nên y = -1 là ti m c n ngang c a đ th hàm sệ ậ ủ ồ ị ố
1 1
lim ( ) , lim
x x
f x
+ −
= − = +
, nên x = 1 là ti m c n đ ng c a đ th hàm sệ ậ ứ ủ ồ ị ố
0,25
B ng bi n thiênả ế :
Hàm s đ ng bi n trên các kho ng ố ồ ế ả
( ;1)−
và
(1; )+
Hàm s không có c c trố ự ị
0,25
Đ thồ ị :
Nh n xétậ : Đ th nh n giao đi m c a 2 đ ng ti m c n I(1ồ ị ậ ể ủ ườ ệ ậ ;-1) làm tâm đ i x ngố ứ
y
4
2
-2
-4
-1
-5
5
y=f(x)
y=-1
x=1
f
x
()
=
-x
x-1
I
O
1
0,25
I
2
(1 đ)
V i ớ
1x
, ta có:
2
2
( 1)
'( 1)
m
yx
−
=−
0,25
Xét h đi u ki n ti p xúc c a đ th hàm s (1) v i đ ng th ng y = xệ ề ệ ế ủ ồ ị ố ớ ườ ẳ
2
x1
−
f’(x
)
f(x)
(
+
−
1
−
1
−
+
+
là :
2
2
2
(2 1)
1(*)
( 1) 1;( 1)
( 1)
m m x x
x
mx
m
− + −
=
−
−
=
−
Yêu c u bài toán, ta s ch ng minh h (*) có nghi m v i m i ầ ẽ ứ ệ ệ ớ ọ
1m
.
0,25
Th t v y (*)ậ ậ
2
2
2
1
( ) 0
( 1) 1
( 1)
x
x m
m
x
− =�−
=
−
2
2
1
( 1) 1
( 1)
x
m x
m
x
=�−
=
−
.Luôn đúng v i m i m khác 1 (■)ớ ọ
0,5
II-1
(1 đ)
Đi u ki n: ề ệ
.0cossin,0sin ≠+≠ xxx
0,25
PT ⇔
0cos2
cossin
cossin2
sin2
cos =−
+
+x
xx
xx
x
x
2
cos 2cos 0
sin cos
2 sin
x x
x x
x− =�+
cos sin( ) sin2 0
4
x x x
π
� �
+ − =�� �
� �
0,25
+)
.,
2
0cos ∈+=⇔= kkxx
π
π
+)
∈
+=
+=
⇔
+−−=
++=
⇔+= nm
n
x
mx
nxx
mxx
xx ,
3
2
4
2
4
2
4
2
2
4
2
)
4
sin(2sin
ππ
π
π
π
π
π
π
π
π
.,
3
2
4
∈+=⇔ t
t
x
ππ
0,25
Đ i chi u đi u ki n ta có nghi m c a pt là ố ế ề ệ ệ ủ
π
π
kx += 2
;
.,,
3
2
4
∈+= tk
t
x
ππ
0,25
II-2
(1 đ) Bi n đ i h v d ng:ế ổ ệ ề ạ
2 2
2 2 2 2
( 3 ) ( 4 ) 1
3( 3 ) 2( 4 ) 3
x x y y
x x y y
− + + =
− − + =
Đ t ặ
= −
= +
2
2
3
4
u x x
v y y
ta có h ph ng trình: ệ ươ
+ =
− =
2 2
1
3 2 3
u v
u v
0,25
3