Đ KI M TRA 1 TI T (Bài s 2 )Ề Ể Ế ố
L p 11 ớ– Năm h c: 2013- 2014ọ
Môn: Hình h c Th i gian: 45 phútọ ờ
Câu 1. Trong mp Oxy, cho đi m ể
( )
2; 7A−
và đng tròn (C): ườ
( )
22
3 100x y+ + =
a) Tìm nh c a đi m A qua phép t nh ti n theo véc t ả ủ ể ị ế ơ
( 2;1)v−
r
b) Vi t ph ng trình đng tròn nh c a (C ) qua phép t nh ti n theo véc t ế ươ ườ ả ủ ị ế ơ
( 2;1)v−
r
.
Câu 2 . Vi t ph ng trình nh c a đng th ng ế ươ ả ủ ườ ẳ
:3 2 12 0d x y− − =
qua phép quay tâm
O góc
0
90
.
Câu 3.
a) Tìm nh c a tam giác ABC có ba góc nh n qua phép v t tâm H là tr c tâm c a tam ả ủ ọ ị ự ư ủ
giác ABC có t s v t ỉ ố ị ự
1
2
k=
b) Cho hình ch nh t ABCD tâm I. G i J, K,L l n l t là trung đi m c a BC,CJ và CI. ữ ậ ọ ầ ượ ể ủ
Ch ng minh hai hình thang IJKL và DCJI đng d ng.ứ ồ ạ
Câu 4.
a) Vi t ph ng trình (C’) là nh c a đng tròn(C): ế ươ ả ủ ườ
2 2 2 4 4 0x y x y+ + − − =
qua phép vị
t tâm O, t s k=2. Tìm t a đ tâm v t ngoài K c a hai đng tròn (C) và (C’)ự ỉ ố ọ ộ ị ự ủ ườ
b) Cho đi m A n m ngoài đng tròn (O;R) và hai đi m B,C thay đi trên (O) sao cho ể ằ ườ ể ổ
đ dài đo n th ng BC luôn b ng ộ ạ ẳ ằ
3R
. Tìm qu tích tr ng tâm G c a tam giác ABC.ỹ ọ ủ
………………………………………
Đ KI M TRA 1 TI T (Bài s 2 )Ề Ể Ế ố
L p 11 ớ– Năm h c: 2013- 2014ọ
Môn: Hình h c Th i gian: 45 phútọ ờ
Câu 1. Trong mp Oxy, cho đi m ể
( )
2; 7A−
và đng tròn (C): ườ
( )
22
3 100x y+ + =
a) Tìm nh c a đi m A qua phép t nh ti n theo véc t ả ủ ể ị ế ơ
( 2;1)v−
r
b) Vi t ph ng trình đng tròn nh c a (C ) qua phép t nh ti n theo véc t ế ươ ườ ả ủ ị ế ơ
( 2;1)v−
r
.
Câu 2 . Vi t ph ng trình nh c a đng th ng ế ươ ả ủ ườ ẳ
:3 2 12 0d x y− − =
qua phép quay tâm
O góc
0
90
.
Câu 3.
a) Tìm nh c a tam giác ABC có ba góc nh n qua phép v t tâm H là tr c tâm c a tam ả ủ ọ ị ự ư ủ
giác ABC có t s v t ỉ ố ị ự
1
2
k=
b) Cho hình ch nh t ABCD tâm I. G i J, K,L l n l t là trung đi m c a BC,CJ và CI. ữ ậ ọ ầ ượ ể ủ
Ch ng minh hai hình thang IJKL và DCJI đng d ng.ứ ồ ạ
Câu 4.
a) Vi t ph ng trình (C’) là nh c a đng tròn(C): ế ươ ả ủ ườ
2 2 2 4 4 0x y x y+ + − − =
qua phép vị
t tâm O, t s k=2. Tìm t a đ tâm v t ngoài K c a hai đng tròn (C) và (C’)ự ỉ ố ọ ộ ị ự ủ ườ
b) Cho đi m A n m ngoài đng tròn (O;R) và hai đi m B,C thay đi trên (O) sao cho ể ằ ườ ể ổ
đ dài đo n th ng BC luôn b ng ộ ạ ẳ ằ
3R
. Tìm qu tích tr ng tâm G c a tam giác ABC.ỹ ọ ủ
………………………………………
H NG D N ĐÁP SƯỚ Ẫ Ố
1. G i A’(x’;y’) là nh c a A qua phép t nh ti n theo véc t ọ ả ủ ị ế ơ
( 2;1)v−
r
. Ta có: A(0;6)
b) (C) có tâm I(-3;0), bán kính R=10. G i (C’) là nh c a (C) qua phép t nh ti n theo véc ọ ả ủ ị ế
t ơ
( 2;1)v−
r
.
Khi đó(C’) có tâm I’ (-5;1), bán kính R’=R=10
V y ph ng trình (C’): ậ ươ
( )
22
5 ( 1) 100x y+ + − =
2. Đng th ng (d) c t tr c Ox, Oy l n l t t i A(4;0) và B(0;-6).ườ ẳ ắ ụ ầ ượ ạ
G i A’,B’ l n l t là nh c a A,B qua phép quay tâm O, góc quay 90ọ ầ ượ ả ủ 0. Khi đó: A’(0;4),
B’(6;0). Suy ra nh c a (d) qua phép quay tâm O, góc quay 90ả ủ 0 là đng th ng (d’) đi quaườ ẳ
hai đi m A’, B’. V y ph ng trình ể ậ ươ
3. a) D ng A’,B’,C’ l n l t là trung đi m c a HA,HB và HC. ự ầ ượ ể ủ
Ta có:
1 1 1
' ; ' ; ' .
2 2 2
HA HA HB HB HC HC= = =
uuuur uuur uuuur uuur uuuur uuur
Do đó phép v t tâm H , t s v t ị ự ỉ ố ị ự
1
2
k=
bi n tam ế
giác ABC thành tam giác A’B’C’ (HS t v hình)ự ẽ
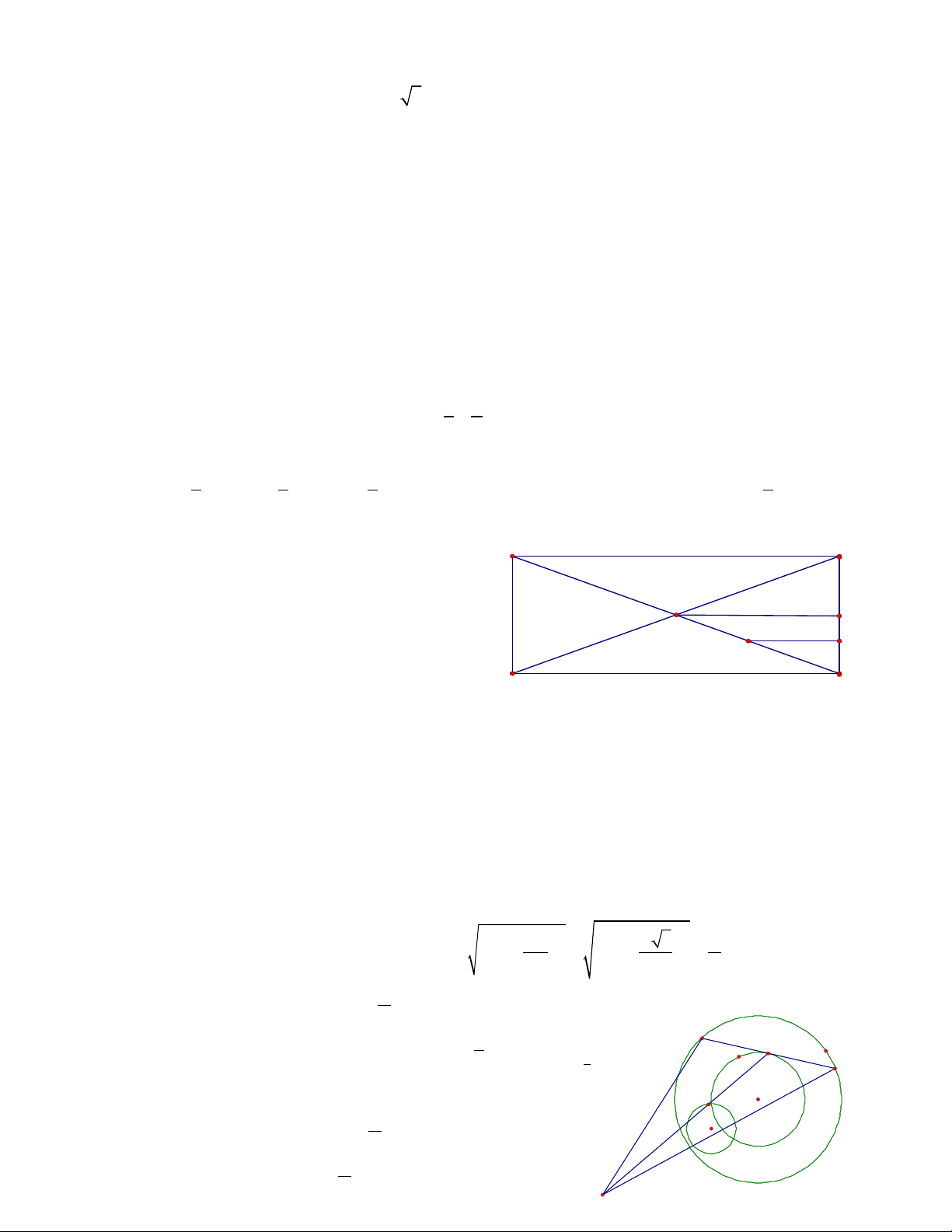
b) Ta có:
( )
( )
( )
( )
;2 IJ
;2 IJ
;2 IJ
;2 IJ
C
C
C
C
VD
VD
VD
VD
I A D
J B C
K J J
L I J
Phép đng d ng có đc b ng cách th c hi n liên ti p phép v t tâm C, t s k=2 và ồ ạ ượ ằ ự ệ ế ị ự ỉ ố
phép đi x ng tr c IJ bi n hình thang IJKL thành hình thang DCJI. V y hai hình thang ố ừ ụ ế ậ
IJKL và DCJI đng d ng.ồ ạ
4. a) (C) có tâm I(-1;2), bán kính R=3. G i (C’) là nh c a (C) qua phép v t tâm O, t sọ ả ủ ị ự ỉ ố
k=2. Khi đó (C’) có tâm I’ th a ỏ
( )
' 2 ' ' 2;4OI OI I= −�
uuur uuur
, bán kính R’=2R=6.
V y ph ng trình (C’) : ậ ươ
( )
22
2 ( 4) 36x y+ + − =
.
* t a đ tâm v t ngoài K c a hai đng tròn (C) và (C’) th a h th cọ ộ ị ự ủ ườ ỏ ệ ứ
( )
' 2 ' 0;0KI KI K=
uuur uuur
b) *G i I là trung đi m c a BC, ta có: ọ ể ủ
2
2
2 2 3
2 2 2
BC R R
OI R R � �
� �
= − = − =
� �
� � � �
� � � �
. Suy ra I ch y ạ
trên đng tròn tâm O, bán kính ườ
2
R
.
*Tr ng tâm G c a tam giác ABC th a ọ ủ ỏ
( )
2
;3
2
3A
AG AI G V I
� �
� �
� �
= =�
uuur uur
V y: qu tích tr ng tâm G c a tam giác ABC ậ ỹ ọ ủ
là đng tròn Tâm O’ bán kính ườ
3
R
là nh c a ả ủ
đng tròn tâm O, bán kính ườ
2
R
qua phép v t ị ự
J
I
A
D
B
C
K
L
O
A
O'
B
C
I
G
tâm A, t s k=2/3 . ỉ ố