
SỞ GD & ĐT TT HUẾ ĐỀ KIỂM TRA HỌC KÌ I - Năm học 2009-2010
TRƯỜNG THPT BÌNH ĐIỀN Môn: Toán 11
Thời gian: 90 phút ( không kể thời gian giao đề )
I. PHẦN CHUNG CHO CẢ HAI BAN (7 điểm)
Câu I: (2điểm): Giải các phương trình:
1.
sin 3 cos 0xx
2.
22
os 2 sin 2 0c x x
Câu II: (1,5 điểm) Một tổ trực có 9 học sinh nam và 4 học sinh nữ. Giáo viên chọn ra 3
học sinh.
Tính xác suất để:
1. Cả 3 học sinh cùng giới tính.
2. Có ít nhất 1 học sinh nữ.
Câu III: (1,5 điểm)
1. Tim giá trị lớn nhất và giá trị nhỏ nhất của hàm số :
(sinx-2cosx)(2sinx+cosx)-1y
2. Khai triển nhị thức:
6
1x
x
Câu IV: (2 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi
M, N lần lượt thuộc cạnh SB, SC sao cho
21
,
32
SM SN
SB SC
.
1. Tìm giao tuyến của hai mặt phẳng
()AMN
và
()SBD
, từ đó suy ra giao điểm P
của SD và mặt phẳng
()AMN
.
2. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng
()AMN
và chứng minh
BD song song với thiết diện đó.
II. PHẦN DÀNH CHO HỌC SINH TỪNG BAN (3 điểm)
A. Dành cho học sinh ban cơ bản:
Câu Va: (1 điểm) Cho cấp số cộng
n
u
với công sai d, có
314u
,
50
80u
. Tìm
1
u
và
d. Từ đó tìm số hạng tổng quát của
n
u
.
Câu VIa: (2 điểm) Trong mặt phẳng tọa độ Oxy :
1. Viết phương trình d' là ảnh của d:
2 3 6 0xy
qua phép đối xứng tâm O.
2. Viết phương trình (C') là ảnh của (C):
22
( 2) ( 3) 16xy
qua phép tịnh tiến theo
(1; 2)v
B. Dành cho học sinh ban nâng cao:
Câu Vb: (1 điểm) Có bao nhiêu số tự nhiên có 5 chữ số trong đó chữ số đứng sau phải
lớn hơn chữ số đứng trước.
Câu VIb:(2 điểm) Trong mặt phẳng tọa độ Oxy :
1. Viết phương trình d' là ảnh của d:
2 3 0xy
qua phép đối xứng tâm I(1;-2).
2. Viết phương trình (C') là ảnh của (C):
22
( 3) ( 4) 16xy
qua phép vị tự tâm O
tỉ số
1
2
.
3.
4. ĐÁP ÁN - THANG ĐIỂM CHẤM ĐÈ KIỂM TRA HỌC KỲ I
5. Môn: TOÁN 11 - NĂM HỌC 2009 - 2010.
Câu
Ý
Nội dung
Điểm
I
Giải các phương trình
1
sin 3 cos 0xx
sin 3 cos tan 3x x x
(vì cosx = 0 không thỏa phương trình)
0.5
,
3
x k k Z
Vậy nghiệm của phương trình đã cho là:
,
3
x k k
0.5
2
22
os 2 sin 2 0c x x
21 cos 2
cos 2 2 0
2
x
x
21 os2x
os 2 2 0
2
c
cx
0.25
2
2cos 2 cos2 - 3 0xx
(*)
0.25
Đặt
cos2 , -1;1t x t
, (*) trở thành:
2
2 3 0tt
t = -1 hoặc
3
2
t
(loại)
0.25
Với t = -1: ta
có
os2x = -1 2x= +k2 x= ,
2
c k k
Z
Vậy nghiệm của phương trình đã cho là:
,
2
x k k
0.25
II
Chọn 3 học sinh trong 13 học sinh có
3
13 286nC
0.25
1
Gọi A là biến cố: "Cả 3 học sinh cùng giới tính"
0.25

A xảy ra khi 3 học sinh chọn ra cùng nam hoặc cùng
nữ
33
94
88n A C C
( ) 4
() ( ) 13
nA
PA n
0.25
2
Gọi B là biến cố: "có ít nhất 1 học sinh nữ"
Khi đó:
B
là biến cố:"không có học sinh nữ nào được
chọn"
B
xảy ra khi 3 học sinh chọn ra là 3 học sinh nam:
3
9
( ) 84n B C
0.25
42
() 143
PB
0.25
101
( ) 1 ( ) 143
P B P B
0.25
III
1
Ta có:
33
1 sin 2 2cos 2 sin 2 2cos 2 1 0
22
y x x x x y
(*)
0.25
(*) có nghiệm
2
2
2
2
321
2
4 8 21 0
73
22
y
yy
y
0.25
Giá trị lớn nhất và giá trị nhỏ nhất của y theo thứ tự là
3
2
và
7
2
0.25
2
66
01
66
5
2 2 3 3 4 4 5 5 6 6
6 6 6 6 6
4 3 2
1 1 1 .
1 1 1 1
. . . .
x C C x
x x x
C x C x C x C x C x
x x x x
0.5
2 4 6
6 4 2
1 1 1
6 15 20 15 6x x x
x x x
0.25
O
P
I
A
B
C
D
M
N
S
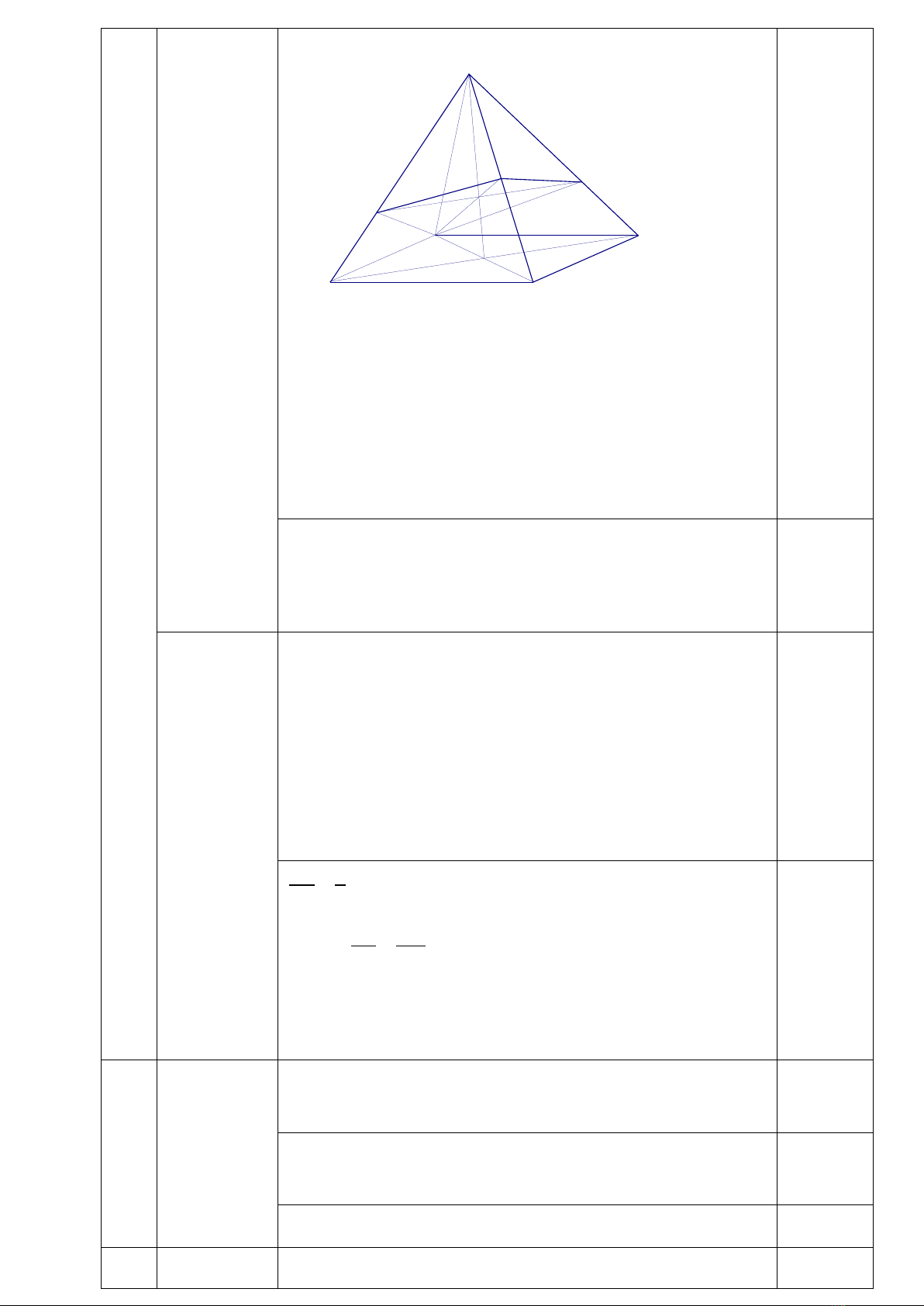
IV
1
Gọi I là giao điểm của SO và AN.
M, I là hai điểm chung của hai mặt phẳng (AMN) và
(SBD)
Suy ra
( ) ( )AMN SBD MI
0.5
Trong mp (SBD), MI cắt SD tại P thì
P SD
và
()P MI AMN
Do đó P là giao điểm của SD và mp (AMN)
0.5
2
Ta có
( ) ( )AMN SAB AM
( ) ( )AMN SBC MN
( ) ( )AMN SCD NP
( ) ( )AMN SDA PA
Thiết diện của hình chóp cắt bởi (AMN) là tứ giác
AMNP
0.5
2
3
SI
SO
(vì I là trọng tâm tam giác SAC)
Suy ra
//
SI SM MI BO
SO SB
hay MP//BD
Mà
()MP AMNP
Vậy BD//(AMNP)
0.5
Va
Ta có:
1
1
2 14
49 80
ud
ud
0.5
118
2
u
d
0.25
Vậy
18 ( 1).2
n
un
= -20 + 2n
0.25
VIa
1
Gọi
( ; ) , '( '; ')M x y d M x y
là ảnh của M qua phép đối
0.5

xứng tâm O thì
''Md
với d' là ảnh của d qua phép đối
xứng tâm O
''
''
x x x x
y y y y
d':
2( ') 3( ') 6 0xy
Vậy d':
2 3 6 0xy
0.5
2
Gọi
( ; ) ( ), '( '; ')M x y C M x y
là ảnh của M qua phép
tịnh tiến theo vectơ
v
Ta có
'1
'2
xx
yy
0.5
(C'):
22
( 3) ( 5) 16xy
0.5
Vb
Gọi số tự nhiên có 5 chữ số là
abcde
vì
a b c d e
nên các chữ số a,b,c,d,e được chọn trong các chữ số 1
đến 9.
0.5
Chọn 5 số khác nhau từ 9 số
1;2;...;9
có
5
9126C
cách
Với mỗi cách chọn ra chỉ lập được 1 số thỏa yêu cầu.
Vậy có 126 số cần tìm.
0.5
VIb
1
Gọi
( ; ) , '( '; ')M x y d M x y
là ảnh của M qua phép đối
xứng tâm I thì
''Md
với d' là ảnh của d qua phép đối
xứng tâm I
0.5
' 1.2 2 '
' 2.2 4 '
x x x x
y y y y
Vậy d':
2 11 0xy
0.5
2
(C) có tâm I(-3;4); bán kính R=4
Gọi I'(x';y'), R' là tâm và bán kính của (C')
Với (C'), I' là ảnh của (C) và I qua phép vị tự tâm O tỉ
số -1/2
0.25
Ta có:
1
'2
OI OI
nên:
3
'2
'2
x
y
và R'=2
0.5


![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)








