
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ KI M TRA CH T L NG H C KỲ IỂ Ấ ƯỢ Ọ
Đ NG THÁPỒNăm h c: 2012-2013ọ
Môn thi: TOÁN- L p 12ớ
Th i gian: 120 phút (ờkhông k th i gian phát để ờ ề)
Ngày thi: …../12/2012
Đ Đ XU TỀ Ề Ấ
(Đ g m có 01 trang)ề ồ
Đ n v ra đ : THPT L p Vò 1ơ ị ề ấ
A. PH N CHUNG CHO T T C H C SINH: (7,0 đi m)Ầ Ấ Ả Ọ ể
Câu I: (3,0 đi m)ể
Cho hàm s ố
3 2
3 4y x x= − + −
(C)
1/ Kh o sát và v đ th (C) c a hàm s .ả ẽ ồ ị ủ ố
2/ D a vào đ th (C) bi n lu n s nghi m ph ng trình ự ồ ị ệ ậ ố ệ ươ
3 2
3 0x x m− + =
.
Câu II (2.0 đi m)ể
1. Tính giá tr c a bi u th c ị ủ ể ứ
5
3
52 32
1
125
1
log8log
−
−+=M
2. Tìm giá tr l n nh t và giá tr nh nh t c a hàm s ị ớ ấ ị ỏ ấ ủ ố
xxxfy ln.)( ==
trên đo n [1 ; eạ2]
Câu III: (2,0 đi m)ể
Cho hình chóp S.ABCD có đáy ABCD là hình vuông c nh a, c nh ạ ạ SA vuông góc
v i ớmp (ABCD), c nh bên SC = 2ạa.
1/ Tính th tích kh i chóp ể ố S.ABCD.
2/ Tìm tâm và bán kính m t c u ngo i ti p hình chópặ ầ ạ ế S.ABCD.
II. PH N T CH N (3,0 đi m)Ầ Ự Ọ ể
H c sinh ch đ c ch n m t trong hai ph n sau đ làmọ ỉ ượ ọ ộ ầ ể
1. Ph n 1ầ
Câu IVa. (1,0 đi m) ểCho hàm s ố
2 1
1
x
yx
−
=−
có đ th (C). Vi t ph ng trình ti pồ ị ế ươ ế
tuy n v i (C) bi t ti p tuy n song sog v i đ ng th ng (d):ế ớ ế ế ế ớ ườ ẳ
xy −= 2013
Câu Va: (2,0 đi m)ể
1/ Gi i ph ng trình: ả ươ
1
4 16 3
x x+
− =

2/ Gi i b t ph ng trình: ả ấ ươ
1
2
3 1
log 1
2
x
x
−
≤ −
÷
− +
2. Ph n 2ầ
Câu IVb. (1,0 đi m)ể Cho hàm s ố
2 1
1
x
yx
−
=−
có đ th (C). Vi t ph ng trình ti pồ ị ế ươ ế
tuy n v i (C) bi t ti p tuy n vuông góc v i đ ng th ng (d): ế ớ ế ế ế ớ ườ ẳ
2013
4
1+= xy
.
Câu Vb: (2,0 đi m)ể
1. Cho hàm s ố
( 1)
x
y x e= +
. Ch ng t r ng: ứ ỏ ằ
'
x
y y e− =
2. Tìm các giá tr c a k sao cho đ ng th ng (d):ị ủ ườ ẳ
y kx=
ti p xúc v i đ ngế ớ ườ
cong (C):
3 2
3 1y x x= + +
.
H tế

H NG D N CH M Đ Đ XU TƯỚ Ẫ Ấ Ề Ề Ấ
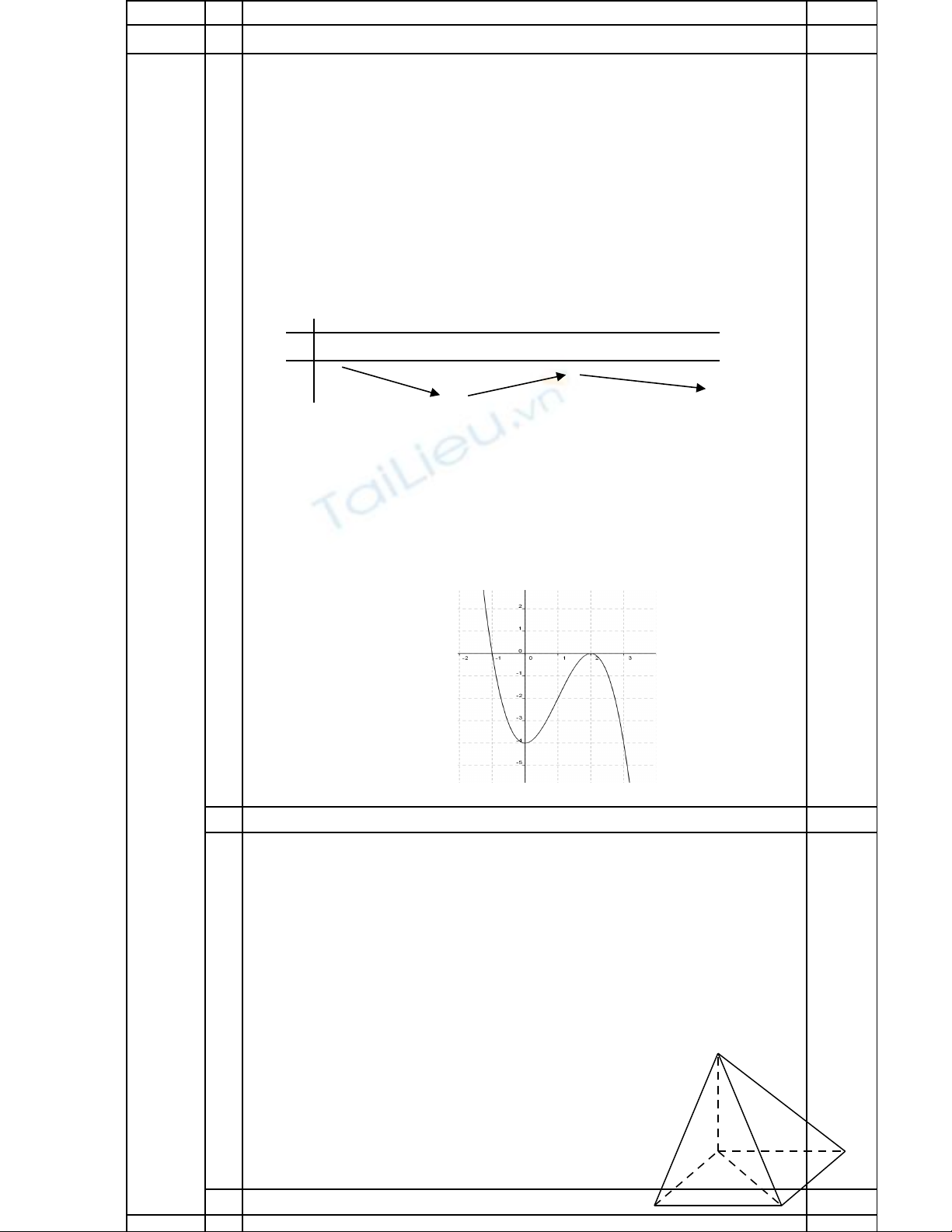
Câu Ý N i dungộĐi mể
I 1Kh o sát và v đ th (C) c a hàm s ả ẽ ồ ị ủ ố
3 2
3 4y x x= − + −
(C) 2đ
•T p xác đ nhậ ị :
D R=
•Gi i h nớ ạ :
lim
x
y
→−∞
= +∞
;
lim
x
y
→+∞
= −∞
•S bi n thiên:ự ế
2
3 6y x x
′= − +
2
0 4
0 3 6 0 2 0
x y
y x x x y
= = −
′= ⇔ − + = ⇔ ⇔
= =
•B ng bi n thiên:ả ế
Hàm s đ ng bi n trong kho ng ố ồ ế ả
( )
0; 2
Hàm s ngh ch bi n trong kho ng ố ị ế ả
)0;(−∞
và
);2( + ∞
.
Hàm s đ t c c đ i t i ố ạ ự ạ ạ
2; 0
CD
x y= =
Hàm s đ t c c ti u t i ố ạ ự ể ạ
0; 4
CT
x y= = −
•Đ th :ồ ị
* Giao đi m c a đ th v i tr c Oy là (0 ; 4)ể ủ ồ ị ớ ụ
* Giao đi m c a đ th v i tr c Ox là (-1 ; 0) và (2 ; 0)ể ủ ồ ị ớ ụ
* Đi m u n: ể ố
(1; 2)I−
0.25
0.25
0.25
0.25
0.25
0.25
0.5
2Bi n lu n s nghi m ph ng trình ệ ậ ố ệ ươ
3 2
3 0x x m− + =
(1) 1.0 đ
* Ta có:
3 2
3 0x x m− + =
3 2
3 2
3
3 4 4
x x m
x x m
⇔ − + =
⇔ − + − = −
Đây là ph ng trình hoành đ giao đi m c a đ th (C) vàươ ộ ể ủ ồ ị
đ ng th ng ườ ẳ
y = m – 4. S giao đi m chính là s nghi m ph ng trình (1).ố ể ố ệ ươ
•
4 4 0
4 0 4
m m
m m
− < − <
⇔
− > >
Có m t giao đi m. Ph ng trình (1) cóộ ể ươ
m t nghi m.ộ ệ
•
4 4 0
4 0 4
m m
m m
− = − =
⇔
− = =
Có hai giao đi m. Ph ng trình (1) có haiể ươ
nghi m.ệ
•
4 4 0 0 4m m
− < − < ⇔ < <
Có ba giao đi m. Ph ng trình (1) cóể ươ
ba nghi m.ệ
0.25
0.25
0.25
0.25
II 2đ
x
y’
y
0 2
- 0 + 0 -
-4 0
+∞
S
A
BC
D
2
a
a
aa











![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)




