
C©u I.
1) Cho hµm sè
f(x) = 3533615362412
42 2
cos cos sin cos .xx xx aa−− −++−
Víi gi¸ trÞ nµo cña a th× f(x) >0 víi mäi x ?
2) X¸c ®Þnh tham sè a ®Ó hÖ ph ¬ng tr×nh sau cã nghiÖm :
xya
xy a
++ + =
+=
12
3
C©u II.
1) Tam gi¸c ABC cã c¸c c¹nh víi ®é dµi a, b, c, vµ cã diÖn tÝch S. §ûêng trßn néi tiÕp cña tam gi¸c tiÕp xóc víi c¸c
c¹nh ë A’, B’, C’ (®èi diÖn víi c¸c ®Ønh A, B, C). Tam gi¸c A’B’C’ cã c¸c c¹nh a’, b’, c’, vµ diÖn tÝch S’. Chûáng minh
c¸c ®¼ng thûác sau :
i) a'
a+b'
b=2sin
C
2sin A
2+sin
B
2
;
ii) S'
S=2sin
A
2sin B
2sin C
2.
2) Chøng minh r»ng víi mäi x, ta ®Òu cã
cos3x + asin3x + 1
cos3x + 2
1+ 1+3a
3
2
≤.
C©u III. Cho a, b, c, d >0. Chûáng minh r»ng
1<a
a+b+c+b
b+c+d +c
c+d+a +d
d+a+b <2
.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
C©u I.
1) BiÕn ®æi hµm sè:
f(x) = 3cos4x - 5(4cos3x - 3cosx) - 36(1 - cos2x) - 15cosx++36+24a-12a
2.
f(x) = 3cos4x - 20cos3x + 36cos2x + 24a - 12a2.
§Æt t = cosx, (|t| £1) vµ xÐt hµm: ϕ(t)=3t
4- 20t3+ 36t2+ 24a - 12a2.
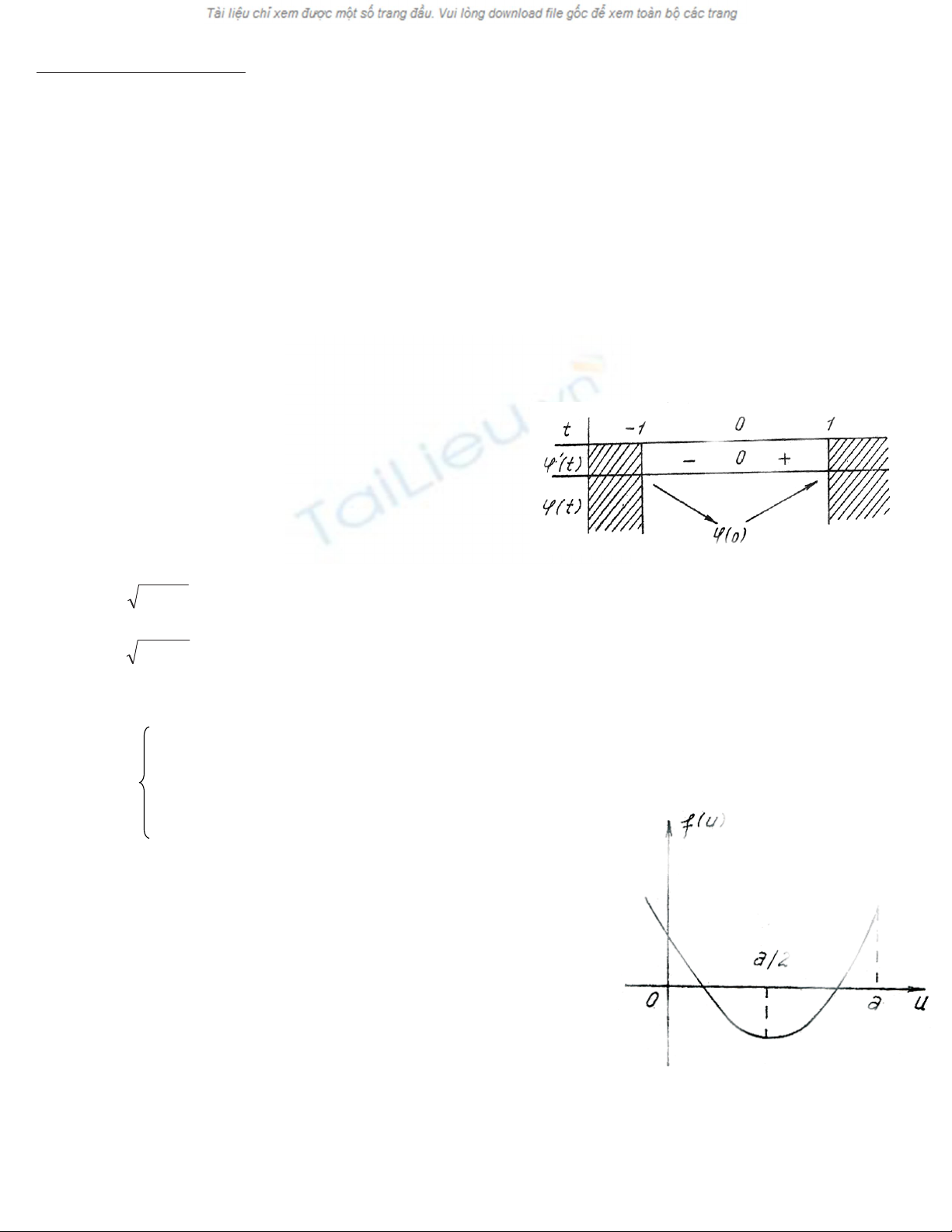
T×m a ®Ó víi "tÎ[-1;1]ta®Òucãj(t)>0.Tacã:
ϕ‘(t) = 12t3- 60t2+ 72t = 12t (t2-5t+6).
ϕ(0) = 24a - 12a2.
Muèn j(t)>0víi"tÎ[-1;1]th×cÇnvµ®ñlµ:
24a - 12a2>0Û0<a<2.
2) §Æt : u= x+1
,(u³0);
v= y+2
,(v³0)
Th× u2+v
2=x+y+3.Do vËy, hÖ ®· cho ®ûîc thay bëi hÖ míi:
u+v=a (1)
u2+v
2=3(a+1)(2)
u,v³0. (3)
NhËn thÊy ngay nÕu a £0 th× hÖ v« nghiÖm. VËy chØ cÇn xÐt
a>0.ThÕ v=a-uvµo (2) sÏ ®ûîc:
2u2-2au+(a
2-3a-3)=0. (4)
§Ó hÖ cã nghiÖm th× cÇn vµ ®ñ lµ (4) cã nghiÖm uÎ[0;a]
(chó ý u+v=a).
www.khoabang.com.vn LuyÖn thi trªn m¹ng
________________________________________________________________________________
Ta tíi:∆‘³0
2f(0) ³0
víi
f(u) = 2u2-2au+(a
2-3a-3);
∆‘=a
2- 2(a2-3a-3)=-a
2+6a+6.
VËy ∆‘³0víi 3+ 15 ³a³↔3- 15.
f(0) = a2-3a-3³0Ûa£3- 21
2hoÆc a³3+ 21
2.
Do xÐt a>0nªn cuèi cïng ta ®ûîc: 3+ 15 a 3+ 21
2
≥≥ .
C©u II.
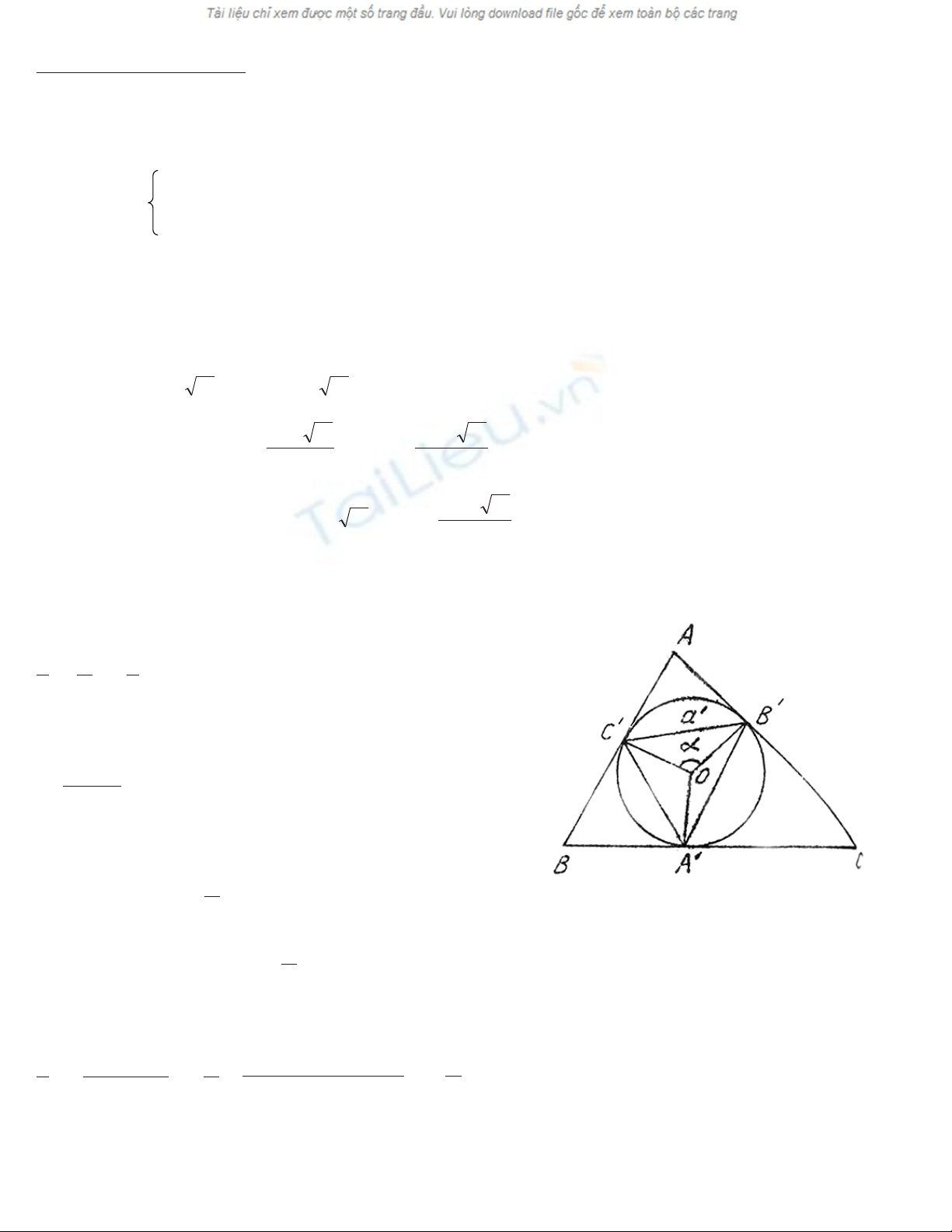
1) i) Chó ý r»ng:
πα
2-A
2=2= A’.
Do ®ã:
sin B+C
2= sinA’.
Ta cã:
a‘ = 2rsinA’ = 2(p-a)tg A
2sinA’=
=(b+c-a)tg=(b + c - a) sin A
2.
Do vËy:
a'
a=b+c-a
asin A
2=sinB + sinC - sinA
sinA sin A
2
=
www.khoabang.com.vn LuyÖn thi trªn m¹ng
________________________________________________________________________________

=
2sin B+C
2cos B-C
2-2sin
A
2cos A
2
2cos A
2
=
2cos A
2cos B-C
2-cos
B+C
2
2cos A
2
=2sin B
2sin C
2.
VËy : a'
a=2sin
B
2sin C
2. (1)
Tû¬ng tù : b'
b=2sin
A
2sin C
2.(2)
Tõ (1) vµ (2) suy ra:
a'
a+b'
b=2sin
C
2sin A
2+sin
B
2
S'
S=
1
2a' b'sinC'
1
2absinC
=a'
a.b'
b.
sin A+B
2
sinC = 4sin2C
2sin A
2sin B
2.
cos C
2
2sin C
2cos C
2
=2sin A
2sin B
2sin C
2.
2) XÐt hµm sè:
y=cos3x + asin3x + 1
cos3x + 2 .
Sè yothuéc miÒn gi¸ trÞ cña hµm sè Êy khi vµ chØ khi phû¬ng tr×nh:
yo=cos3x + asin3x + 1
cos3x + 2 (1) cã nghiÖm:
(1) Ûyo(cos3x + 2) = cos3x + asin3x + 1
Û(- yo+ 1)cos3x + asin3x+1-2y
o= 0. (2)
(2) cã nghiÖm khi vµ chØ khi:
(1-y
o)2+a
2³(2yo-1)
2Û3yo
2-2y
o-a
2£0Û
1- 1+ 3a
3y1+ 1+3a
3
2
o
2
≤≤ .
www.khoabang.com.vn LuyÖn thi trªn m¹ng
________________________________________________________________________________

Tõ ®ã suy ra, víi mäi x ta ®Òu cã:
cos3x + asin3x + 1
cos3x + 2
1+ 1+3a
3
2
≤.
C©u III.
Trûúác hÕt, ta chøng minh r»ng : nÕu0<T<Mvµ α>0th× ta cã:
T
M<T+
M+
α
α. (1)
Thùc vËy:
(1) ÛT(M + α) < M(T + α)ÛTα<MαÛT<M.
¸p dông:
i) S'
S=
1
2a' b'sinC'
1
2absinC
=a'
a.b'
b.
sin A+B
2
sinC =
a
a+b+c+d<a
a+b+c<a+d
a+b+c+d
. (2)
Tû¬ng tù cã:
b
a+b+c+d <b
b+c+d <b+a
b+c+d+a ; (3)
c
a+b+c+d <c
c+d+a <c+b
c+d+a+b; (4)
d
a+b+c+d <d
d+a+b <d+c
d+a+b+c. (5)
Céng theo vÕ (2), (3), (4) vµ (5):
1< a
a+b+c +b
b+c+d +c
c+d+a+d
d+a+b<2.
www.khoabang.com.vn LuyÖn thi trªn m¹ng
________________________________________________________________________________
















