www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
C©u I. Cho hµm sè
y=2x + (1 - m)x + 1 + m
x-m
2
. (1)
1)Víim=1,h·ykh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ cña hµm sè.
2) Chøng minh r»ng víi mäi m¹-1, ®å thÞ hµm sè (1) lu«n tiÕp xóc víi mét ®ûêng th¼ng cè ®Þnh t¹i mét ®iÓm cè
®Þnh.
3) X¸c ®Þnh m ®Ó hµm sè (1) lµ ®ång biÕn trªn kho¶ng (1;+¥).
C©u II.
1) Chøng minh r»ng víi 5 sè a, b, c, d, e bÊt k×, bao giê ta còng cã
a2+b
2+c
2+d
2+e
2³a(b+c+d+e).
2) Cho a £6,b£-8,c£3. Chøng minh r»ng víi mäi x ³1 ta ®Òu cã
x4-ax
2-bx³c.
C©u III. 1) Gi¶i phû¬ng tr×nh
2 cos23x
5+1=3cos4x
5.
2) Chøng minh r»ng trong mäi tam gi¸c ABC ta ®Òu cã
2(sinA sin2A + sinB sin2B + sinC sin2C) < (sinA + sinB + sinC)(sin2A + sin2B + sin2C).
www.khoabang.com.vn LuyÖn thi trªn m¹ng
___________________________________________________________________
C©u I.
1) §Ò nghÞ tù gi¶i.
2) Tr−íc hÕt t×m ®iÓm cè ®Þnh A oo
(x , y ) sao cho (1) qua A víi ∀m ≠ − 1. Khi ®ã
2
oo
oo
2x (1 m)x 1 m
yxm
+− ++
=−, ∀m ≠ −1
⇒ 2
oo o o
y(x m) 2x (1 m)x 1 m−= +− ++ (∀m) ⇔ 2
oo oo oo
(x y 1)m y x 2x x 1 0
−
−+ −−−= (∀m)
⇒ oo
2
oo o o
xy1
yx 2x x 1 0
−=
−−−=
Gi¶i hÖ ®ã ta ®−îc o
x1=− , o
y2=− .
DÔ kiÓm tra r»ng m ≠ − 1 (1) ®Òu qua (−1, −2).
MÆt kh¸c
22
2
2x 4mx m 2m 1
y'(x) (x m)
−+−−
=− ;
2
2
(m 1)
y'( 1) 1
(m 1)
+
−
==
+ víi ∀m ≠ −1.
Tõ ®ã ta thÊy, c¸c ®−êng cong (1) ®Òu tiÕp xóc víi ®−êng th¼ng y = x − 1 t¹i (−1, −2).
3) Muèn hµm ®ång biÕn trong kho¶ng 1 < x < + ∞ th× ta cÇn chän m sao cho
22
2
2x 4mx m 2m 1 0
(x m)
−+−−
≥
−
víi 1 < x < + ∞ ⇔
22
2x 4mx m 2m 1 0−+−−≥ trong (1 ; + ∞)
m ≤ 1
§Æt 22
f(x) 2x 4mx m 2m 1=− +−− ; ∆' 22 2
4m 2m 4m 2 2(m 1) 0
=
−++=+≥.
NÕu m = −1 th× tháa m·n.
NÕu m ≠ −1 ta cÇn cã
2f(1) 0
4m 1
4
≥
<
⇔
2
m6m10
m1
−
+≥
<
⇔ m322≤− .
KÕt luËn : m322≤− .
C©u II.
1) 22222
abcde++++
≥ a(b + c + d + e) ⇔
⇔22
22
aa
babcac
44

+− + +− +


22
22
aa
dadeae0
44

+− + +− ≥


⇔
22 2
2
aaaa
bcde0
2222


−+−+−+−≥


.
2) §Æt 42
f(x) x ax bx=− −.
Ta cã : f'(x) = 4 3
x − 2ax − b,
f''(x) = 12 2
x − 2a = 2(6 2
x − a). Do a ≤ 6 vµ 2
x ≥ 1 nªn f''(x) ≥ 0 ⇒ f'(x) ®ång biÕn trong kho¶ng [1 ; + ∞).
f'(1) = 4 − (2a + b) ≥ 0 (do 2a + b ≤ 4).
VËy f'(x) ≥ 0 trong kho¶ng [1 ; + ∞) ⇒ f(x) ®ång biÕn trong kho¶ng ®ã. L¹i cã
f(1) = 1 − (a + b) ≥ 3 (do a + b ≤ −2).
VËy víi mäi x ∈ [1 ; + ∞) ta ®Òu cã f(x) ≥ 3 ≥ c
(®iÒu ph¶i chøng minh).
www.khoabang.com.vn LuyÖn thi trªn m¹ng
___________________________________________________________________
C©u III.
1) §Æt 2x
cos t (| t | 1)
5=≤
ta sÏ tíi
32
4t 6t
−
− 3t + 5 = 0
hay (t − 1)(4 2
t − 2t − 5) = 0.
Ph−¬ng tr×nh nµy cã hai nghiÖm 1
t1=, 2121
t4
−
= thÝch hîp, cßn nghiÖm 3121
t4
+
= > 1 bÞ lo¹i.
Tõ ®ã t×m ra x.
2) BÊt ®¼ng thøc cÇn chøng minh t−¬ng ®−¬ng víi
0 < sinA(−sin2A + sin2B + sin2C) + sinB(sin2A − sin2B + sin2C) + sinC(sin2A + sin2B − sin2C).(1)
Ta cã :
−sin2A + sin2B + sin2C = −2sinAcosA + 2sin(B + C)cos(B − C) = 2sinA[cos(B + C) + cos(B − C)]
= 4sinAcosBcosC,
vËy (1) t−¬ng ®−¬ng víi
2
acosBcosC + 2
bcosAcosC + 2
ccosAcosB > 0. (2)
NÕu ABC lµ tam gi¸c nhän hay vu«ng th× (2) hiÓn nhiªn ®óng. Gi¶ thö ABC lµ tam gi¸c tï, ch¼ng h¹n cã gãc A
tï. ThÕ th×
222 22
abc2bccosAbc=+− >+, do vËy (cosB, cosC > 0)
2
acosBcosC + 2
bcosAcosC + 2
ccosAcosB > 22
(b c )+cosBcosC + 2
bcosAcosC + 2
ccosAcosB =
2
bcosC(cosA + cosB) + 2
ccosC(cosA + cosC) > 0
bëi v× dÉu cosA < 0 nh−ng
cosA + cosB = AB AB
2cos cos
22
+
− > 0.
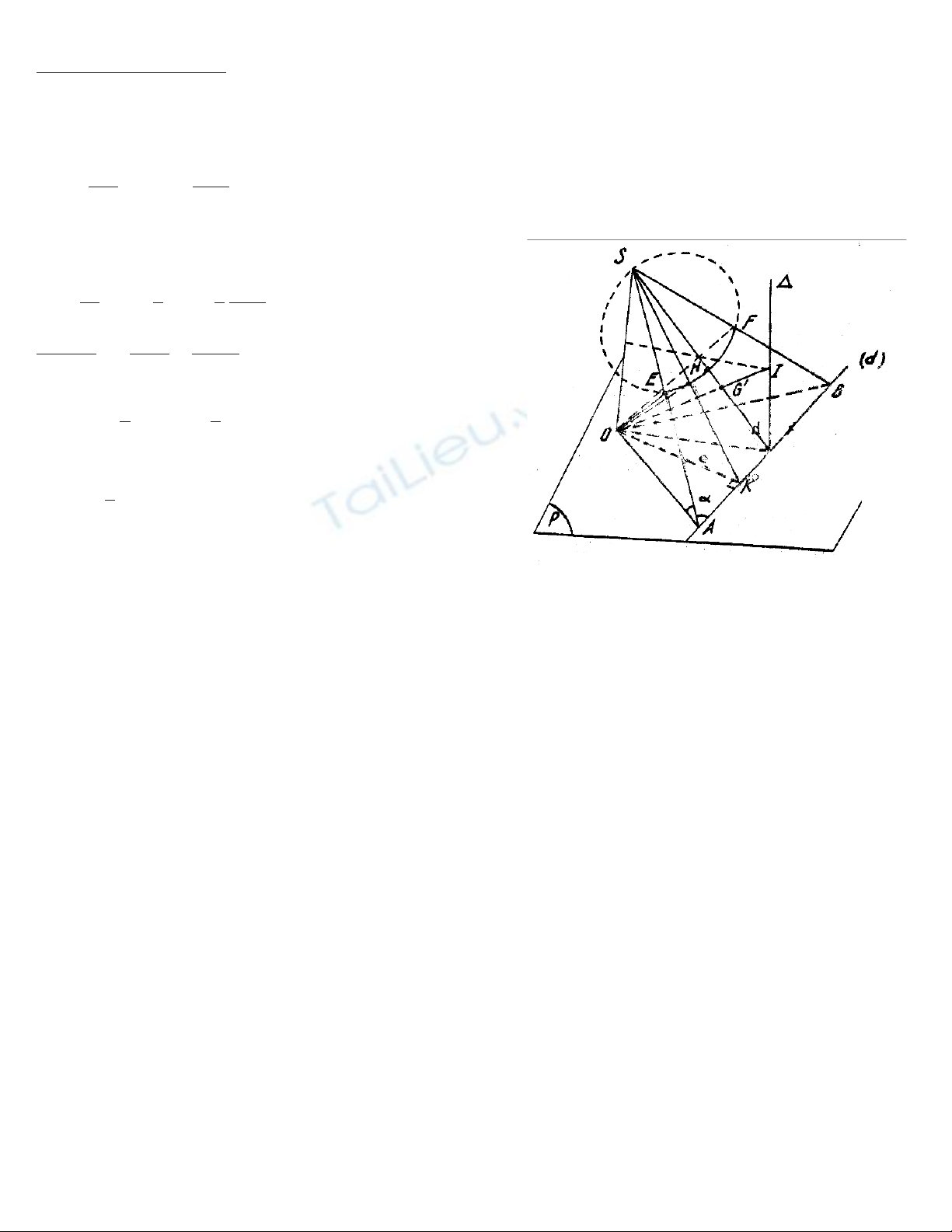
C©u IVb. 1) Gäi K lµ ch©n ®ûêng vu«ng gãc h¹ tõ O xuèng (d). Ta cã:
sina=OK
OA ÞOA = a
sina.
Trong tam gi¸c vu«ng SOA ta cã :SA
2=SO
2+OA
2.Nhûng
SO = 8
3
a;SA=5
3OA = 5
3
a
sina.VËy
25
9
64
9
2
222
2
aaa
sin sinaa
=+ Þ25 = 64sin2x+9
Ûsin 2a=1
4Þ=Þ=sinaa
1
2300(ë ®©y ta kh«ng lÊy gi¸ trÞ
sina=-1
2v× alµ mét gãc trong tam gi¸c).
2) §o¹n SO cè ®Þnh,OES OFC
^^
==90
o. §iÓm E vµ F di chuyÓn
nhûng lu«n lu«n nh×n ®o¹n cè ®Þnh SO d íi mét gãc vu«ng, do
®ã E vµ F n»m trªn mÆt cÇu ®ûêng kÝnh SO.
MÆt kh¸c E vµ F di chuyÓn nhûng lu«n lu«n n»m trong mÆt ph¼ng (S, d) cè ®Þnh. VËy E vµ F n»m trªn giao tuyÕn cña
hai mÆt nãi trªn. Giao tuyÕn Êy lµ mét ®ûêng trßn, kÝ hiÖu lµ (g), n»m trong mÆt ph¼ng (S, d).
H¹ OH ^SK ta cã H thuéc mÆt cÇu ®ûêng kÝnh SO.
MÆt ph¼ng (SOK) lµ mÆt ®èi xøng cña h×nh cÇu ®ûêng kÝnh SO. Ta l¹i cã mÆt ph¼ng (S, d) vu«ng gãc víi mÆt
ph¼ng(SOK). Do ®ã ®ûêng trßn (g) n»m trong mÆt ph¼ng (S, d) ph¶i nhËn SK lµm trôc ®èi xøng. Do H còng thuéc (g)
nªn SH chÝnh lµ ®ûêng kÝnh cña ®ûêng trßn ®ã.
§¶o l¹i : LÊy mét ®iÓm F trªn (g), F kh¸c S vµ kh¸c H. Nèi SF, v× SF thuéc mÆt ph¼ng (S, d) do ®ã SF kÐo dµi c¾t (d)
ë B. Nèi OB,dùng gãc vu«ng BOA
^
trong mÆt ph¼ng P (A trªn d). Nèi SA, nã c¾t ®ûêng trßn (g) t¹i E. V× E, F n»m
trªn (g) nªn E, F n»m trªn mÆt cÇu ®ûêng kÝnh SO, do ®ã OE ^SA, OF ^SB.
VËy tËp hîp c¸c ®iÓm E vµ F lµ ®ûêng trßn (g) - giao cña mÆt cÇu ®ûêng kÝnh SO vµ mÆt ph¼ng (S, d) - trõ hai ®iÓm S
vµ H.
www.khoabang.com.vn LuyÖn thi trªn m¹ng
_______________________________________________________________________________
3) Gäi M lµ ®iÓm gi÷a cña AB. V× tam gi¸c AOB vu«ng ë O nªn M chÝnh lµ t©m ®ûêng trßn ngo¹i tiÕp tam gi¸c ®ã.
T©m I cña h×nh cÇu ngo¹i tiÕp tø diÖn SOAB ph¶i n»m trªn giao cña mÆt ph¼ng trung trùc R cña ®o¹n SO víi ®ûêng
th¼ng (D) vu«ng gãc víi P t¹i ®iÓm M. Do ®ã ta cã MI//SO vµ SO = 2MI.
Nèi OI, nã gÆp trung tuyÕn SM cña tam gi¸c SAB t¹i G’:
Ta cã :G'M
G'S =MI
SO =1
2ÞG'M
SM =1
3.
VËy G’ trïng víi t©m G cña tam gi¸c SAB. Hay nãi c¸ch kh¸c ba ®iÓm O, G, I lµ th¼ng hµng.
www.khoabang.com.vn LuyÖn thi trªn m¹ng
_______________________________________________________________________________