
UBND HUYỆN QUẾ SƠN
PHÒNG GIÁO DỤC - ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP HUYỆN
NĂM HỌC 2017-2018
Môn: Toán
Thời gian làm bài: 150 phút (Không kể thời gian giao đề)
ĐỀ CHÍNH THỨC - VÒNG II
Bài 1 (3,0 điểm):
Cho ba số thực a, b, c thỏa .
a) Chứng minh .
b) Tính khi có thêm điều kiện
2 2 2 6abc
.
Bài 2 (4,0 điểm):
Tam giác ABC có số đo các cạnh là: a, b, c. Gọi là chu vi của tam giác. Chứng
minh rằng :
a)
b)
c) Cho 2p = 18. Tìm giá trị nhỏ nhất của
Bài 3 (4,0 điểm):
Cho phương trình: . Thực hiện:
a) Giải phương trình với m = 9.
b) Tìm m để phương trình có bốn nghiệm phân biệt thỏa:
Bài 4 (7,0 điểm):
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M
khác B, C). Trên cạnh AB lấy điểm N sao cho BN = CM. Tia AM cắt đường thẳng
CD tại E.
a) Chứng minh ∆OMN là tam giác vuông cân.
b) Chứng minh MN // BE.
c) Gọi H là giao điểm của OM với BE. Chứng minh CH vuông góc với BE.
Bài 5 (2,0 điểm):
Tìm nghiệm nguyên của phương trình:
====HẾT====
0a b c
4 4 4 2 2 2 2 2 2
2a b c a b b c c a
4 4 4
abc
2p
1 1 4
a b a b
1 1 1 1 1 1
2
p a p b p c a b c
2 2 2
abc
21 3 5x x x m
1 2 3 4
, , ,x x x x
1 2 3 4
1 1 1 1 1
x x x x
22
2 4 3 19x x y

UBND HUYỆN QUẾ SƠN
PHÒNG GIÁO DỤC - ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP HUYỆN
NĂM HỌC 2017-2018
HƯỚNG DẪN CHẤM MÔN TOÁN VÒNG II
Bài 1 (3,0 điểm):
Từ được:
0,25
0,25
0,25
0,50
Thay a + b + c = 0 được:
0,25
0,50
Từ và
được:
Thay được
2
4 4 4 618
2
abc
0,75
0,25
Bài 2 (4,0 điểm):
(Do a > 0, b >0 nên ab(a+b)>0)
0,25
0,50
0,25
Áp dụng a) được:
1 1 4 4
2p a p b p a b c
;
1 1 4 4
2p a p c p a c b
;
1 1 4 4
2p b p c p b c a
0,50
0,25
Cộng được:
1 1 1 4 4 4
2( )
1 1 1 1 1 1
2( )
p a p b p c c b a
p a p b p c c b a
0,25
0,25
Có
2 2 2 2 2 2
2 ; 2 ; 2a b ab b c bc a c ac
0,50
Cộng được:
2 2 2
2( ) 2 2 2a b c ab ac bc
2 2 2 2 2 2
3( ) 2 2 2a b c a b c ab ac bc
0,25
0,25
0,25
0a b c
2 2 2
2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2
2 2 2 0
( ) 4( )
( ) 4( )
( ) 4( ( ))
a b c ab ac bc
a b c ab ac bc
a b c a b a c b c a bc b ac c ab
a b c a b a c b c abc a b c
2 2 2 2 2 2 2 2 2 2
4 4 4 2 2 2 2 2 2
( ) 4( )
2( )
a b c a b a c b c
a b c a b a c b c
2 2 2 2 2 2 2 2 2 2
( ) 4( )a b c a b a c b c
4 4 4 2 2 2 2 2 2
2a b c a b b c c a
2 2 2 2
4 4 4 ()
2
abc
abc
1 1 4 4ab
a b a b ab a b
2
( ) 4a b ab
2
( ) 0ab

2
2
2 2 2 2
()
33
p
abc
abc
2 2 2
abc
có giá trị nhỏ nhất là 182: 3 = 108 khi
abc
= 6.
0,50
Bài 3 (4,0 điểm):
0,50
Đặt y = được:
0,50
0,25
được và
0,25
Từ phương trình (*). Đặt y = được
0,50
(*)
0,50
Do ; có vai trò như nhau trong biểu thức.
Gọi là hai nghiệm của phương trình:
(1)
Có: .
0,50
và là hai nghiệm của phương trình:
(2)
Có: .
0,25
Thay vào (*) được:
0,50
Với m = -7 thì (*) có 4 nghiệm phân biệt. Kết luận m = -7.
0,25
Bài 5 (2,0 điểm):
0,50
0,25
Do nên
0,50
Xét : y = 0; y = ±1; y = ±2
0,25
Do là số chẵn là số chẵn y = ±1
0,25
Được nghiệm (2; 1 ) ; (2 ; -1) ; (-4, 1) ; (-4 ; -1)
0,25
22
1 ( 1) 3 5 9
( 4 5)( 4 3) 9
x x x x
x x x x
241xx
2
( 4)( 4) 9 25 5 à 5y y y y v y
22
4 1 5 4 4 0 2x x x x x
22
4 1 5 4 6 0x x x x
2 10x
2 10x
22
( 4 5)( 4 3)x x x x m
241xx
( 4)( 4)
16 à 16
y y m
y m v y m
1 2 3 4
1 2 3 4 1 2 3 4
1 1 1 1 11
x x x x
x x x x x x x x
12
;xx
34
;xx
12
;xx
22
4 1 16 4 1 16 0x x m x x m
1 2 1 2
4 à . 1 16x x v x x m
34
;xx
22
4 1 16 4 1 16 0x x m x x m
3 4 3 4
4 à . 1 16x x v x x m
4 4 1 1 1
14
1 16 1 16 1 16 1 16
21
16 1 8 7
4
(1 16)( 1 16)
m m m m
mm
mm
22
22
2 4 2 21 3
2( 1) 3(7 )
x x y
xy
2
2( 1) 0x
27y
2
2( 1)x
2
7y
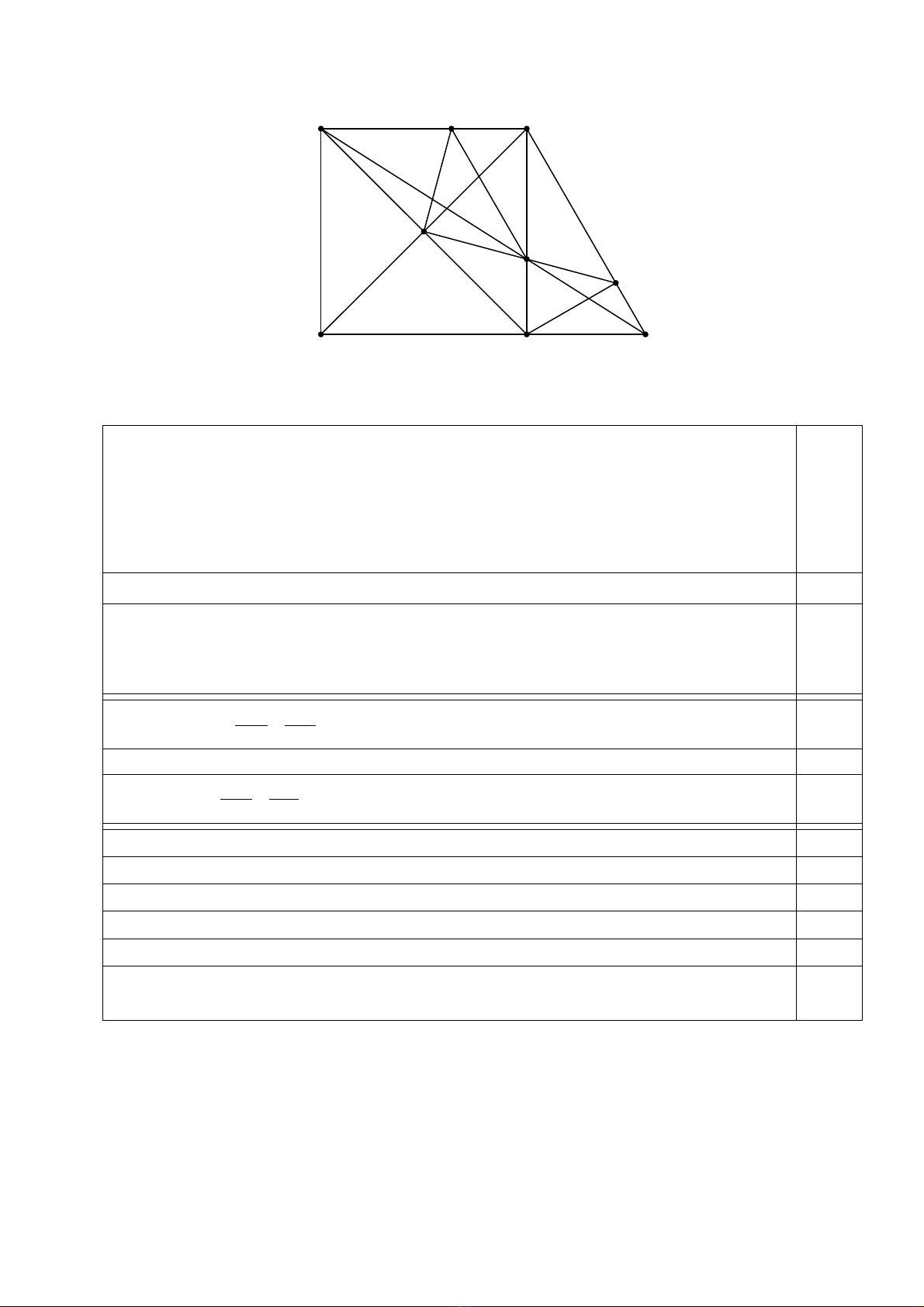
Bài 4 (7,0 điểm):
OBN và ∆OCM có:
BN = CM (gt)
OB = OC (ABCD là hình vuông)
OBN = OCM = 450.
∆OBN = ∆OCM
0,25
0,25
0,25
0,25
ON = OM (1)
0,25
Và BON = COM BON + BOM = COM + BOM
NOM =COB = 900 (2)
Từ (1) và (2) được ∆NOM vuông cân tại O.
0,50
0,50
0,25
AB // CE
AM BM
=
ME MC
(Theo Ta-Let)
0,75
Có BM = AN
NB = MC.
0,50
Thay được:
AM AN
=
ME NB
MN // BE (Theo Ta-Let đảo)
0,75
MN // BE BHM = NMO = 450 (1)
0,50
BMH = OMC (đối đỉnh) BMH đồng dạng với OMC
0,50
MH/MC = MB/MO
0,50
Và có HMC = OMB (đối đỉnh) MHC đồng dạng với MBO
0,50
MHC = MBO = 450 (2)
0,25
Từ (1) và (2) được BMC = BHM + MHC = 450 + 450 =900 .
Hay CH BE.
0,25
====HẾT====
H
E
N
O
D
C
A
B
M












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



