
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI TỈNH THPT
NĂM HỌC 2016-2017
ĐỀ THI CHÍNH THỨC
(Đề thi gồm có 01 trang)
Môn: Toán
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi thứ hai: 29/10/2016
Bài 5 (7,0 điểm).
1) Cho số tự nhiên n thỏa: 1 2
2 1 2 1 2 1
... 1023
n
n n n
C C C
. Tìm hệ số của số hạng
chứa x8 của khai triển (1 + x + x2
+ x3)n.
2) Tìm tất cả các cặp số nguyên tố
;
p q
thỏa mãn 2 2
5 4
p q
.
Bài 6 (7,0 điểm).
Cho tứ giác ABCD thỏa mãn
. . .
AB CD AD BC AC BD
. Biết rằng đường tròn
nội tiếp tứ giác ABCD có tiếp điểm với các cạnh AB, BC, CD và DA lần lượt tại K, L,
M và N.
1) Chứng minh rằng tứ giác ABCD nội tiếp được trong một đường tròn.
2) Chứng minh
2 2 2 2
KL MN KN LM
Bài 7 (6,0 điểm).
Tìm các số tự nhiên a1; a2; a3…; an thỏa mãn a1 + a2 + a3 + … + an = 2015
sao cho biểu thức P = a1.a2.a3…an lớn nhất có thể.
………………………… Hết ………………………….
Thí sinh không được sử dụng tài liệu và không được sử dụng máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh ………………………………..… Số báo danh ………… Phòng thi ……..
Cán bộ coi thi thứ nhất ……………………… Cán bộ coi thi thứ hai …………………………
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐĂK NÔNG
Vòng 2
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 12 THPT
NĂM HỌC 2016-2017
Môn: TOÁN
HƯỚNG DẪN CHẤM
(Hướng dẫn chấm gồm có 4 trang)
Lưu ý: Mọi cách giải khác đáp án, mà đúng và ngắn gọn đều cho điểm tương ứng.
Câu NỘI DUNG Điểm
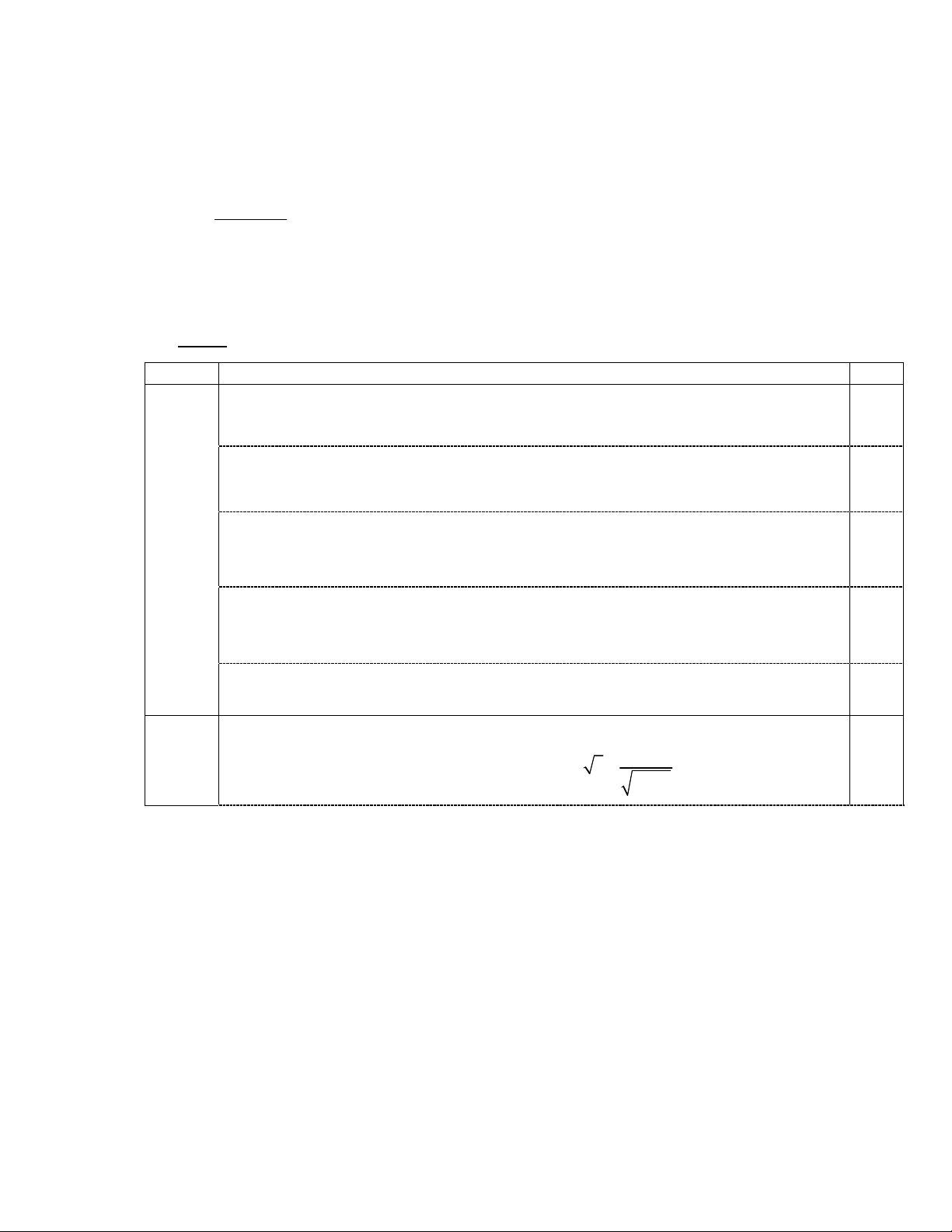
a. Cho số tự nhiên n thỏa: 1 2
2 1 2 1 2 1
... 1023
n
n n n
C C C
. Tìm hệ số của số
hạng chứa x8 của khai triển (1 + x + x2
+ x3)n. 2.0
2 1 2 1
2 1 2 1
2 1 2 1
0 0
(1 ) 2
n n
n k k n k
n n
k k
x C x C
0,5
Ta có:
2 1
2 1
2 1
0
2 2 2048 5
n
n k
n
k
C n
0,5
5 5
2 3 5 5 2 5 2
5 5
0 0
(1 ) (1 ) (1 ) .
k k m m
k m
x x x x x C x C x
0,5
1a.
2 điểm
Vì hệ số chứa x8 nên ta có k+2m =8 suy ra (k;m) = (0;4), (2;3), (4;2)
Vậy hệ số cần tìm là
0 4 2 3 4 2
5 5 5 5 5 5
. . . .
C C C C C C
0,5
1b.
5 điểm b. Cho dãy số thực
n
x
xác định bỡi
1
*
12
2015
3 ,
1
n
n
n
x
x
x n N
x
5, 0

2
1,0
1,0
1,0
1,0
1,0
2 7,0
a. Trong mặt phẳng với hệ tọa độ Oxy cho hai đường tròn
1 2
( ),( )
C C
lần lượt có
phương trình: 2 2
2 4 0
x y x y
; 2 2
2 6 1 0
x y x y
. Lập phương
trình đường thẳng d tiếp xúc với
1
( )
C
và cắt
2
( )
C
tại A, B thỏa mãn
2
1
arccos
9
AI B với I2 là tâm của đường tròn
2
( )
C
.
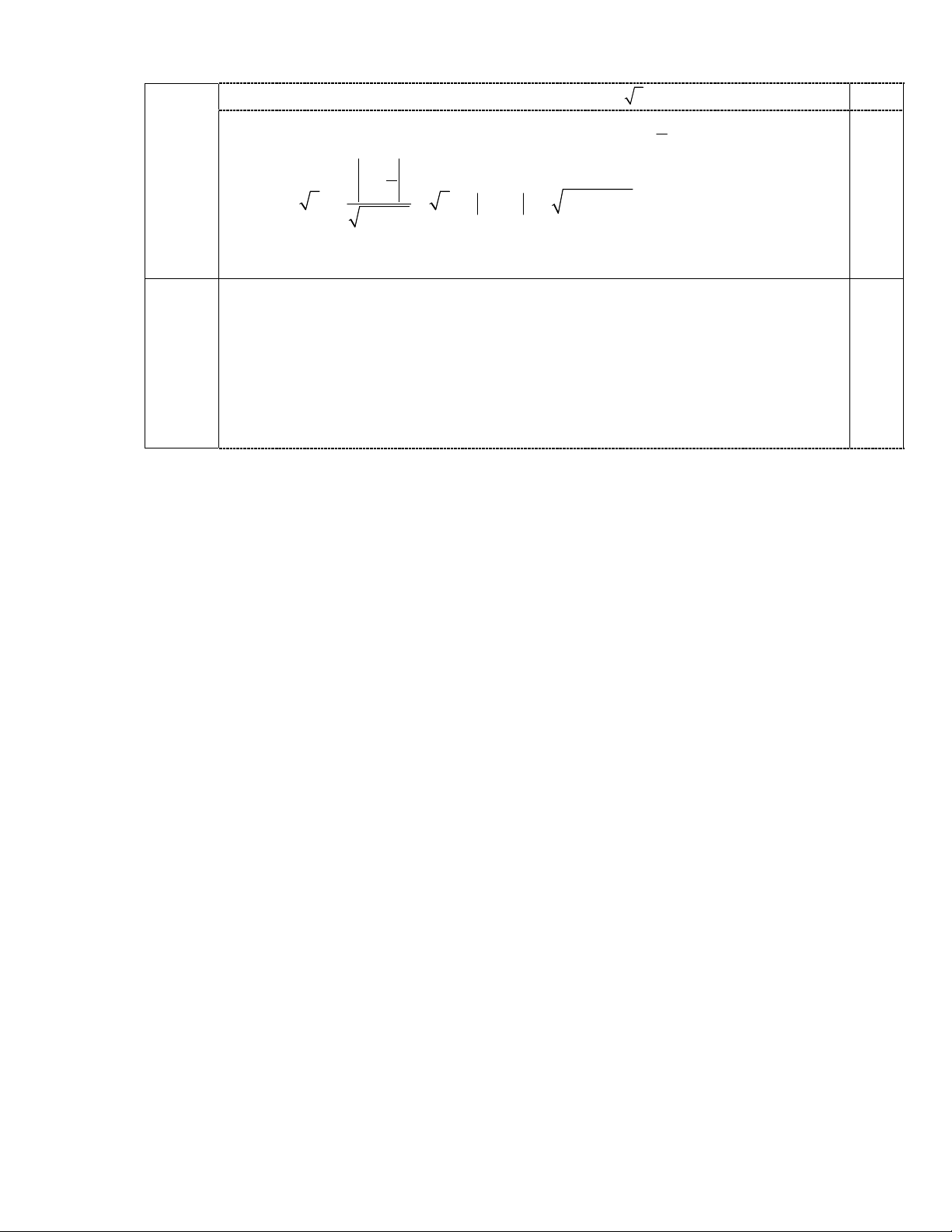
3.0
Ta có 1 1 2 2
(1; 2); R 5; ( 1; 3); R 3
I I
Phương trình đt I1I2 :
2 5 0
x y
. 0.75
Do
2
1
arccos
9
AI B nên
2
1
osAI
9
c B
Ta có:
2 2 2
2 2 2 2 2
2 . cos 16
AB I A I B I A I B AI B
suy ra 2 2
( ; ) 5
d I d I H .
H
B
A
I2
0.75
2a.
3.0
điểm
Do d tiếp xúc với
1
( )
C
nên 1 1
( ; ) 5
d I d R
Vì khoảng cách từ 2 điểm
1 2
;
I I
đến d bằng nhau nên d song song I1I2 hoặc d đi
qua trung điểm của I1I2. 1.0
3
Nếu d//I1I2 thì d có dạng:
2 0
x y m
; vì 1
( ; ) 5
d I d nên
0; 10
m m
Nếu d đi qua trung điểm của I1I2 thì d có dạng 5
( ) 0
2
ax b y
( 2 2
0
a b
)
2 2
12 2
2
( ; ) 5 5 2 2 5( )
b
a
d I d a b a b
a b
2 2 2 2
4 4 20 20
a ab b a b
2 2
19 4 16 0 0
a ab b a b
(vô lý)
ĐS:
2 0
x y
;
2 10 0
x y
0,5
2b.
4 điểm
b. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D,
AB = 2a, AD = DC = a. Góc giữa mặt phẳng (SBC) và mặt phẳng
(ABCD) bằng 600; I là t
rung điểm của AD, mặt phẳng (SIB) và mặt phẳng (SIC) cùng vuông góc
với mặt phẳng (ABCD), H là hình chiếu của I lên SD. Tính thể tích khối
chóp S.ABCD và khoảng cách từ H đến mặt phẳng (SBC) theo a.

4
1,0
1,0
1,0
1,0
Tìm các số tự nhiên a1; a2; a3…; an thỏa mãn a1 + a2 + a3 + … + an =
2015 sao cho biểu thức P = a1.a2.a3…an lớn nhất có thể. 6,0
Ta chứng tỏ trong các số a1; a2; a3…; an không có số 1.
Thật vậy, giả sử tồn tại một số bằng 1, chẳng hạn là a1 = 1, khi đó trong
các số còn lại phải có số aj >2, ta giả sử là a2 >2, vì ngược lại dễ thấy điều
vô lý.
1,5
3
6,0
điểm
Khi đó ta thay a1 bởi số 2 và a2 bỡi a2 -1
2
2 3
2
2 3 2 3
2 ( 1) ... 2015
2
2( 1) .. 1 . ...
n
n n
a a a a
a a a a a a
Vi phạm P = a1.a2.a3…an lớn nhất có thể.
1,0


























