UBND HUY N TAMỆ
D NGƯƠ
PHÒNG GD&ĐT
---------------
KÌ THI GIAO L U HSG GI I TOÁN Ư Ả
TRÊN MTCT L P 8 - NĂM H C 2014-2015Ớ Ọ
------------- ------------
Th i gian thi: ờ120 phút (không k th i gian giao đ)ể ờ ề
Chú ý: - Đ thi này có: 04 trangề
- Thí sinh làm bài tr c ti p vào b n đ thi này.ự ế ả ề
Đi m c a toàn bài thiể ủ
H và tên, ch kýọ ữ
các giám kh oả
S PHÁCH Ố
(Do Ch t ch HĐ ch m ghi )ủ ị ấ
B ng sằ ố B ng chằ ữ
......................................................
......................................................
Câu 1: (2 đi m) Choể các s th p phân vô h n tu n hoànố ậ ạ ầ :
E1 = 0,29972997... ; E2 = 0,029972997... ;E3 = 0,0029972997... v i chu k (2997)ớ ỳ
Ch ng minh r ng T = ứ ằ
1
3
E
+
2
3
E
+
3
3
E
là s t nhiên.ố ự
Tóm t t cách làm:ắK t qu :ế ả
T=
Câu 2: (2 đi m) ểTìm ch s th p phân th 13ữ ố ậ ứ 2011 sau d u ph y trong phép chiaấ ẩ
250000 cho 19.
Đáp số :
+ K t qu c a phép chia 250 000 cho 19 là:ế ả ủ
+ Ch s th p phân th 13ữ ố ậ ứ 2011 sau d u ph y trong phép chia 250000 cho 19ấ ẩ :
Câu 3: (2 đi m) ể Cho a = 546748605 và b = 437549310. Tìm CLN(a;b);Ư
BCNN(a,b).
1
ĐỀ CHÍNH THỨC
Đáp s :ố
CLN(a;b)Ư= ;BCNN(a,b)=
Câu 4: (2 đi m)ể
M t ng i l ng kh i đi m 2 000 000 đng/tháng, c sau 3 năm l i đcộ ườ ươ ở ể ồ ứ ạ ượ
tăng thêm 9,8%. H i sang năm th 10 l ng ng i đó là bao nhiêu đng/tháng?ỏ ứ ươ ườ ồ
Tóm t t cách gi iắ ả : K t qu :ế ả
(l y đn hàng đn v )ấ ế ơ ị
Câu 5: (4 đi m)ể
Cho đa th c ứ
9 7 5 3
1 1 13 82 32
( ) .
630 21 30 63 35
Q x x x x x x= − + − +
a/ Tìm s d khi chia đa th c ố ư ứ
( )Q x
cho
4x−
.
b/ Tính giá tr c a đa th c khi ị ủ ứ
4; 3; 2; 1;0x= − − − −
.
c/ Ch ng minh r ng đa th c ứ ằ ứ
( )Q x
nh n giá tr nguyên v i m i ậ ị ớ ọ
x
nguyên.
a/ Tóm t t cắách gi iả: K t qu :ế ả
b/ K t qu :ế ả
( 4)Q− =
;
( 3)Q− =
;
( 2)Q− =
;
( 1)Q− =
;
c/ Tóm t t cắách gi iả:
Câu 6: (3,5 đi m)ể
Cho dãy s ố
( ) ( )
5 7 5 7
2 7
n n
n
U+ − −
=
v i n = 0; 1; 2; 3; ...ớ
a/ Tính 5 s h ng đu tiên Uố ạ ầ 0, U1, U2, U3, U4
b/ L p công th c truy h i tính Uậ ứ ồ n + 2 theo Un+1 và Un .
c/ L p quy trình b m phím liên t c tính Uậ ấ ụ n + 2 theo Un + 1 và Un.
2
a/ K t quế ả :
U1 = U1 = U2 = U3 = U4 =
b/ Tóm t t cách gi iắ ả K t qu :ế ả
Câu 7: (2,5 đi m)ể
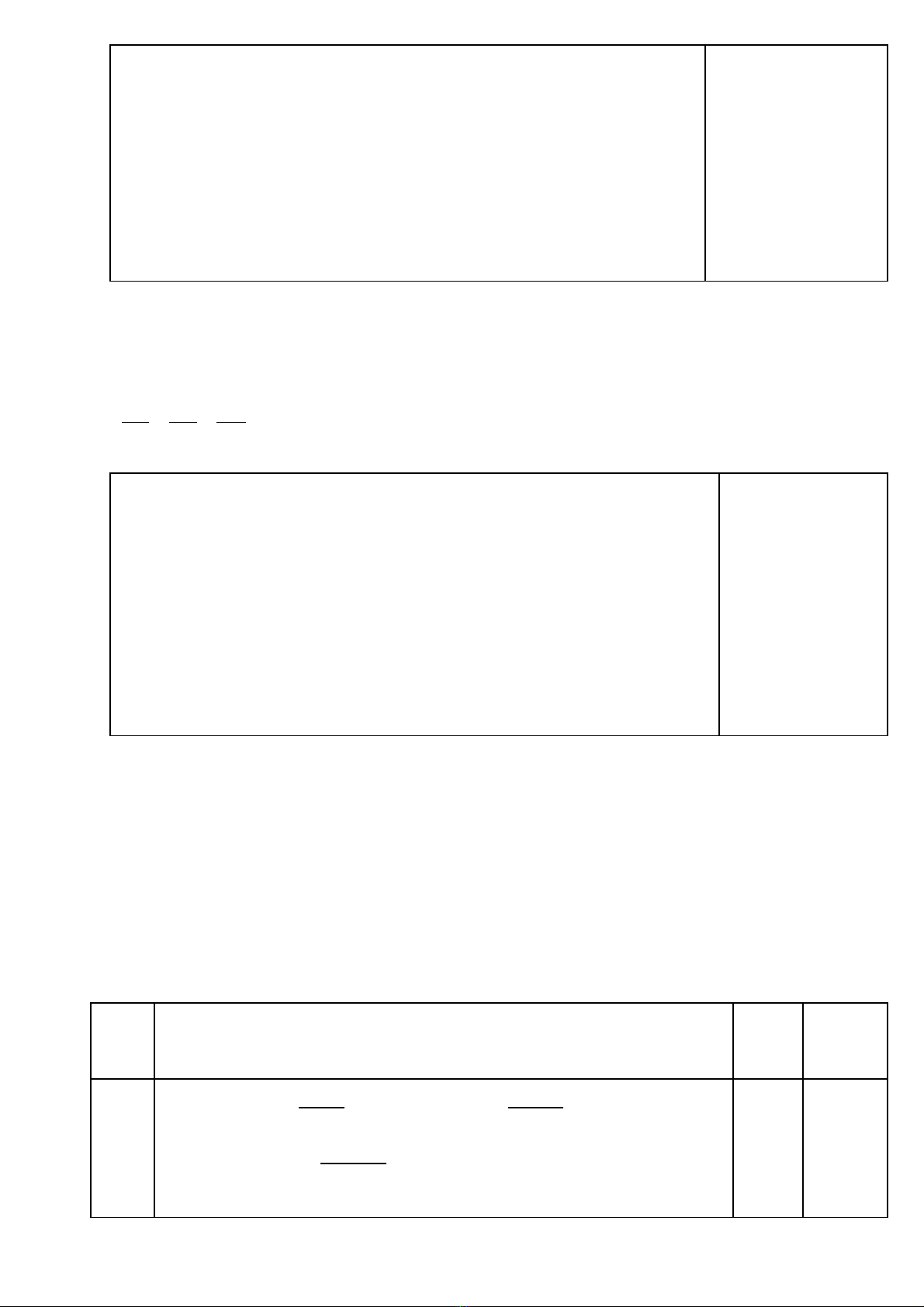
Cho tam giác ABC vuông t i A có AB = a = ạ4,6cm; AC = b = 6,2011cm. G i ọ
AM, AD l n l t là trung tuy n và phân giác trong c a tam giác (hình v ).ầ ượ ế ủ ẽ
a/ Tính đ dài đo n th ng BD. ộ ạ ẳ (K t qu l y v i 5 ch s th p phân)ế ả ấ ớ ữ ố ậ
b/ Tính di n tích tam giác ADM.ệ (K t qu l y v i 3 ch s th p phân)ế ả ấ ớ ữ ố ậ
a/ Tóm t t cắách gi iả: K t qu :ế ả
BD
3
c/ Qui tr×nh bÊm phÝm: (nói rõ trên lo i máy tính nào)ạ
B
A
C
MD
b/ Cách gi iảK t qu :ế ả
SADM=
Câu 8: (2,0 đi mể)
Cho h×nh thang ABCD cã hai ®êng chÐo AC vµ BD vu«ng gãc víi nhau t¹i
E, hai c¹nh ®¸y
3,56 ( ); 8,33( )AB cm DC cm= =
; c¹nh bªn
5,19 ( )AD cm=
. TÝnh gÇn
®óng ®é dµi c¹nh bªn BC vµ diÖn tÝch h×nh thang ABCD. Cho biÕt
EA EB AB
EC ED DC
= =
.
(K tế qu lảàm tròn đn ch s th p phân th 5)ế ữ ố ậ ứ
Tóm t t cách gi i:ắ ả K t qu :ế ả
BC=
SABCD=
--H t—ế
UBND HUY N TAMỆ
D NGƯƠ
PHÒNG GD&ĐT
----------------
KÌ THI GIAO L U HSG GI I TOÁN Ư Ả
TRÊN MTCT L P 8Ớ
------------- --
ĐÁP ÁN VÀ THANG ĐI MỂ
Câu Tóm t t cách gi i và k t quắ ả ế ả §iÓ
m
TP
§iÓm
toµn
bµi
1E1 = 0,(2997)
2997
9999
=
; E2 = 0,0(2997)
2997
99990
=
E3 = 0,00(2997)
2997
999900
=
Thay E1, E2, E3 vào bi u th c Tể ứ đc k t qu :ượ ế ả
1
2
4
T=1111 1
2
Ta có 17 : 19 = 13157,(894736842105263157).Chu k g m 18 ỳ ồ
ch s .ữ ố
Ta có
( )
670
3 2011 3
13 1(mod18) 13 13 .13 13(mod18)
=
Suy ra s c n tìm đng v trí th 13 trong chu k 18 ch s ố ầ ứ ở ị ứ ỳ ữ ố
th p phân.ậ
Đáp s : S 2. ố ố
1
1
2
3
CLN(a;b)Ư= 45
BCNN(a,b)= 5316210552471390
1
12
4
G i s ti n l ng kh i đi m là a (đng), sau 3 năm tăng mọ ố ề ươ ở ể ồ
(%).Trong 3 năm đu l ng c a ng i đó là: a (đng)ầ ươ ủ ườ ồ
Trong các năm th 4, 5 và 6 l ng c a ng i đó là: a+a.mứ ươ ủ ườ
(đng)ồ
Trong các năm th 7, 8 và 9 l ng c a ng i đó là:ứ ươ ủ ườ
a+a.m +(a+a.m )m=
2
(1 )a m+
(đng)ồ
Năm th 10 l ng c a ng i đó là:ứ ươ ủ ườ
3
(1 )a m+
(đng)ồ
Thay a=2 000 000; m=9,8% ta tính đc l ng c a ng i đóượ ươ ủ ườ
Đáp s : 2 647506 đng.ố ồ
1
1
2
5
a/ S d trong phép chia ố ư
( )Q x
cho
4x−
chính b ng ằ
( )
4Q
( )
4Q
=0
0,5
1
4
b/ Khi
4; 3; 2; 1;0x= − − − −
thì
( )
Q x
=0 1
c/ Ta th y t i ấ ạ
4; 3; 2; 1;0;1;2;3;4x= − − − −
thì
( )
Q x
=0 nên
1
( ) ( 4)( 3)( 2)( 1) ( 1)( 2)( 3)( 4)
630
Q x x x x x x x x x x= + + + + − − − −
Mà trong 9 s nguyên liên ti p luôn có s chia h t cho 2; 5; 7; ố ế ố ế
9
v i m i ớ ọ
x
nguyên
( 4)( 3)( 2)( 1) ( 1)( 2)( 3)( 4)x x x x x x x x x+ + + + − − − −
chia h t cho ế
(2.5.7.9) 630=
( )Q x
nh n giá tr nguyênậ ị
.x Z∀
0,75
0,75
U0=0; U1=1; U2=10; U3=82; U4=640. 1
5