ĐỀ THI HSG NĂM 2011- 2012
Môn Thi : Toán 11
Thời gian làm bài : 180 phút
Câu I( 1 điểm): Giải phương trình
(sin 2 sin 4) cos 2
0
2sin 3
x x x
x
Câu II(2 điểm):
1/ Từ các chữ số 1;2;3;4;5;6 có thể lập được bao nhiêu số tự nhiên có 3 chữ số
đôi một khác nhau sao cho mỗi số đó chia hết cho 3.
2/ Tìm số nguyên dương n sao cho:
1 2 3 2 1
2 2
2 1 2 1 2 1 2 1
2.2 3.2 ... (2 1).2 2011
n
n
n n n n
n
C C C C
Câu III(2 điểm) : Cho hàm số: 3 2
3 2
y x x
(C)
1/ Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến song song với
đường thẳng
9 2011
y x
.
2/ Tìm tất cả các điểm thuộc đồ thị (C ) mà qua đó kẻ được một và chỉ một tiếp
tuyến với đồ thị ( C ).
Câu IV(2 điểm):
1/ Chứng minh phương trình :
4 3 2
2 2011 0
x mx nx px
có ít nhất 2 nghiệm với
m,n,p
R
2/ Tính :
2
1
3 2011 2009
1
x
x x
Lim
x
Câu V( 3 điểm) : Cho hình chóp S.ABCD đáy là hình thoi tâm O, cạnh a, góc
BAD=600 ; SO vuông góc với mặt phẳng (ABCD);
3
4
a
SO . Gọi E là trung
điểm của AD, F là trung điểm của DE.
1/ Chứng minh (SOF)
(SAD).
2/ Tính khoảng cách từ O và C đến mặt phẳng (SAD).
3/ Gọi
là mặt phẳng qua BC và vuông góc với mặt phẳng (SAD). Xác định
thiết diện của hình chóp với mặt phẳng
. Tính diện tích của thiết diện này.
.........................Hết…………….
Đáp án đề thi HSG môn toán lớp 11 lần 2 (2010-2011)
Câu Nội dung Điểm
I Xét phương trình: ( 2 sin 4)cos 2
0
2sin 3
Sin x x x
x
(1)
Điều kiện:
3
sin
2
x
Phương trình (1)
sin2x.cosx-
1
2
sin2x+4cosx-2=0
sin2x(cosx-
1
2
)+4(cosx-
1
2
)=0
(cosx-
1
2
)(sin2x+4)=0
x=
2
3
k
Đối chiếu với điều kiện: x=
2
3
k
Vậy phương trình có nghiệm: x=
2
3
k
0,25
0,5
0,25
II
1
.Đặt A= {1;2;3;4;5;6}
.Các tập hợp con của A gồm có 3 phần tử và tổng của các phần
tử đó chia hết cho 3 là:
{1;2;3}, {1;2;6}, {2;3;4}, {1;3;5}, {1;5;6},{2;4;6}, {3;4;5},
{4;5;6}.
0,5
Có 8 tập
Ứng với mỗi tập hợp trên ta có thể lập được
3=3.2.1=6 (số) thỏa mãn yêu cầu bài toán
Vậy có 8.6=48 số cần tìm
0,5
2 Ta có
2 1 0 1 2 2 3 3 2 1 2 1
2 1 2 1 2 1 2 1 2 1
(1 ) . . . .... .
n n n
n n n n n
x c c x c x c x c x
(1) 0,25
Lấy đạo hàm cả hai vế của (1) theo x ta được
2 1 2 3 2 2 1 2
2 1 2 1 2 1 2 1
(2 1)(1 ) ( 1) 2 . 3. . .... (2 1). .
n n n
n n n n
n x c c x c x n c x
2 1 2 3 2 2 1 2
2 1 2 1 2 1 2 1
(2 1)(1 ) 2 . 3. . .... (2 1). .
n n n
n n n n
n x c c x c x n c x
(2)
0,5
Cho x=2 vào hai vế của (2) ta được:
1 2 1 2
2 1 2 1
2 1 ...... (2 1). .2
n n
n n
n c n c
Khi đó: 2n+1=2011
n=1005.
Vậy n=1005.
0,25
Đường thẳng
song song với đường thẳng y=-9x+2011 có
phương trình dạng y= -9x+m (m
2011)
0,25
Đường thẳng
là tiếp tuyến của (c )
hệ phương trình
3 2
2
3 2 9
3 6 9
x x x m
x x
có nghiệm
0,25
Giải (2):
1
3
x
x
Nếu x=-1 thì thế vào phương trình (1) ta được m=-7 (thỏa mãn).
phương trình tiếp tuyến: y=-9x-7.
Nếu x=3 thì m=25( thỏa mãn)
phương trình tiếp tuyến: y= -9x+25
Vậy có 2 phương trình tiếp tuyến:y=-9x-7,y= -9x+25.
0,5
2 Goi M(x0,f(x0)
(c ); f(x0)= 3 2
0 0
3 2
x x
.
Đường thẳng
với hệ số góc k đi qua điểm M(x0,f(x0) có
phương trình là: y= k(x-x
0
)+ f(x
0
)
0,25
là tiếp tuyến của (c )
hệ phương trình
3 2
0 0
2
3 2 ( ) ( )
3 6 1
x x k x x f x
x x
có nghiệm
0,25
(x-x
0
)[-2x
2
+(x
0
+3)x+x
0
2
-3x
0
]=0
0
2 2
0 0 0
( ) 2 ( 3) 3 0
x x
g x x x x x x
= (x0+3)2+8(x0
2-3x0)=9x0
2-18x0+9=9(x0-1)2>0
Yêu cầu bài toán
g(x)=0 có nghiệm kép x=x0
0
0
0
3
4
x
x
x0=1
M(1;0)
Vậy M(1;0)
0,5
IV
1
Xét phương trình: 4 3 2
2 2011 0
x mx nx px
(1)
Xét hàm số: 4 3 2
( ) 2 2011
f x x mx nx px
4 3 2
lim ( ) lim ( 2 2011)
x x
f x x mx nx px
 

b>0 sao cho f(b) <o
4 3 2
lim ( ) lim ( 2 2011)
x x
f x x mx nx px
 
a<0 sao cho f(a) <o
0,5
f(0)=2011>0
Hàm số f(x) liên tục trên các đoạn [a;0] và [o;b];
( ). (0) 0
(0). ( ) 0
f a f
f f b
phương trình có ít nhất 1 nghiệm x1
(a;0) và ít nhất 1
nghiệm x2
(0;b).
Vậy phương trình có ít nhất 2 nghiệm.
0,5
2
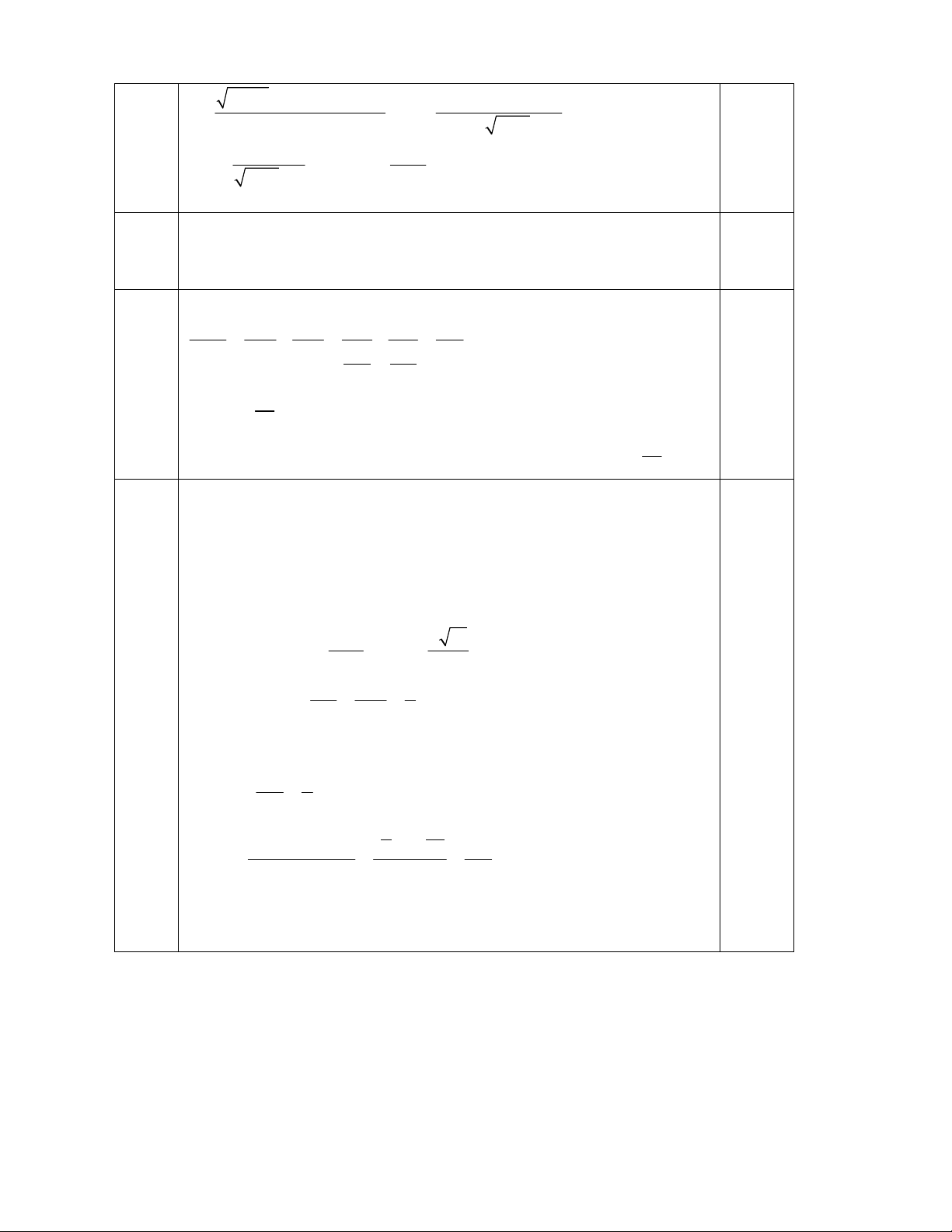
2 2
1 1
1
3 2 2011( 1) 3 4
lim lim[ 2011]
1( 1)( 3 2)
1 4021
lim( 2011) 2
3 2
x x
x
x x x
xx x
x
x
V
1
Tam giác ABD đều nên
BE AD
; OF//BE OF
AD
(1)
( )
SO ABCD SO AD
(2)
Từ (1) và (2)
( OF) ( ) ( OF)
AD S SAD S
1,0
2 Kẻ
OH SF
tại H
( )
OH SAD
( ;( ))
d O SAD OH
2 2
2 2 2 2
1 1 1 1 1 64
9 3
OF 9
16 16
3
8
a a
OH SO a
a
OH
O là trung điểm của AC nên
3
( ;( )) 2 ( ; ( ))
4
a
d C SAD d O SAD
0,25
0,5
0.25
3 Gọi K là hình chiếu của C trên mp(SAD)
H là trung điểm
của AK
( ) ( )
mp mp BCK
;BC//AD nên mp(BCK) cắt mp(SAD) theo
giao tuyến song song với AD.Từ K kẻ đường thẳng song song
với AD cắt SD, SA tại M và N .Thiết diện tạo thành là hình
thang BCMN
2
2 2 2
2
2
2
12 12
OF
16 4
3
.4
a a
SF SO SF
SH SO
SO SH SF SF SF
MN cắt SF tại trung điểm I
MN là đường trung bình của
tam giác SAD
2
2 2
3
( )
( ) 9
2 4
2 2 16
td
AD a
MN
a a
a
MN BC CK a
S