S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
QU NG NAMẢK THI OLYMPIC 24/3 T NH QU NG NAMỲ Ỉ Ả
NĂM 2021
Môn thi : TOÁN 10
Th i gian:ờ 150 phút (không k th i gian giao đ)ể ờ ề
Ngày thi : 20/03/2021
Câu 1 (5,0 đi m).ể
a) Gi i ảph ng trìnhươ
b) Gi iả h ph ng trình ệ ươ
Câu 2 (4,0 đi m). ể
a) Cho hàm s có đ th (ố ồ ị C).
Tìm t t c các đi m trên đ th (ấ ả ể ồ ị C) có tung đ b ng ộ ằ
b) Cho parabol : . Tìm các h s đ đi qua và c t tr c hoành t i hai đi m sao cho tamệ ố ể ắ ụ ạ ể
giác đu, v i là đnh c a ề ớ ỉ ủ
Câu 3 (4,0 đi m).ể
a) Tìm giá tr nh nh t c a hàm s trên n a kho ng ị ỏ ấ ủ ố ử ả
b) Cho hai s th c d ng th a mãn ố ự ươ ỏ
Tìm giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
Câu 4 (3,0 đi m). ể
a) Cho hình vuông là trung đi m c a n m trên c nh sao cho là trung đi m c a ể ủ ằ ạ ể ủ Hai
đi m l n l t là tr ng tâm c a hai tam giác ể ầ ượ ọ ủ
Hãy bi u th vect theo hai vect ể ị ơ ơ và ch ng minh ứ vuông góc v i ớ
b) Cho tam giác có Đi m ển m trên c nh sao cho Tính đ dài các đo n th ng ằ ạ ộ ạ ẳ
Câu 5 (4,0 đi m). ể
a) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, cho đi m và đng th ng (ể ườ ẳ d) có ph ngươ
trình . Vi t ph ng trình đng tròn (ế ươ ườ C) đi qua A và ti p xúc v i đng th ng (ế ớ ườ ẳ d) t i ạ
b) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, cho tam giác vuông cân t i ạB. Các đi mể M, N
l n l tầ ượ là trung đi m c a ể ủ AB, AC và là tr ng tâm c a tam giác Đi m ọ ủ ể E thu c c nh ộ ạ AC
sao cho ( khác ) và đng th ng ườ ẳ có ph ng trình . Đi m ươ ể M thu c đng th ng , ộ ườ ẳ B thu cộ
đng th ng và ườ ẳ A có hoành đ l n h n Tìm t a đ các đi m ộ ớ ơ ọ ộ ể A, B, C.
–––––––––––– H t ––––––––––––ế
Thí sinh không đc s d ng tài li u. Cán b coi thi không gi i thích gì thêm.ượ ử ụ ệ ộ ả
H và tên thí sinh: …..…………ọ……………….………. S báo danh: …ố…….………
S GIÁO D C VÀ ĐÀOỞ Ụ
T OẠ
QU NG NAMẢ
K THI OLYMPIC 24/3 T NH QU NG NAM Ỳ Ỉ Ả
NĂM 2021
ĐÁP ÁN – THANG ĐI MỂ
Môn thi: TOÁN 10
(Đáp án – Thang đi m g m 06 trangể ồ )
CâuĐáp ánĐiể
m
Câu
1
(5,0
đi mể
)
a) Gi i ảph ng trìnhươ 2,5
Đi u ki n:ề ệ
Đt ặ
Ph ng trình (2) tr thành: ươ ở
(th a).ỏ
b) Gi iả h ph ng trình ệ ươ 2,5
Đi u ki n ề ệ
Khi đó pt th hai vi t l i: ứ ế ạ
Suy ra đc nghi m c a h : (5ượ ệ ủ ệ ; 20).
Câu 2
(4,0
đi m)ể
a) Cho hàm s có đ th (C). ố ồ ị
Tìm t t c các đi m trên đ th (C) có tung đ b ng ấ ả ể ồ ị ộ ằ 2,0
thuvienhoclieu.com Trang 2
V y có hai đi m th a đ ậ ể ỏ ề
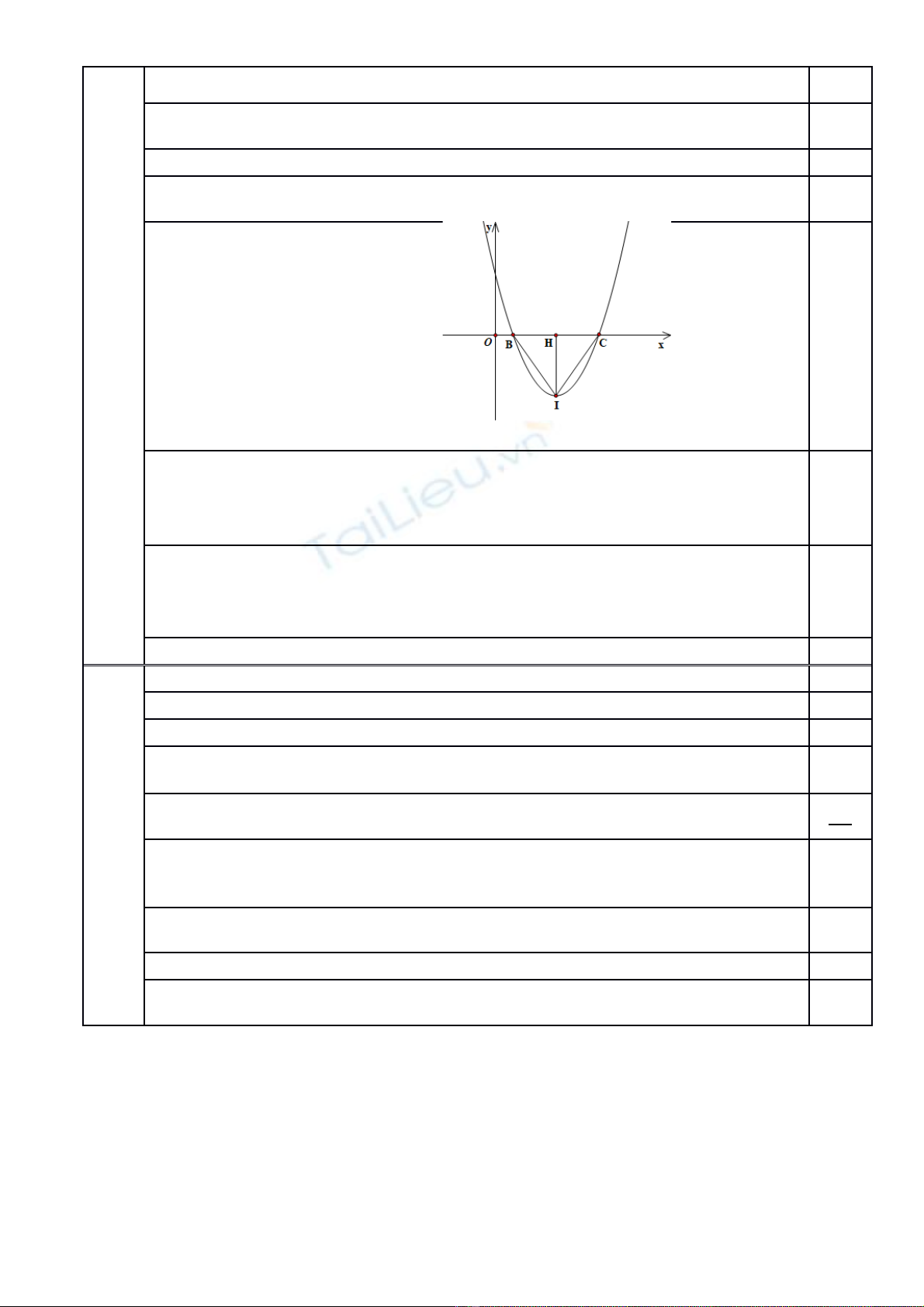
b) Cho parabol :. Tìm các h s đ đi qua và c t tr c hoành t i hai đi m sao cho tam ệ ố ể ắ ụ ạ ể
giác đu, v i là đnh c a ề ớ ỉ ủ 2,0
Parabol đi qua nên (1)
Ph ng trình hoành đ giao đi m c a ươ ộ ể ủ (P) và tr c hoành là ụ(*)
(P) c t tr c hoành t i hai đi m phân bi t ắ ụ ạ ể ệ B, C
Ph ng trình (*) có hai nghi m phân bi t ươ ệ ệ
Parabol (P) có đnh ỉ
Gi s :ả ử ; trong đó là hai nghi m c a pt (*)ệ ủ
Tam giác IBC đu khi ề
(2)
T (1) và (2) ta có hừ ệ : ho c .ặ
Câu 3
(4,0
đi m)ể
a) Tìm giá tr nh nh t c a hàm s trên n a kho ng ị ỏ ấ ủ ố ử ả 1,5
D u “ = ” x y ra khi ấ ả
V y giáậ tr nh nh t c a hàm s trên nị ỏ ấ ủ ố ửa kho ngả là
b) Cho hai s th c d ng th a mãn ố ự ươ ỏ
Tìm giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ 2.5
Đt , ta có: ặ
.
Suy ra (d u “=” x y ra khi ).ấ ả
(b t đng th c Côsi) ấ ẳ ứ
(b t đng th c v i )ấ ẳ ứ ớ
Suy ra: , . V y khi .ậ
thuvienhoclieu.com Trang 3
Câu 4
(3,0
đi m)ể
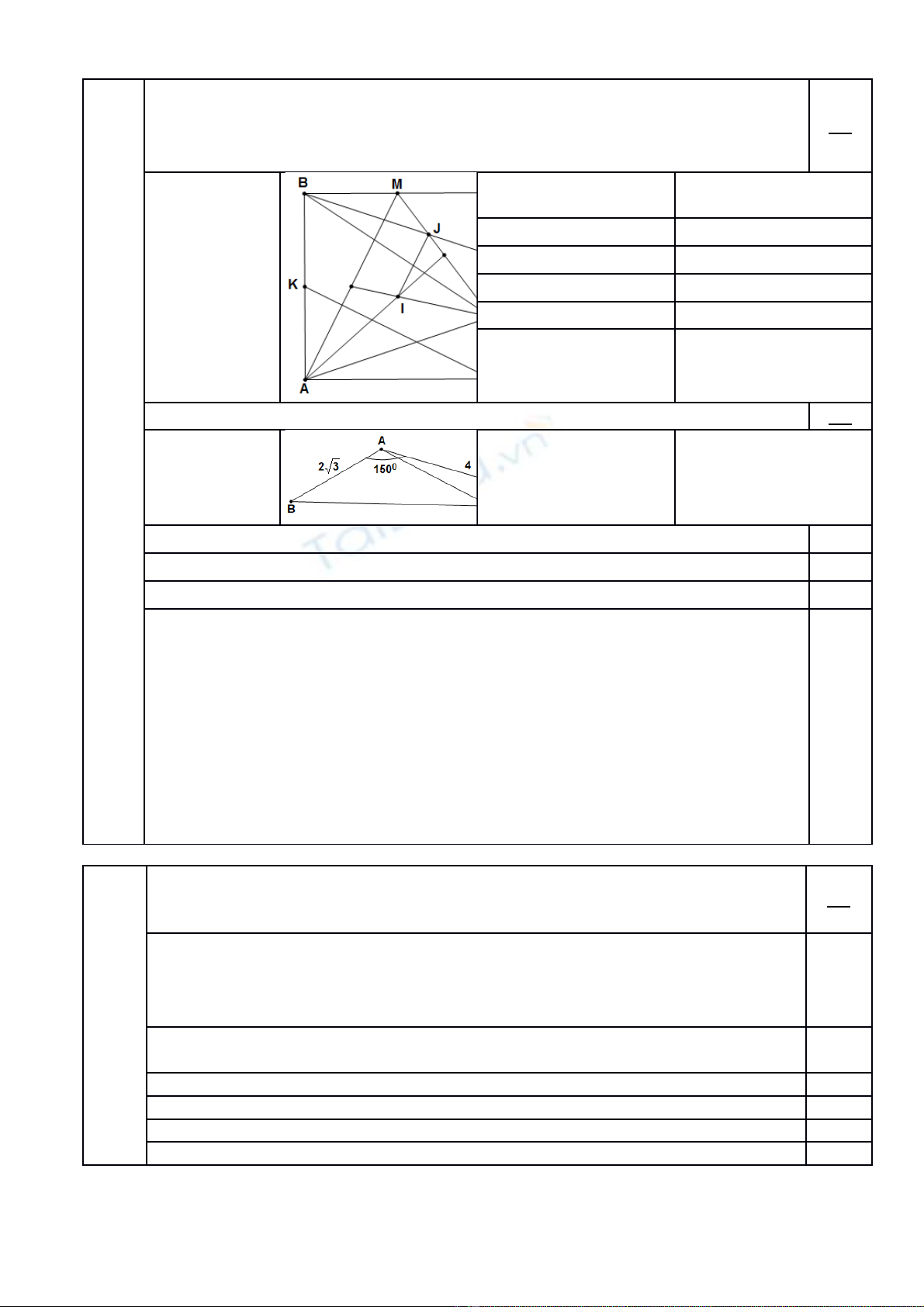
a) Cho hình vuông có c nh b ng là trung đi m c a n m trên c nh sao cho là trungạ ằ ể ủ ằ ạ
đi m c a ể ủ Hai đi m l n l t là tr ng tâm c a hai tam giác ể ầ ượ ọ ủ Hãy bi u th theo haiể ị
vect ơ ch ng minh ứ vuông góc v i ớ1,5
Suy ra vuông góc v i ớ
b) Cho tam giác có Đi m ển m trên c nh sao cho Tính ằ ạ 1,5
Cách khác :
Câu 5
(4,0
đi m)ể
a) Trong m t ph ng v i h t a đ Oxy, cho đi m và đng th ng (d) có ph ngặ ẳ ớ ệ ọ ộ ể ườ ẳ ươ
trình . Vi t ph ng trìnhế ươ đng tròn (C) đi qua A và ti p xúc v i đng th ng (d)ườ ế ớ ườ ẳ
t i ạ1,5
+ G i ọ là tâm c a đng tròn ủ ườ (C).
+ (d) có m t vect ch ph ng là ộ ơ ỉ ươ
+ Đng tròn (C) ti p xúc v i đng th ng (d) t i nên ườ ế ớ ườ ẳ ạ
+ Đng tròn (C) đi qua A(ườ 3;1) nên
T (1) và (2) suy ra. Suy raừ
Bán kính c a đng tròn là ủ ườ
Suy ph ng trình đng tròn (ươ ườ C):
thuvienhoclieu.com Trang 4
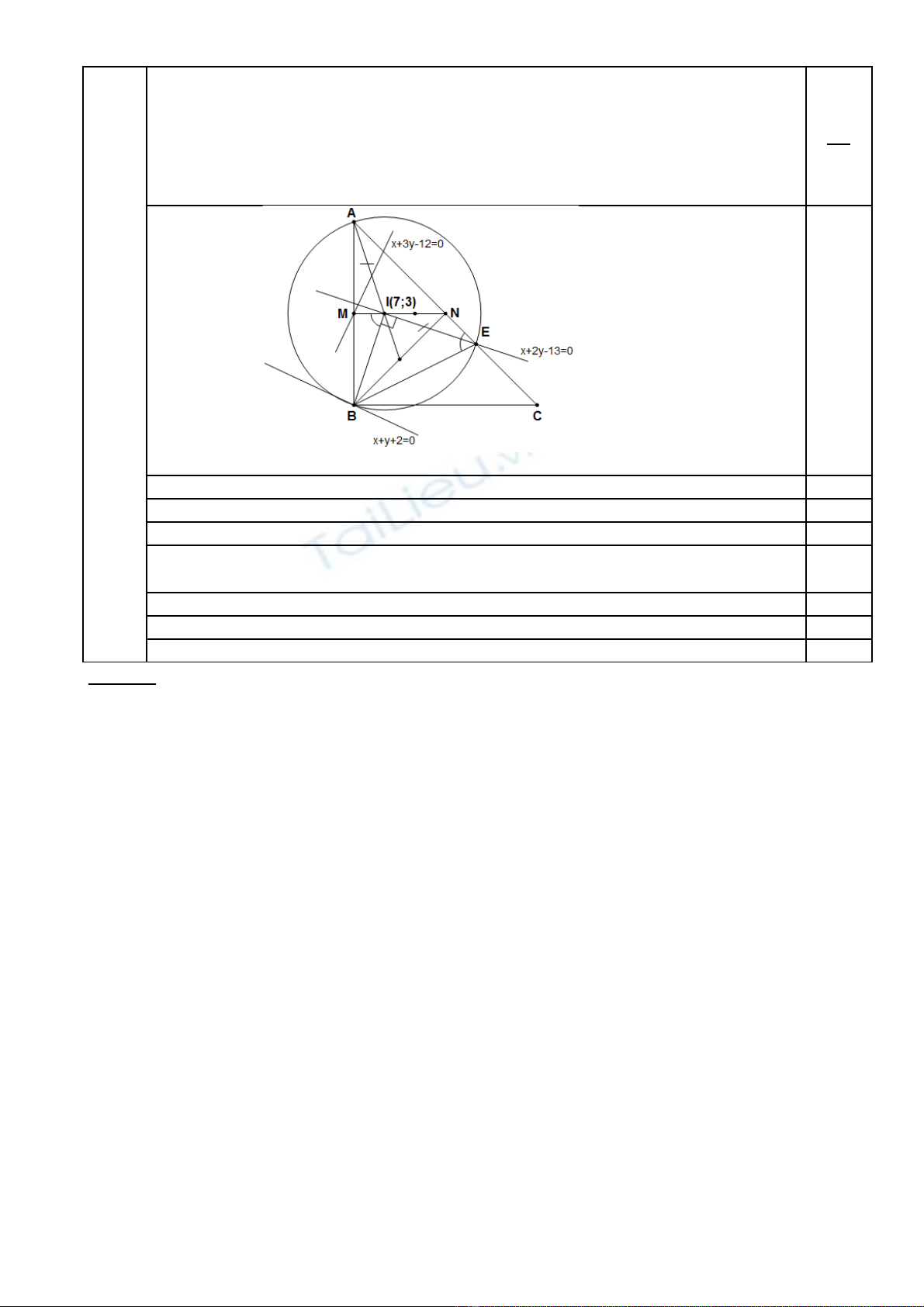
b) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, cho tam giác vuông cân t i ạB. Các đi mể
M,N l n l tầ ượ là trung đi m c a ể ủ AB, AC và là tr ng tâm c a tam giác Đi m ọ ủ ể E
thu c c nh ộ ạ AC sao cho ( khác ) và đng th ng ườ ẳ có ph ng trình . Đi m ươ ể M thu cộ
đng th ng , ườ ẳ B thu c đng th ng và ộ ườ ẳ A có hoành đ l n h n Tìm t a đ cácộ ớ ơ ọ ộ
đi m ểA, B, C.
2,5
(HV: 0,25 đi m)ể
Ch ng minh đc t giác ứ ượ ứ BINE n i ti p và suy ra .ộ ế
Vi t đc ph ng trình đng th ng ế ượ ươ ườ ẳ BI là
M t khác B thu c ,suy ra ặ ộ
M thu c ộ
. V y ậ
Suy ra ptđt AC là
Ghi chú:
Trong nh ng ý ch a phân rã ra 0,25đ thì n u c n Ban Giám kh o có th th ng nh t rã raữ ư ế ầ ả ể ố ấ
chi ti t 0,25đ, nh ng l u ý t ng đi m c ý đó v n không điế ư ư ổ ể ả ẫ ổ ;
N u h c sinh có cách gi i khác đúng, chính xác và logic thì Ban Giám kh o th o lu n vàế ọ ả ả ả ậ
th ng nh t thang đi m cho đi m phù h p v i H ng d n ch m.ố ấ ể ể ợ ớ ướ ẫ ấ
thuvienhoclieu.com Trang 5