S Giáo d c & Đào t o TP Đàở ụ ạ
N ngẵ
Tr ng THPT Thái Phiênườ
Đ THI TH ĐI H C - CAO ĐNGỀ Ử Ạ Ọ Ẳ
NĂM H C 2008 - 2009 L N IỌ Ầ
MÔN TOÁN, KH I DỐ
(Th i gian 180 phút, không k th i gian giao đ)ờ ể ờ ề
Câu 1: (2 đi m) ể
1) Kh o sát s bi n thiên và v đ th (C) c a hàm s ả ự ế ẽ ồ ị ủ ố
4 2
1 3
y x x
4 2
= −
.
2) D a vào đ th (C), tìm các giá tr c a tham s m đ ph ng trình sau có 4ự ồ ị ị ủ ố ể ươ
nghi m phân bi t ệ ệ
4 2 2
1x 3x 2m 4 0
2− − + =
.
Câu 2: (2 đi m)ể
1) Gi i ph ng trình (sinx + cosx)ả ươ 2 -
3
cos2x = 1.
2) Gi i h ph ng trình ả ệ ươ
3 3
xy(x y) 2 (x, y )
x y 7
− =
− =
ﾡ
.
Câu 3: (2 đi m)ể
1) Tìm giá tr l n nh t và nh nh t c a hàm s : ị ớ ấ ỏ ấ ủ ố
2
y x 1 x= −
.
2) Cho hai đng th ng song song dườ ẳ 1, d2. Trên d1 l y 15 đi m phân bi t, trên dấ ể ệ 2
l y 18 đi m phân bi t. Tính s tam giác có các đnh là 3 đi m trong s 33ấ ể ệ ố ỉ ể ố
đi m đã ch n trên dể ọ 1 và d2.
Câu 4: (2 đi m)ể
1) Trong m t ph ng t a đ Oxy cho tam giác ABC có đnh A(1;0) và hai đngặ ẳ ọ ộ ỉ ườ
th ng l n l t ch a các đng cao v t B và C có ph ng trình t ng ng làẳ ầ ượ ứ ườ ẽ ừ ươ ươ ứ
x - 2y + 1 = 0 và 3x + y - 1 = 0. Tính di n tích tam giác ABC.ệ
2) Cho hình chóp t giác S.ABCD có đáy là hình thang ABCD vuông t i A vàứ ạ
D, bi t AB = AD = a, CD = 2a. C nh bên SD vuông góc v i m t ph ngế ạ ớ ặ ẳ
(ABCD), SD = a. Tính th tích kh i chóp S.ABC và kho ng cách t đi m Aể ố ả ừ ể
đn m t ph ng (SBC).ế ặ ẳ
Câu 5: (2 đi m)ể
1) Gi i ph ng trình: logả ươ 4(x + 2) = log2x.
2) Gi i b t ph ng trình: 5ả ấ ươ x + 12x > 13x.
-----H TẾ-----
Thí sinh không đc s d ng tài li u. Giám th không gi i thích gì thêmượ ử ụ ệ ị ả
1
H và tên thí sinhọ: ………………………… S báo danhố: ………………………………
S Giáo d c & Đào t o TP Đàở ụ ạ
N ngẵ
Tr ng THPT Thái Phiênườ
ĐÁP ÁN THI TH ĐI H C - CAO ĐNGỬ Ạ Ọ Ẳ
NĂM H C 2008 - 2009 L N IỌ Ầ
MÔN TOÁN, KH I DỐ
CâuĐáp ánĐiể
m
1
1) + T p xác đnh D = ậ ị
ﾡ
.
+ S bi n thiên y’ = xự ế 3 - 3x = x(x2 - 3)
y’ = 0
x(x2 - 3) = 0
x 0 y 0
9
x 3 y 4
= =�
= = −��
B ng bi n thiên đy đ các vô c c, CĐ, CTả ế ầ ủ ự
+ Đ th : Dáng đi u đúng và đi qua các đi m ồ ị ệ ể
( )
0;0 ;
( )
9
3; ; 6;0
4
� �
−
� �
� �
0,25
0,25
0,25
0,25
2) + Ph ng trình ươ
4 2 2
1 3
x x m 2
4 2
− = −�
+ S nghi m c a ph ng trình b ng s giao đi m c a đ th (C)ố ệ ủ ươ ằ ố ể ủ ồ ị
và đng th ng (d): y = mườ ẳ 2 - 2.
+ ycbt
2
9m 2 0
4
− < − <
.
+ K t qu : ế ả
2 m 2− < <
.
0,25
0,25
0,25
0,25
2
1) Ph ng trình ươ
sin2x -
3
cos2x = 0.
sin 2x 0
3
2x k
3
x k (k )
6 2
π
� �
− =�� �
� �
π
− = π�
π π
= +� �ﾡ
0,25
0,25
0,25
0,25
2) +
3 3
xy(x y) 2 (1)
x y 7 (2)
− =
− =
T (1) và (2) ừ
2(x3 - y3) = 7xy(x - y)
(x - y)(2x2 - 5xy + 2y2) = 0
2x2 - 5xy + 2y2 = 0 (3) (do (1)
x - y ≠ 0)
0,25
0,25
2
Coi (3) là ph ng trình n x ươ ẩ
x = 2y v
y
x2
=
+ V i x = 2y ớ
3
x 2y x 2
y 1
7y 7
==
� �
� � =
=
V i x = ớ
3
y 2x x 1
y
y 2
2x 1
== −
� �
� � = −
= −
+ Th l i và k t lu n h có 2 nghi m (x;y) = (2;1) và (x;y) = (-1;-ử ạ ế ậ ệ ệ
2)
0,25
0,25
3
1) + T p xác đnh: D = [-1;1]ậ ị
2 2
2
2 2
x 1 2x
y' 1 x
1 x 1 x
−
= − − =
− −
+ y’ = 0
1 - 2x2 = 0
1
x ( 1;1)
2
= −� � �
+ y = f(x) = x
2
1 x−
nên f(-1) = 0, f(1) = 0,
1 1
f ,
2
2
� �
− = −
� �
� �
1 1
f2
2
� �
=
� �
� �
.
+
[ ] [ ]
1;1 1;1
1 1
Maxy , Miny
2 2
− −
= = −
.
0,25
0,25
0,25
0,25
2) + S đo n th ng t o nên t 15 đi m phân bi t trên dố ạ ẳ ạ ừ ể ệ 1 là
2
15
C
. Số
đo n th ng t o nên t 18 đi m phân bi t trên dạ ẳ ạ ừ ể ệ 2 là
2
18
C
.
+ S tam giác có 2 đnh trên dố ỉ 1 và 1 đnh trên dỉ2 là:
2
15
C
.18 = 105.18 = 1890
+ S tam giác có 2 đnh trên dố ỉ 2 và 1 đnh trên dỉ1 là:
2
18
C
.15 = 153.15 = 2295
+ S tam giác c n tìm: 1890 + 2295 = 4185.ố ầ
0,25
0,25
0,25
0,25
4
1) + Tính đc t a đ đnh B(-5;-2)ượ ọ ộ ỉ
+ Tính đc t a đ đnh C(-1;4)ượ ọ ộ ỉ
+ V đng cao CH (Hẽ ườ
AB
). Tính đc t a đ đnh H ượ ọ ộ ỉ
2 1
;
5 5
� �
−
� �
� �
.
+ Tính đc di n tích tam giác ABC làượ ệ
1 1 7
S AB.CH .2 10. 10 14
2 2 5
= = =
.
0,25
0,25
0,25
0,25
2) + V hình đúng, tính đc di n tíchẽ ượ ệ
∆ABC là
2
ABC
1
S a
2
∆
=
.
+ Tính đc th tích kh i chópượ ể ố
S.ABC là
3
2
S.ABC
1 1 a
V . a .a
3 2 6
= =
.
+ G i h là kho ng cách t A đn m t ph ng (SBC) tính đc di nọ ả ừ ế ặ ẳ ượ ệ
0,25
0,25
3
S
AB
CD
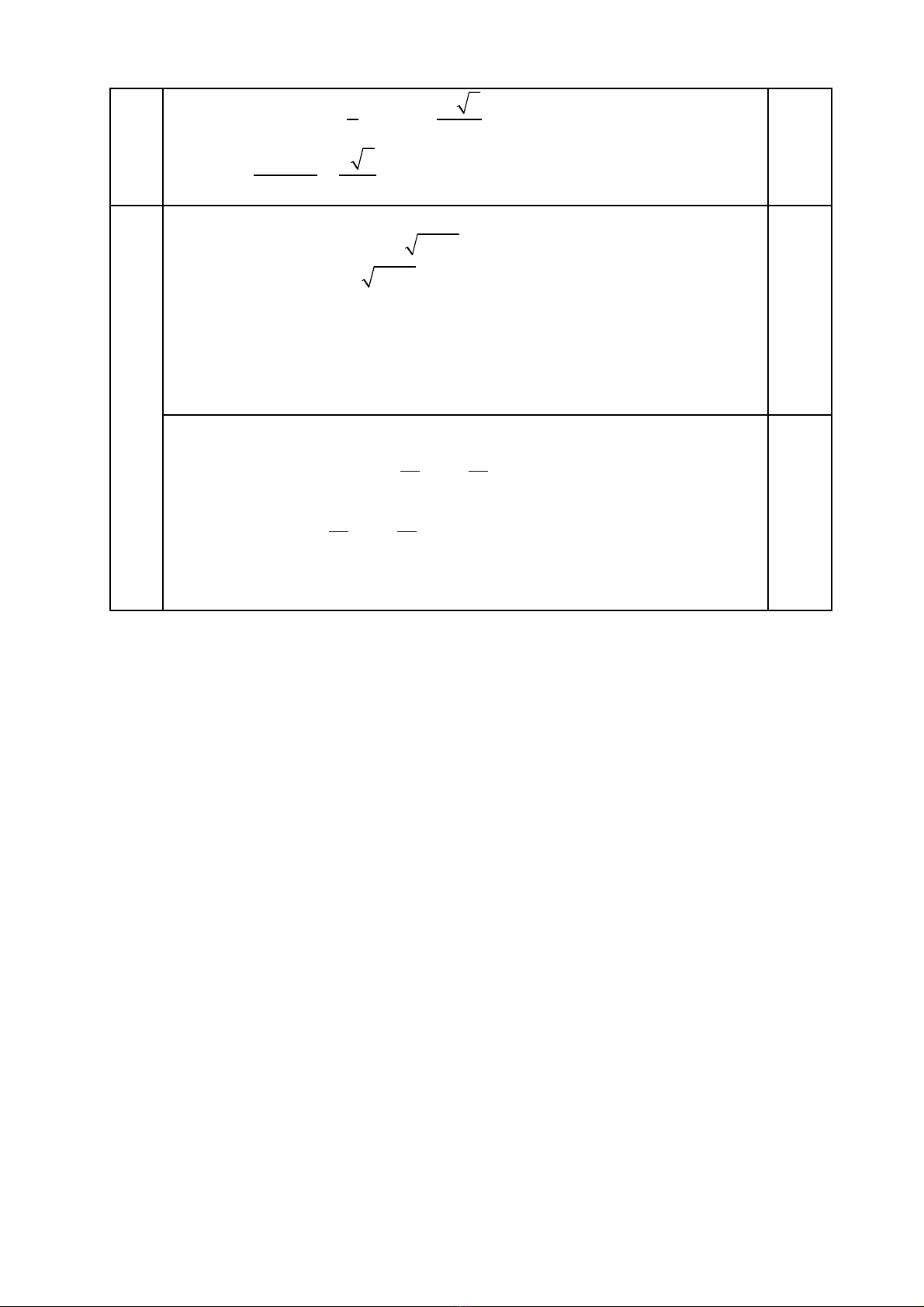
tích ∆SBC là
2
SBC
1 a 6
S SB.BC
2 2
∆
= =
.
+
S.ABC
SBC
3.V a 6
hS 6
∆
= =
0,25
0,25
5
1) + Đi u ki n: x > 0ề ệ
+ Ph ng trình: ươ
2 2
log x 2 log x+ =�
2
x 2 x
x 2 x
x 1
x 2
+ =�
+ =�
= −
=
0,25
0,25
0,25
0,25
2) + Chia 2 v cho 13ếx > 0,
x∀
đc b t ph ng trình t ng đng ượ ấ ươ ươ ươ
x x
5 12 1
13 13
� � � �
+ >
� � � �
� � � �
.
+ Đt f(x) = ặ
x x
5 12 f (x)
13 13
� � � �
+
� � � �
� � � �
là hàm ngh ch bi n trên ị ế
ﾡ
và
f(2) = 1 nên f(x) > f(2)
x < 2.
+ K t lu n: T p nghi m c a b t ph ng trình là (-ế ậ ậ ệ ủ ấ ươ
;2)
0,25
0,50
0,25
Chú ý: H c sinh gi i cách khác đúng v n cho đi m t i đa.ọ ả ẫ ể ố
4
(lo i)ạ
(nh n)ậ