
Nguyễn Đăng Quý
BỘ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH ĐẠI HỌC, CAO ĐẲNG
NĂM 2010
Môn: Toán. Khối A, B.
Thời gian làm bài: 180 phút (Không kể thời gian giao đề)
Câu I. (2 điểm). Cho hàm số 4 2 2
2 1
y x m x
(1).
1) Với m = 1, khảo sát và vẽ đồ thị của hàm số (1).
2) Tìm tất cả các giá trị m để đồ thị hàm số (1) có ba điểm cực trị A, B, C và diện
tích tam giác ABC bằng 32 (đơn vị diện tích).
Câu II. (2 điểm)
1) Giải phương trình: 2
3 2 1 2 4 3
x x x x x x
.
2) Giải phương trình lượng giác: 2
1 sin 2
1 tan2x
os 2
x
c x
.
Câu III. (1 điểm) Tính diện tích hình phẳng giới hạn bởi các đường sau:
cos
y x
và
2
2
3
4
y x x
Câu IV. (1 điểm)
Cho lăng trụ tam giác ABC.A1B1C1có tất cả các cạnh bằng a, góc tạo bởi cạnh bên
và mặt phẳng đáy bằng 300. Hình chiếu H của điểm A trên mặt phẳng (A1B1C1) thuộc
đường thẳng B1C1. Tính khoảng cách giữa hai đường thẳng AA1và B1C1theo a.
Câu V (1 điểm) Cho a, b, c là các số thực dương. Chứng minh rằng:
4 4
3
2 2
c a b
a b b c c a
Câu VI. (2 điểm)
1) Trong mặt phẳng tọa độ Oxy cho điểm M(3; 0), đường thẳng d1: 2x – y – 2 = 0,
đường thẳng d2: x + y + 3 = 0. Viết phương trình đường thẳng d đi qua M và cắt d1, d2 lần
lượt tại A và B sao cho MA = 2MB.
2) Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng (P): 5x – 4y + z – 6 = 0,
(Q): 2x – y + z + 7 = 0, đường thẳng d:
1 7
3
1 2
x t
y t
z t
. Viết phương trình mặt cầu (S) cắt (Q)
theo thiết diện là hình tròn có diện tích bằng
20
và có tâm là giao của d với (P) .
Câu VII. (1 điểm) Giải hệ phương trình :
23
2
2 16
log log ( )
y x
x y
y xy
--------------- HẾT ---------------
Đề thi thử lần 2
(Tháng 03 năm 2010)
Nguyễn Đăng Quý
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………….……. Số báo danh: ……………...
ĐÁP ÁN - THANG ĐIỂM
ĐỀ THI THỬ ĐẠI HỌC LẦN 2 TRƯỜNG THPT THANH OAI B
THÁNG 03 NĂM 2010
CÂU NỘI DUNG ĐIỂM
I.1
Với m = 1 hàm số là: 4 2
2 1
y x x
+) TXĐ: R
+) Giới hạn, đạo hàm:
lim lim
x x
y y
3
0
' 4 4 ; ' 0
1
x
y x x y x
+) BBT: x -
- 1 0 1
+
y' - 0 + 0 - 0 +
y +
1
+
0 0
+) Hàm số đồng biến trên các khoảng (- 1; 0), (1; +
); nghiechj biến trên
các khoảng
(-
; - 1), (0; 1)
Hàm đạt cực đại tại x = 0, yCĐ = 1, cực tiểu tại x =
1, yCT = 0
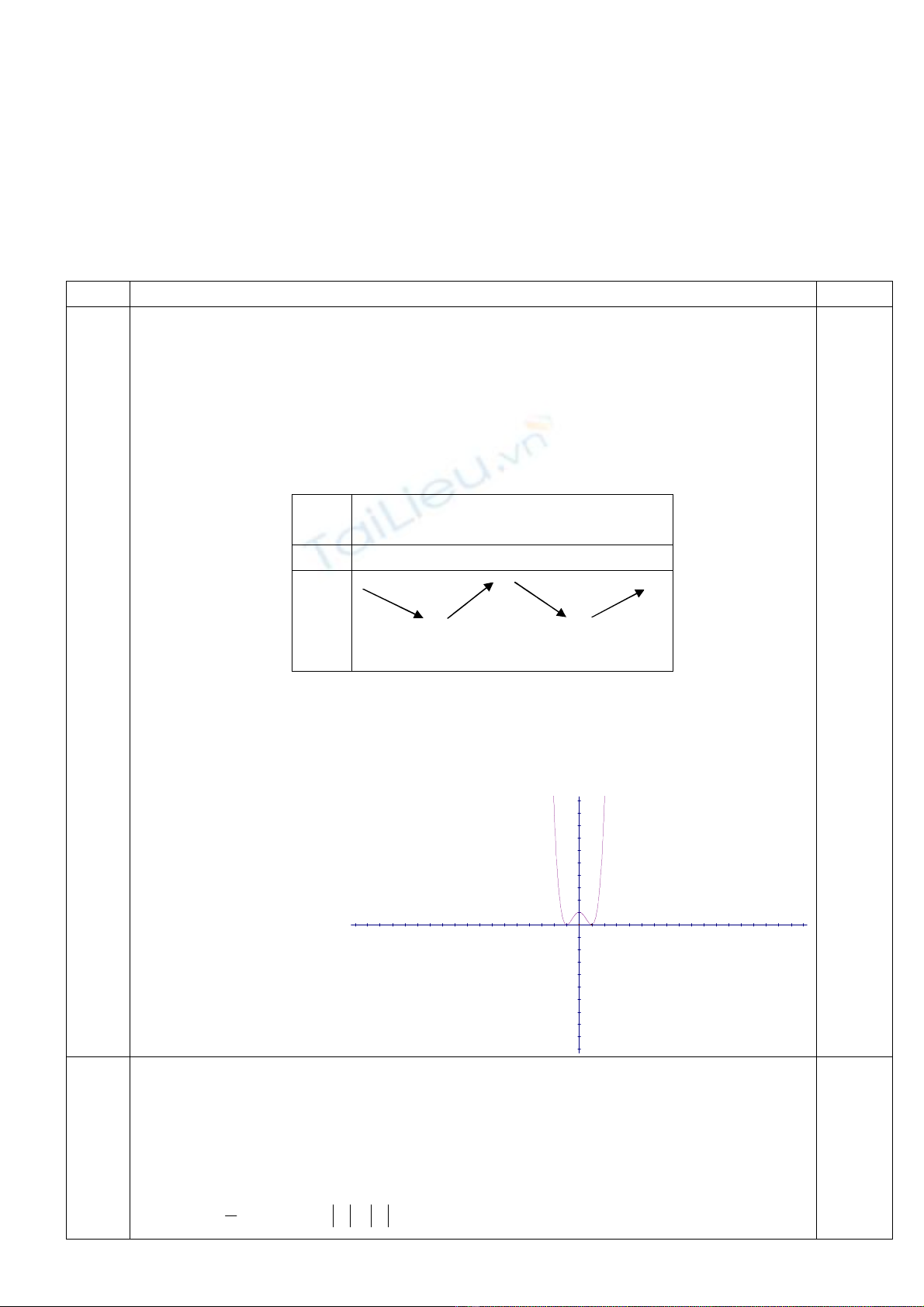
+) ĐT: Dạng đồ thị
10
8
6
4
2
-2
-4
-6
-8
-10
-15
-10 -5 5 10
15
0,25
0,25
0,25
0,25
I.2
+) Ta có y’ = 4x3– 4m2x ; y’ = 0
2 2
0
x
x m
; ĐK có 3 điểm cực trị : m
0
+) Tọa độ ba điểm cực trị : A(0 ; 1), B(- m ; 1 – m4), C(m ; 1 – m4) ;
+) CM tam giác ABC cân đỉnh A. Tọa độ trung điểm I của BC là I(0 ; 1 –
m4).
+) 5
4
1
. 32 2
2
ABC
S AI BC m m m m
(tm)
0,25
0,25
2,25
0,25
Nguyễn Đăng Quý
II.1
+) ĐK:
1
x
2
3 2 1 2 4 3 2 1 1 3 1 1 0
1 1 2 3 0
x x x x x x x x x x
x x x
0
0
1 1 0
( )
1 1
3 2 3/ 4
x
x
x x
tm
x x
x x
x
0,25
0,25
0,5
II.2
+) ĐK: ,
4 2
x k k Z
2
2
1 sin 2
1 t an2x os 2 sin 2 os2 1 sin 2
os 2
x
c x xc x x
c x
2
sin 2 sin 2 sin 2 . os2 0
x x x c x
sin 2 (sin 2 os2 1) 0
x x c x
sin 2 0 2
( , )
sin 2 os2 1 ;
2 4
x k
x
k l Z
x c x x l x l
+) Kết hợp ĐK ta được nghiệm của phương trình là
, ;( , )
2
x k x l k l Z
0,5
0,25
0,25
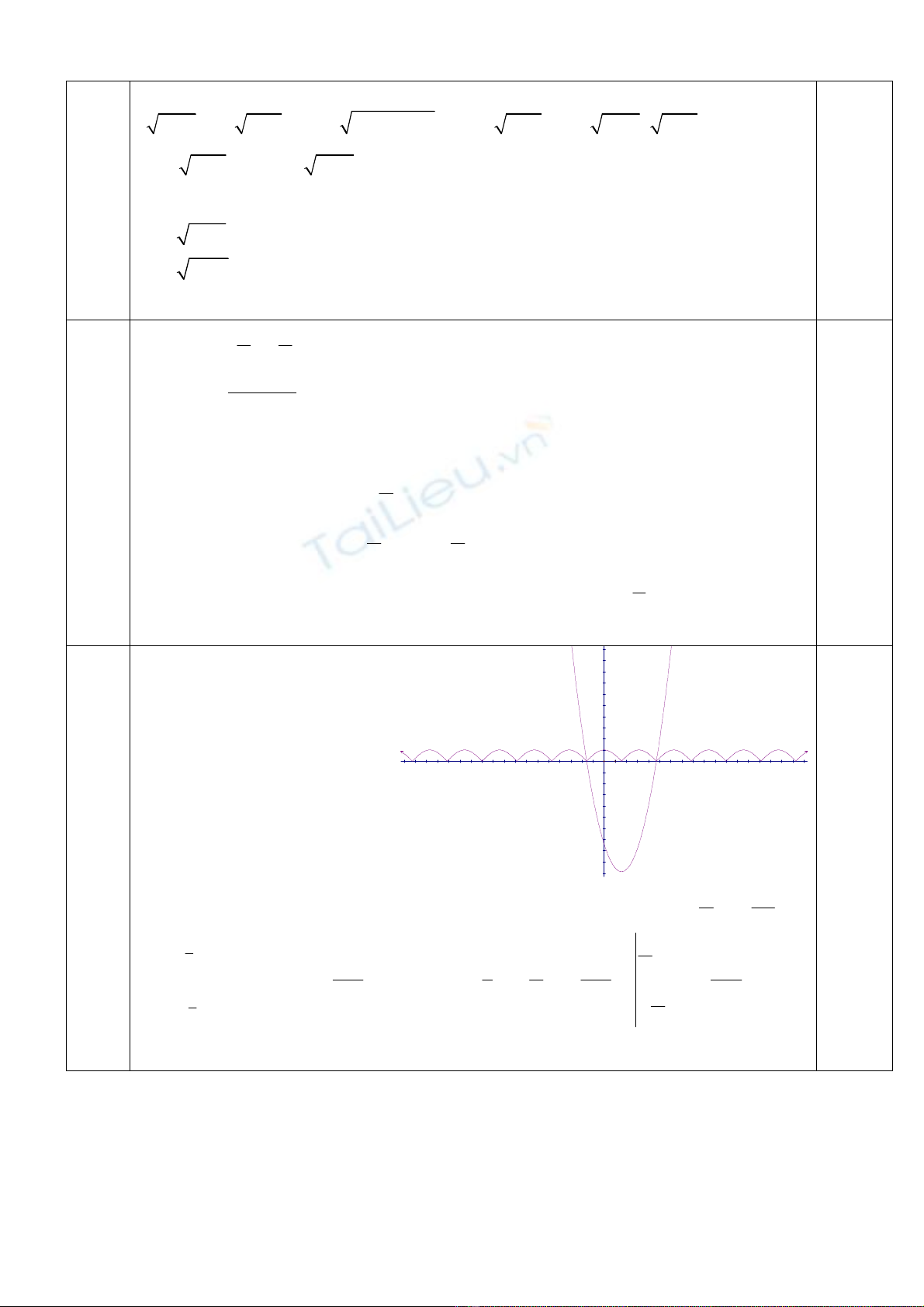
III
10
8
6
4
2
-2
-4
-6
-8
-10
-15
-10
-5
5
10
15
Chứng minh được hai đường có đúng hai giao điểm hoành độ
2
và
3
2
2 2 3
22 3 2
2
3 1 3 4
2
2 cos 2. sinx 4
4 3 2 4 3
2
S x x x dx x x x
0,25
0,25
0,5
Nguyễn Đăng Quý
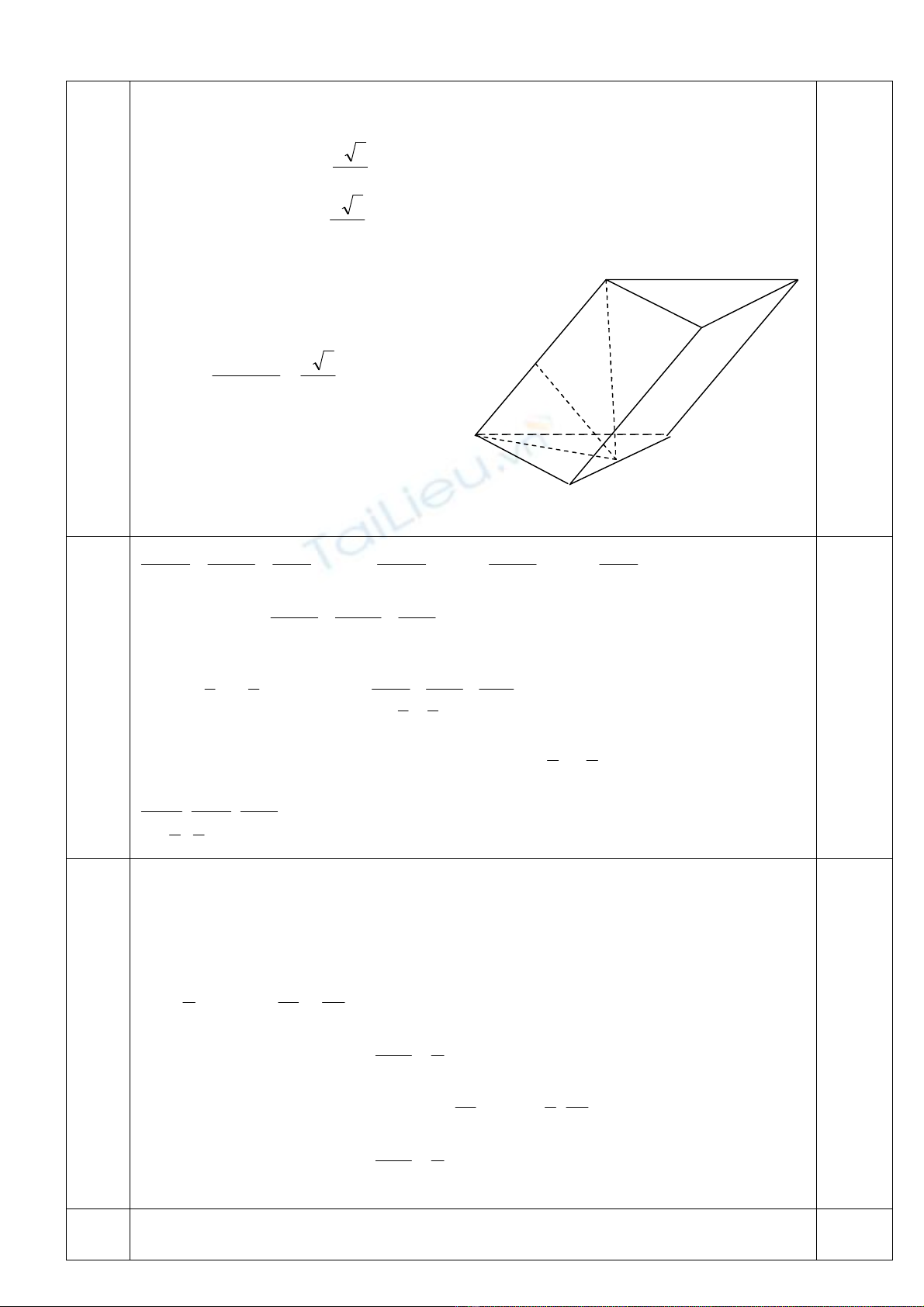
IV
Do )( 111 CBAAH nªn gãc HAA1
lµ gãc gi÷a AA1vµ (A1B1C1), theo gi¶
thiÕt th× gãc HAA1
b»ng 300. XÐt tam gi¸c vu«ng AHA1cã AA1= a, gãc
HAA1
=300
2
3
1a
HA . Do tam gi¸c A1B1C1lµ tam gi¸c ®Òu c¹nh a, H
thuéc B1C1vµ
2
3
1a
HA nªn A1H vu«ng gãc víi B1C1. MÆt kh¸c
11CBAH nªn )( 111 HAACB
KÎ ®-êng cao HK cña tam gi¸c AA1H
th× HK chÝnh lµ kho¶ng c¸ch gi÷a AA1vµ B1C1
Ta cã AA1.HK = A1H.AH
4
3
.
1
1a
AA
AHHA
HK
1
điểm
V
4 4 4 4
3 2 2 2 9
2 2 2 2
c a b c a b
a b b c c a a b b c c a
2 2 1
2 2 9
2 2
a b c a b b c c a
1 1 1
9
2 2 2 2
b b
a c c a b b c a
a c
+) Áp dụng BĐT Cô – si cho ba số dương
, ,
2 2
b b
a c c a
và
1 1 1
, ,
2 2
b b
c a
a c
rồi nhân hai BĐT cùng chiều ta có đpcm.
1
điểm
VI.1
+) Dạng tham số của d1và d2:1 2
: , :
2 2 3
x t x u
d d
y t y u
+) Tọa độ A(t; - 2 + 2t), B(u; - 3 – u).
3; 2 2 ; 3; 3
MA t t MB u u
+) TH1:
2.
MA MB
: Tìm được
7 16 20
, ; : 4;5
3 3 3 d
t MA VTCPd u
3
: 5 4 15 0
4 5
x y
d x y
+) TH2:
2.
MA MB
: Tìm được
17 8 28
, ; : 2;7
3 3 3 d
t MA VTCPd u
3
: 7 2 21 0
2 7
x y
d x y
0,25
0,25
0,25
0,25
VI.2 +) Tâm I của mặt cầu là giao của d và (P) nên tọa độ I là nghiệm của hệ
phương trình:
A
A
B
C
C
B
1
K
H

Nguyễn Đăng Quý
1 7 0
3 1
(1;0;1)
1 2 0
5 4 6 0 1
x t t
y t x I
z t y
x y z z
+) Gọi h là khoảng cách từ I đến mp(Q), ta có:
2
222
2.1 0 1 7
10 50
3
6
2 ( 1) ( 1)
h h
+) Thiết diện của (Q) với mặt cầu (S) là hình tròn có diện tích bằng
2 2
20 20 . 20
r r
(r là bán kính hình tròn)
+) Gọi R là bán kính mặt cầu (S), ta có 2 2 2
50 110
20
3 3
R h r
Suy ra phương trình mặt cầu (S):
2 2
2
110
1 1
3
x y z
0,25
0,25
0,25
0,25
VII
+) ĐK:
0 1,0 1
x y
+)
22
3
2
3 4 (1)
2 16
2log 1 log (2)
log log ( )
y x
x y
x y
y x
y x
y xy
+) Đặt 2
2
1
1
log (2):2 1 2 1 0 1
2
x
t
x y
y t t t t
tt
x y
+) Với x = y, kết hợp (1) ta được x = y = 1 (loại) và x = y = 3 (nhận).
+) Với x = y-2, kết hợp với (1) ta được y2 = 1 (loại), y = - 4 (loại)
Vậy hệ đã cho có nghiệm duy nhất x = y =3.
0,25
0,25
0,25
0,25
Ghi chú: - Các cách giải khác với cách giải trong đáp án mà vẫn đúng, đủ thì cũng cho
điểm tối đa.






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



