Sở giáo dục & đào tạo Nghệ An
Trường THPT Anh Sơn I
************
Kì thi thử Đại học & cao đẳng lần thứ 1
Năm học 2010-1011
Môn Toán – Thời gian 180’
************
Họ và tên : ……………………………….Số báo danh : …………………………
Câu I : Cho hàm số
( )
2
2
1
2
y x m
= − +
a) Kh
ả
o sát và v
ẽ
đồ
th
ị
hàm s
ố
đ
ã cho v
ớ
i
1
m
= −
b) Tìm m
để
đồ
th
ị
hàm s
ố
có 3
đ
i
ể
m c
ự
c tr
ị
và 3
đ
i
ể
m c
ự
c tr
ị
đ
ó cùng n
ằ
m trên m
ộ
t
đườ
ng tròn có bán kính
5
4
R
=
.
Câu II:
1) Gi
ả
i b
ấ
t ph
ươ
ng trình :
)
)
( )
3 1 2 2 3 2 5 2
x x x x x
+ + − + + − > +
2) Gi
ả
i h
ệ
ph
ươ
ng trình :
)
2
2 2
2 1
2
y xy x y x y
x y
− + − = − +
+ =
Câu III:
1) Gi
ả
i ph
ươ
ng trình :
3 2cos
tan 3
1 2sin
x
x
x
−
=+
2) Khai tri
ể
n
20
1 2
2 3
x
+
thành
đ
a th
ứ
c
2 20
0 1 2 20
...
a a x a x a x
+ + + + . Trong các c
ặ
p s
ố
(
)
1
;
i i
a a
+
v
ớ
i
0;1;2;...;19
i
=
, c
ặ
p s
ố
nào có t
ổ
ng l
ớ
n nh
ấ
t ?
Câu IV:
1) Trong m
ặ
t ph
ẳ
ng t
ọ
a
độ
Oxy
, cho tam giác
ABC
v
ớ
i
đỉ
nh
(
)
2;2
A
, m
ộ
t
đườ
ng cao có
ph
ươ
ng trình
6 29 0
x y
+ − =
. Tìm t
ọ
a
độ
đỉ
nh B và
đỉ
nh C bi
ế
t t
ọ
a
độ
tr
ọ
ng tâm tam giác ABC
là
14 10
;
3 3
G
và
AB AC
<
.
2) Cho hình chóp t
ứ
giác S.ABCD có
đ
áy ABCD là hình vuông c
ạ
nh a và hình chi
ế
u vuông
góc c
ủ
a S trên mp(ABCD) trùng v
ớ
i tr
ọ
ng tâm G tam giác ABC. Kho
ả
ng cách t
ừ
trung
đ
i
ể
m I
c
ủ
a
đ
o
ạ
n AB
đế
n m
ặ
t ph
ẳ
ng (SCD) b
ằ
ng
2
a
. Tính th
ể
tích hình chóp S.ABCD theo a.
Câu V:
1) Tìm nguyên hàm :
( )
3ln 2
ln 3ln 2
x
dx
x x x
−
− −
∫
2) Cho
1 0
x
≠ >
, chứng minh rằng :
3
3
ln 1
1
x x
x
x x
+
≤
−+
----------------HẾT-----------------
Đáp án và hướng dẫn chấm thi thử lần 1 – năm học 2010-2011
Môn Toán (gồm 6 trang )
(Lưu ý : các cách khác đáp án , nhưng đúng thì vẫn cho điểm tối đa )
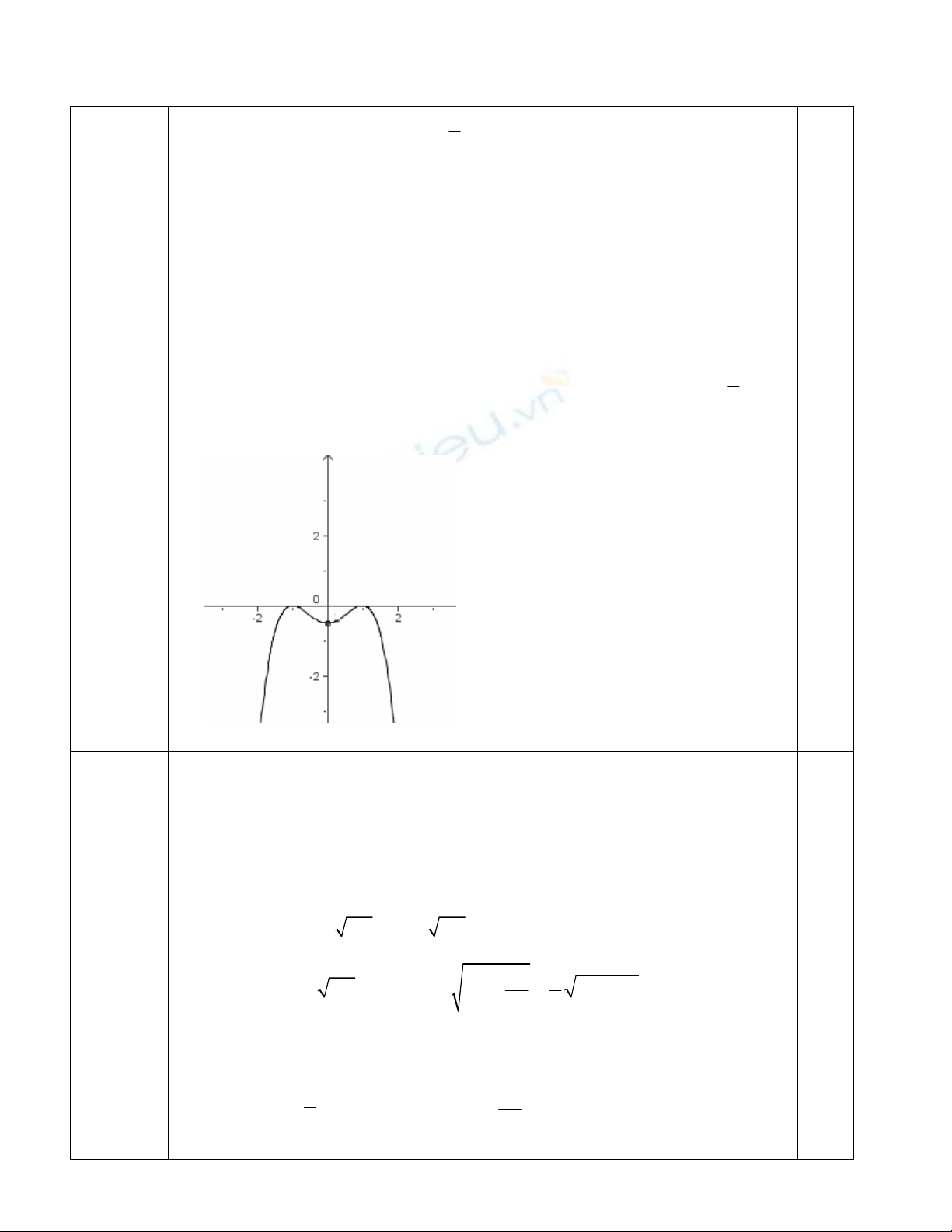
Câu I.1
( 1 điểm ) Với m = -1 hàm số trở thành :
( )
2
2
1
1
2
y x
= − −
• TXĐ:
D R
=
•
Giới hạn :
lim ; lim
x x
y y
→+∞ →−∞
= −∞ = −∞
•
S
ự
bi
ế
n thiên :
( )
2
0
' 2 1 ; ' 0 1
1
x
y x x y x
x
=
= − − = ⇔ = −
=
Hàm s
ố
đồ
ng bi
ế
n trên các kho
ả
ng
(
)
(
)
; 1 , 0;1
−∞ −
, ngh
ị
ch bi
ế
n trên các
kho
ả
ng
(
)
(
)
1;0 ; 1;
− +∞
.
Hàm s
ố
đạ
t c
ự
c
đạ
i t
ạ
i
1
x
= ±
,
0
CD
y
=
,
đạ
t c
ự
c ti
ể
u t
ạ
i
1
0;
2
CT
x y
= = −
•
B
ả
ng bi
ế
n thiên :
•
Đồ
th
ị
:
Nh
ậ
n xét :
đồ
th
ị
có tr
ụ
c
đố
i x
ứ
ng là Oy
0,25
0,25
0,25
0,25
Câu I.2
( 1 điểm )
•
TX
Đ
: D = R
•
Đạ
o hàm :
( )
2
2
0
' 2 , ' 0 x
y x x m y
x m
=
= − + = ⇔
= −
•
Đồ
th
ị
hàm s
ố
b
ậ
c 4 trùng ph
ươ
ng có 3
đ
i
ể
m c
ự
c tr
ị
khi và ch
ỉ
khi y’ = 0
có 3 nghi
ệ
m phân bi
ệ
t . V
ậ
y
đ
i
ề
u ki
ệ
n
0
m
<
•
T
ọ
a
độ
các
đ
i
ể
m c
ự
c tr
ị
đ
ó là :
( ) ( )
2
0; , ;0 , ;0
2
m
A B m C m
− − − −
Ta có :
44
1
2 , 4
4 2
m
BC m AB AC m m m
= − = = − + = −
Bán kính
đườ
ng tròn ngo
ạ
i ti
ế
p tam giác ABC là :
( )
4
2 2 3
2
14
. 4
4
1
4 2 4
4. . 2.
2
2
m m
abc AB BC AB m
Rm
S AH m
BC AH
−
−
= = = = =
0,25
0,25
0,25
Theo yêu c
ầ
u bài ra :
( )
( )
33
2
5 4 5 5 4 0
4
1
1 4 0
1 17
2
m
R m m
m
m
m m m
m
−
= ⇔ = ⇔ − − =
= −
⇔ + − − = ⇔ ±
=
Do m < 0 nên đáp số là :
1 17
1,
2
m m −
= − =
0,25
Câu II.1
( 1 điểm ) • ĐK : 1
2
3
x
− ≤ ≤
• Với đk trên ta có :
1 1
2 3 2 2 3 2 0
3 3
x x
+ − − ≥ − + − + >
, nên nhân
hai vế bất pt với
)
2 3 2
x x
+ − −
ta được bpt tương đương :
)
( ) ( )
)
3 1 2 5 10 5 2 2 3 2
x x x x x x
+ + − + > + + − −
3 1 2 2 3 2
x x x x
⇔ + + − > + − −
( do
5 10 0
x
+ >
)
( )( ) ( ) ( )
( )( )
3 1 2 2 2 3
3 1 4 3 1 2 4 2 4 3
4 3 1 2 5 3
x x x
x x x x x
x x x
⇔ + + − > +
⇔ + + + − + − > +
⇔ + − > +
( do 5x + 3 > 0 )
(
)
(
)
2
2
16 3 1 2 25 30 9
73 50 23 0
23 1
73
x x x x
x x
x
⇔ + − > + +
⇔ − − <
⇔ − < <
•
K
ế
t h
ợ
p v
ớ
i
đ
k ban
đầ
u , b
ấ
t pt có nghi
ệ
m : 23
1
73
x
− < <
0,25
0,25
0,25
0,25
Câu II.2
( 1 điểm )
T
ừ
pt th
ứ
2 c
ủ
a h
ệ
ta có :
2 2
2
x y
= −
Thay vào pt th
ứ
nh
ấ
t :
)
(
)
2
1 1 1
1
1 0
y x xy x x y xy x y x y
xy
x y
− + − = − + ⇔ − + = − +
=
⇔
− + =
•
Xét TH :
1
1xy y
x
= ⇔ =
Thay vào pt th
ứ
2 ta có :
2
2
1
2 1
x x
x
+ = ⇔ = ±
.
V
ậ
y TH này h
ệ
có hai nghi
ệ
m
(
)
(
)
1; 1 , 1; 1
x y x y
= − = − = =
•
Xét TH :
1 0 1
x y y x
− + = ⇔ = +
. Thay vào pt th
ứ
2 c
ủ
a h
ệ
ta có :
( )
2
2 2
1 3
1 2 2 2 1 0
2
x x x x x − ±
+ + = ⇔ + − = ⇔ = . V
ậ
y TH này h
ệ
có 2
nghi
ệ
m :
1 3 1 3 1 3 1 3
; , ;
2 2 2 2
x y x y
− − − − + +
= = = =
• Tóm lại hệ có các nghiệm :
(
)
(
)
1; 1 , 1; 1
x y x y
= − = − = =
,
0,5
0,25
1 3 1 3 1 3 1 3
; , ;
2 2 2 2
x y x y
− − − − + +
= = = =
0,25
Câu III.1
( 1 điểm )
• ĐK :
( )
6 3
cos3 0 2 , , ,
1 2sin 0 6 6 3
72
6
x k
x
x m k m n Z x k k Z
x
x n
π π
π π π
π
ππ
≠ +
≠
⇔ ≠ − + ∈ ⇔ ≠ + ∈
+ ≠
≠ +
• Với đk trên , pt đã cho tương đương với pt :
( )
)
( )
sin 3 1 2sin cos3 3 2 cos
3 cos 3 sin 3 2sin 3 sin 2cos3 cos
3 cos 3 sin 3 2 cos 2
cos 3 cos 2
6
3 2 2
6
x x x x
x x x x x x
x x x
x x
x x l l Z
π
ππ
+ = −
⇔ − = +
⇔ − =
⇔ + =
⇔ + = ± + ∈
( )
2
6
2
30 5
x l
l Z
x l
ππ
π π
= − +
⇔ ∈
= − +
Đối chiếu đk ban đầu, ta thấy pt có nghiệm :
( )
2,
30 5
x l l Z
π π
= − + ∈
0,25
0,25
0,25
0,25
Câu III.2
( 1 điểm )
Áp dụng công thức khai triển nhị thức Newton ta có :
20 20 20
20 20
20 20
0 0
1 2 1 2 1 2
2 3 2 3 2 3
k k k k
k k k
k k
x C x C x
− −
= =
+ = =
∑ ∑
Vậy
( )
20
20
1 2
, 0,1,...,20
2 3
k k
k
k
a C k
−
= =
Với k = 0;1;2;…;19 ta có :
( )
( )
( )
( )
19 1
1
20
1
20
20
1 2 2
20 . 4 20
2 3 3
1
3 1
1 2 1 . 2
2 3
k k
k
k
k k
kk
Ck
k
a
a k
k
C
− +
+
+
−
−
−
= = = +
+
( ) ( )
1
1
1 4 20 3 1 11
k
k k
k
a
a a k k k
a
+
+
< ⇔ > ⇔ − > + ⇔ <
1
11
k k
a a k
+
> ⇔ >
Từ đó suy ra :
0 1 2 11 12 13 20
... ...
a a a a a a a
< < < < = > > >
Vậy cặp số lớn nhất là
(
)
11 12
;
a a
0,25
0,25
0,25
0,25
Câu IV.1
( 1 điểm )
Đường cao
6 29 0
x y
+ − =
không đi qua A, nên nó đi qua B hoặc C.
Ta xét TH nó đi qua B.
Đường thẳng AC đi qua A(2;2) và vuông góc với đường cao
6 29 0
x y
+ − =
nên
0,25
có phương trình :
(
)
(
)
1 2 6 2 0 6 10 0
x y x y
− − − = ⇔ − + =
(AC)
Gọi tọa độ
(
)
(
)
;29 6 , 6 10;
B b b C c c
− −
Tọa độ trọng tâm là :
6 10 2 14
6 22 4
3 3
29 6 2 10 6 21 3
3 3
b c
b c b
b c b c c
+ − +
=
+ = =
⇔ ⇔
− + + − + = − =
=
Suy ra
(
)
(
)
4;5 , 8;3
B C
, kiểm tra thấy
13 37
AB AC= < =
Xét TH đường cao
6 29 0
x y
+ − =
đi qua C, khi đó
(
)
(
)
4;5 , 8;3
C B
không thỏa
mãn đk
AB AC
<
Vậy đáp số bài toán là :
(
)
(
)
4;5 , 8;3
B C
0,25
0,25
0,25
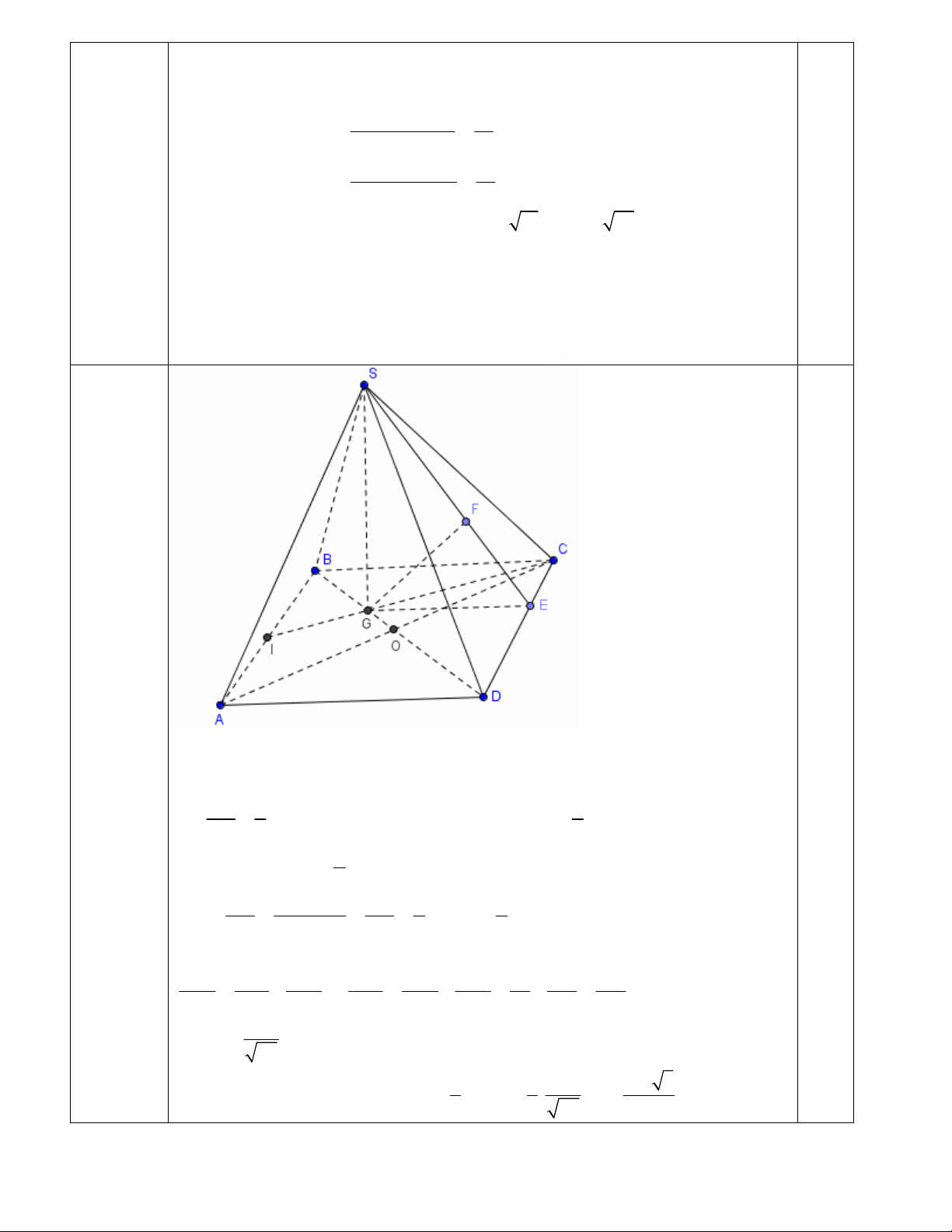
Câu IV.2:
( 1 điểm )
Trong mp(ABCD) kẻ GE vuông góc với CD. Trong mp(SGE) kẻ GF vuông góc
với SE ( hình vẽ )
Khi đó khoảng cách từ G đên mp(SCD) bằng đoạn GF
Do
2
3
GC
IC
=
nên khoảng cách từ G đến (SCD) bằng
2
3
khoảng cách từ I đến
(SCD) , do đó
3
a
GF
=
.
Ta có
( )
2 2
, 3 3
GE GE GC
GE a
AD d I CD IC
= = =
⇒
=
Trong tam giác vuông SGE ta có :
2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 9 9 27
4 4
GF GS GE GS GF GE a a a
= +
⇒
= − = − =
2
27
a
GS
⇒
=
Vậy thể tích hình chóp là :
3
2 2
.
1 1 2 2 3
. . .
3 3 27
27
S ABCD
a a
V SG a a= = =
0,25
0,25
0,25
0,25