TRƯỜNG THCS TÂN HỘI ĐỀ THI THỬ VÀO LỚP 10
MÔN: TOÁN
Năm học: 2021-2022
Thời gian làm bài: 120 phút
Bài I : (2 điểm) Cho hai biểu thức A =
1
1
x
x
−
+
và B =
15 2 1
:
25 5 5
x x
xx x
− +
+
−+ −
(Với x 0 và x 25)
1. Tính giá trị của A tại x = 9;
2. Rút gọn B;
3. Tìm m để phương trình A – B = m có nghiệm.
Bài II :(2,5 điểm)
1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Hai tổ sản xuất cùng làm chung một công việc thì sau 12 ngày xong. Nếu tổ I làm
một mình trong 7 ngày, tổ II làm một mình trong 2 ngày thì cả hai tổ làm xong một
nửa công việc. Tính thời gian mỗi tổ làm một mình xong toàn bộ công việc.
2. Để cứu một người ở ban công tầng 3 của một ngôi nhà bị hỏa hoạn, người ta bắc
một chiếc thang AB. Biết độ cao ban công HB =12m và thang tạo với mặt đất góc
ﾶ
0
72BAH
=
Tính độ dài của thang (làm tròn đến cm).
Bài III: (2,0 điểm)
1. Cho hệ phương trình:
2.
2 1
x my
mx y
− =
+ =
a) Giải hệ phương trình với
3m
=
b) Tìm
m
để hệ phương trình đã cho có nghiệm duy nhất
( ; )x y
sao cho
0;x y
+ >
2. Cho 3 đường thẳng
,
2
( ) : 2 1d y x= +
,
2
3
( ) : (m 1)d y x m
= + +
Tìm m để 3 đường thẳng đồng quy.
Bài IV : (3, 0 điểm)
Cho đường tròn (O; R) có đường kính AB. Điểm H nằm giữa A và O. Dây CD
vuông góc với AB tại H. Lấy E nằm giữa H và C. Các tia AE, BE cắt đường tròn
(O) thứ tự tại M và N
( )
,N
Μ Α Β
. Đường thẳng AN cắt CD tại I.
1) Chứng minh bốn điểm A,H,E,N cùng thuộc một đường tròn và B, M, I thẳng
hàng ;
2) Chứng minh AN.AI = AH.AB và AN.AI + BM.BI = 4R2;
3) Chứng minh rằng khi H thay đổi trên đoạn thẳng OA (H vẫn nằm giữa O và A)
thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.
Bài V: (0,5 điểm) Giải phương trình
( )
( )
2 2
2 1 1 1x x x x
− − = + +
------------------------ HẾT -----------------------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh ......................................... Số báo danh .............................
HƯỚNG DẪN CHẤM ĐỀ THI THỬ VÀO LỚP 10 THPT LẦN 1
Năm học: 2020 - 2021
Bài Câu NỘI DUNG Biểu
điểm
Bài I
(2,0 đ)
1
(0,5đ)
Thay được x = 9 vào biểu thức A 0,25
Tính được A =
1
2
và kết luận 0,25
2
(1đ) Rút gọn được B =
1
1x+
1,0
3
(0,5đ) Với x 0 và x 25 thì A - B = m
(m+1)
x
= - m 0,25
Trường hợp 1: Với m = -1: Phương trình vô nghiệm
Trường hợp 2: Với m ≠-1: Phương trình có dạng
1
m
xm
−
=+
Phương trình này có nghiệm thỏa mãn x 0 và x 25
0
1
5
1
m
m
m
m
−
+
−
+
1 0
5
6
m
m
− <
−
0,25
Bài II
(2,5 đ)
1
(2,0đ)
Gọi thời gian tổ I làm một mình xong công việc là x (ngày), đk:
x > 12
Gọi thời gian tổ II làm một mình xong công việc là y (ngày),
đk: y > 12
0,25
Một ngày tổ I làm được
1
x
(công việc), tổ II làm được
1
y
(công
việc)
Vì cả hai tổ cùng làm trong 12 ngày thì xong công việc nên 1
ngày cả hai tổ làm được
1
12
(công việc), ta có pt:
1 1 1
12x y
+ =
(1)
0,5
Vì tổ I làm trong 7 ngày, tổ II làm tiếp trong 2 ngày thì cả hai tổ
làm được một nửa công việc nên ta có phương trình:
7 2 1
2x y
+ =
(2)
Từ (1) và (2) ta có hpt:
1 1 1
12
7 2 1
2
x y
x y
+ =
+ =
Giải hpt tìm ra được x = 15 (TMĐK) và y = 60 (TMĐK)
Vậy tổ I làm một mình trong 15 ngày thì xong công việc, tổ II
làm một mình trong 60 ngày thì xong công việc
0,5
0,5
0,25
Ta có : BH=ABsinA
12 .sin 72AB
=
0,25
2
(0,5 đ)
12 1262( )
sin 72
AB cm
=
0.25
Bài III
(2,0 đ)
1(1đ) a) Thay m=3 giải được nghiệm của hệ phương trình là
7 5
( ; )
11 11
−
0,5
b) * Hệ phương trình có nghiệm với mọi
.m
* Giải hệ:
2
2
4
2.
1 2
2
m
xm
m
ym
+
=
+
−
=
+
*
0x y
+ <
ta có:
2 2 2
4 1 2 5 0
2 2 2
5 0
5
m m m
m m m
m
m
+ − − +
+ = <
+ + +
− + <
>
0,25
0,25
2
(1đ) Tìm được tọa độ giao điểm của
1
( ) : 2d y x= +
,
2
( ) : 2 1d y x= +
là (1; 3) 0,5
Lập luận tìm được m=-2 0,5
Bài IV
(3,0 đ)
1
(1,25
đ)
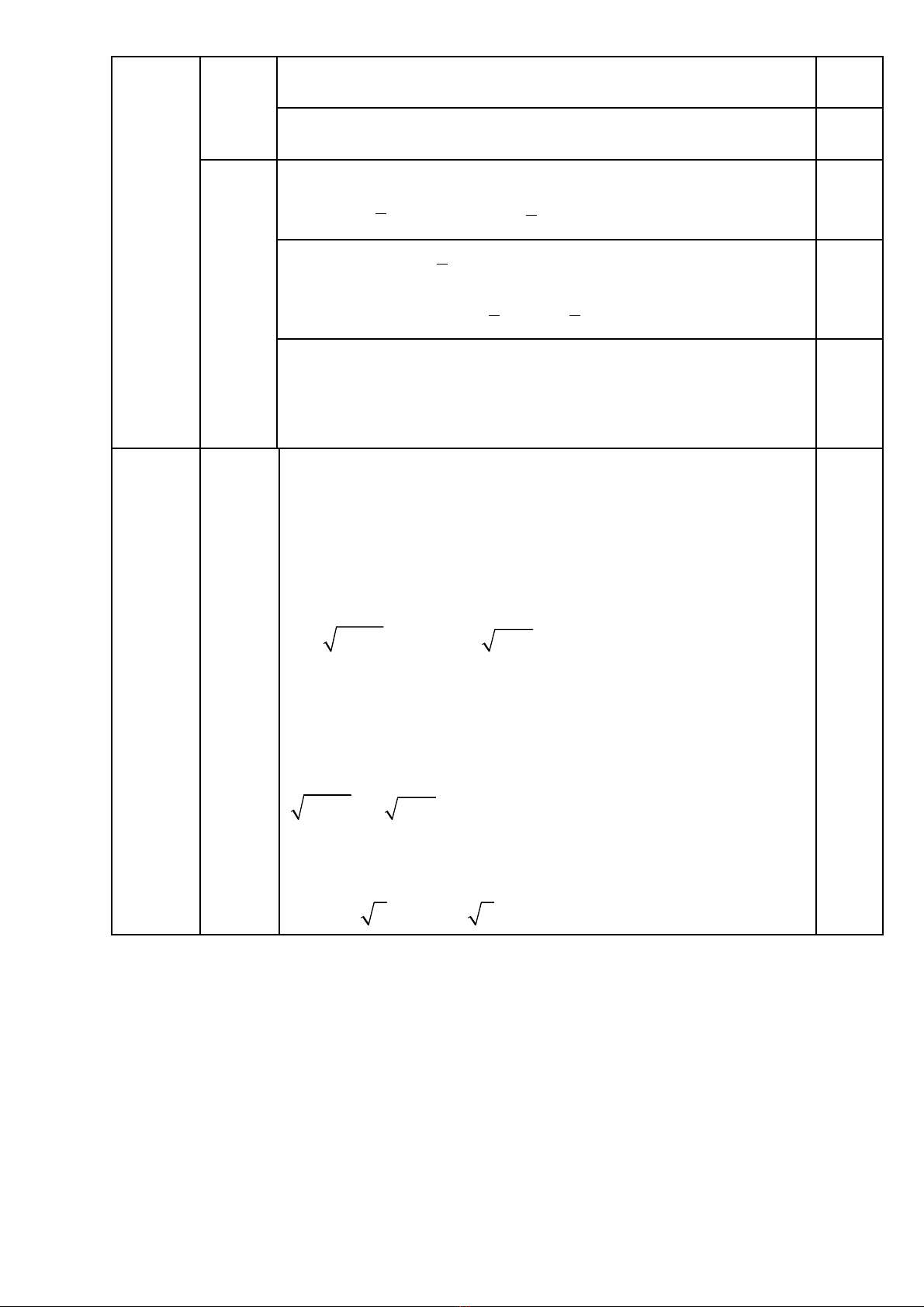
Vẽ hình đúng đến câu 1
C
I
N
M
D
O
A
B
H
E
0,25
ﾶ
0
90ANB
=
(góc nội tiếp chắn nửa đường tròn)
ﾶ
0
90ANE
=
ﾶ
0
90AHE =
(gt
CD AB
⊥
tại H) 0,25
Chứng minh bốn điểm A,H,E,N cùng thuộc một đường tròn 0,25
Có
ﾶ
0
90AMB =
( góc nội tiếp chắn nửa đường tròn)
BM AE
⊥
IAB
∆
có
( ), ( )BN AI cmt IH AB gt
⊥ ⊥
BN cắt IH tại E
E là trực tâm
AE BI
⊥
0,25
, , ,BM AE BI AE B M I
⊥ ⊥
thẳng hàng 0,25
2
(1,0
đ)
( . )AHI ANB g g
∆ ∆
:
0,25
. .
AH AI AN AI AH AB
AN AB
= =
0,25
Chứng minh tương tự
. .BM BI BH AB
=
0,25
( )
2
. . . . 2 .2 4AN AI BM BI AH BH AB AB AB R R R
+ = + = = =
0,25
3
(0,75
đ)
Vì AHEN là tứ giác nội tiếp
Mà
?
?
=1
2
NAE sñMN
ﾶ
ﾶ
1
2
NHE sñMN =
0,25
Tương tự:
ﾶ
ﾶ
1
2ñ=EHM s MN
ﾶ
ﾶ
ﾶ
ﾶ ﾶ ﾶ
1 1
2 2
NHM NHE EHM sñMN sñMN sñMN = + = + =
0,25
Có
?
?
=
NOM sñMN
(góc ở tâm)
ﾶ ﾶ
ﾶ
( )NOM NHM sñMN = =
N, H, O, M cùng thuộc một đường tròn
đường tròn ngoại tiếp tam giác HMN đi qua O cố định.
0,25
Bài V
(0,5 đ) ĐKXĐ :
1x
−
*Nhận xét :
2 2
2 1 ( 1) 2( 1)x x x x− − = + − +
Đặt
2
1( 0), 1( 0)a x a b x b= + > = +
Từ (1) ta có pt :
2 2 2 2
2 2 0
( )( 2 ) 0
2 0
a b ab a b ab
a b a b
a b
− = − − =
+ − =
− =
vì a + b > 0
2 2
2
1 2 1 1 4( 1)
4 3 0
x x x x
x x
+ = + + = +
− − =
Giải pt tìm và trả lời được pt có hai nghiệm là
1 2
2 7; 2 7x x
= + = −
0.25
0.25
- Học sinh vẽ sai hình không chấm
- Học sinh làm đúng theo cách khác cho điểm tương đương