PHÒNG GD&ĐT HOA LƯ
TRƯỜNG THCS ĐINH TIÊN HOÀNG
ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN
Năm 2024
MÔN: TOÁN
Thời gian làm bài: 150 phút
(Đề thi gồm 05 câu, 01 trang)
MA TRẬN ĐỀ THI
TT Nội dung kiến thức
Mức độ nhận thức Tổng Tỉ lệ
%
tổng
điểm
Thông hiểu Vận dụng Vận dụng cao
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
1Rút gọn, tính giá trị
biểu thức 1 1 10 1 1 10 10
2Hệ Phương trình 1 1 10 1 1 10 10
3Đa thức 1 1 10 1 1 10 10
4Bất đẳng thức 1 1 25 1 1 25 10
5Số học 1 0,75 10 1 0,75 15 2 1,5 25 15
6Hình học phẳng 1 1 10 1 1 10 1 1 15 3 3 35 30
7Tổ hợp 2 1,5 10 2 1,5 25 15
BẢN ĐẶC TẢ ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN
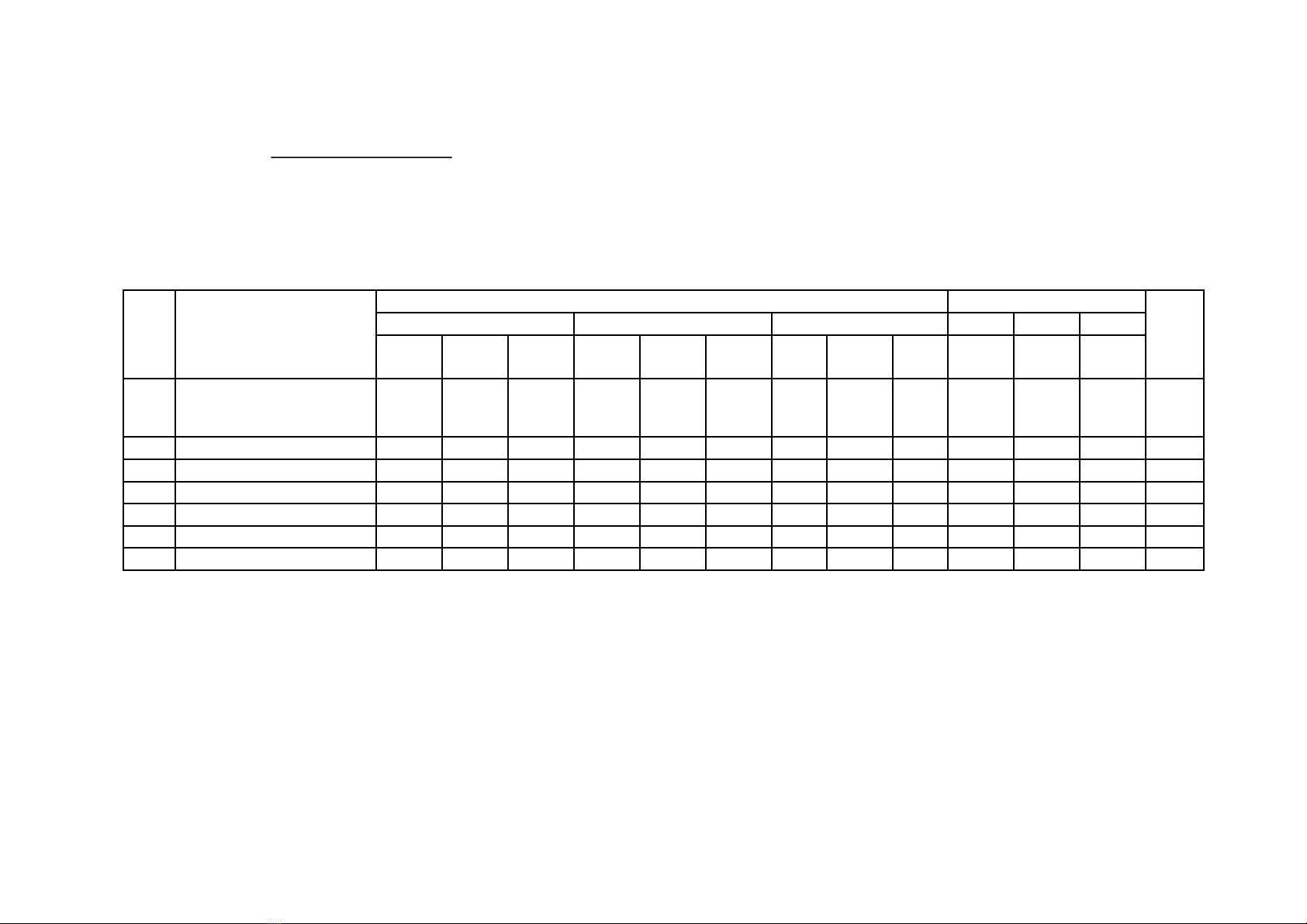
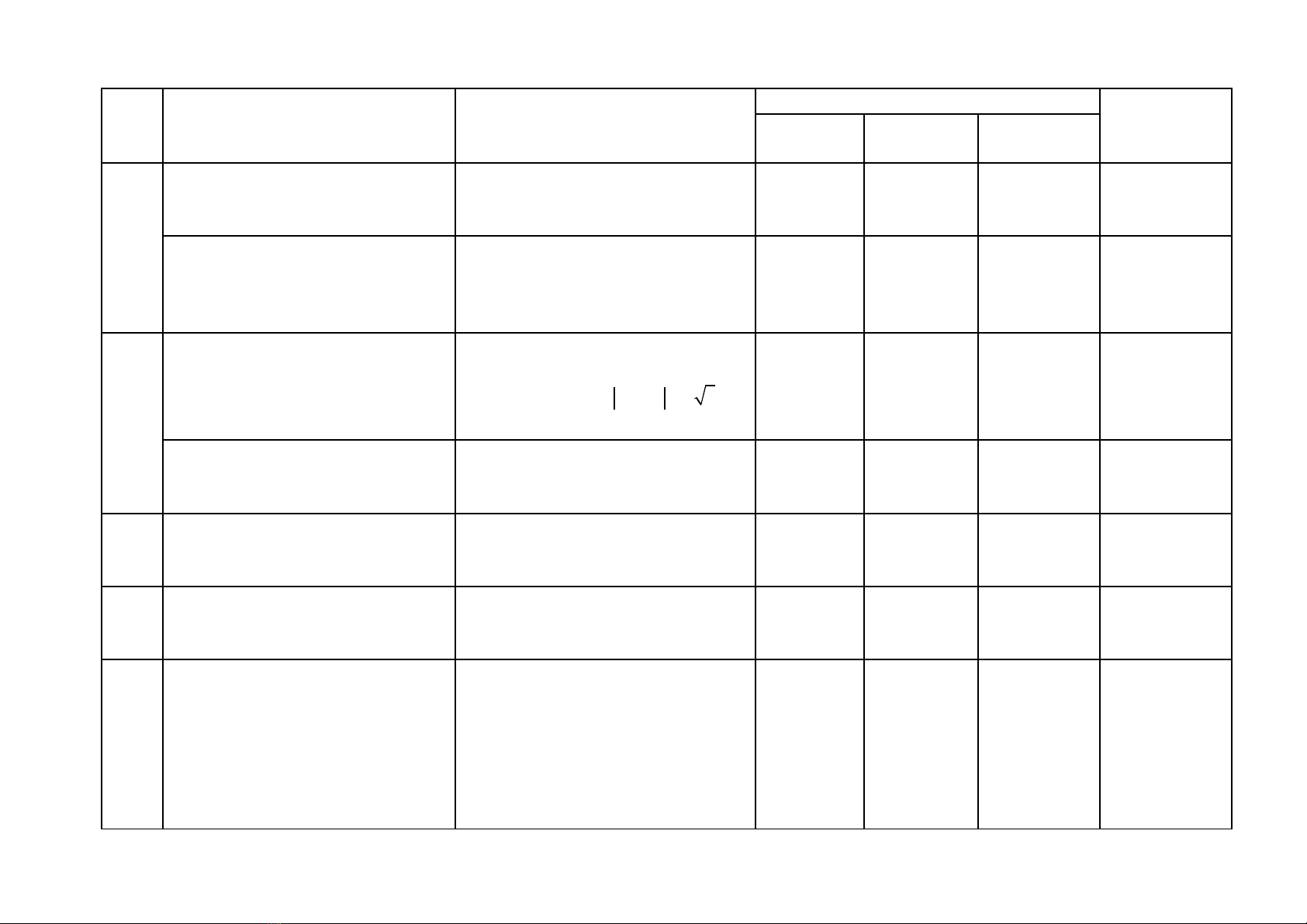
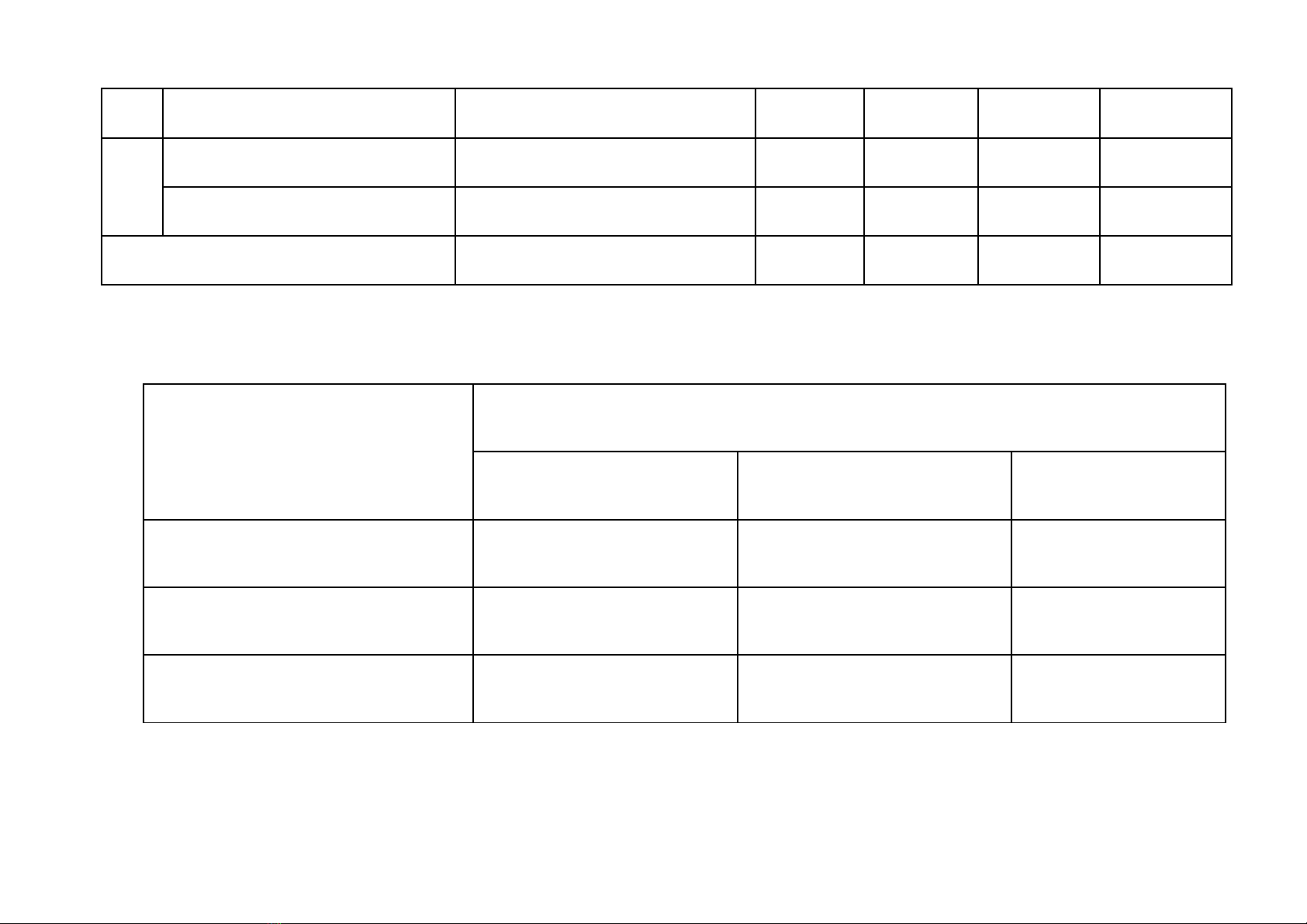
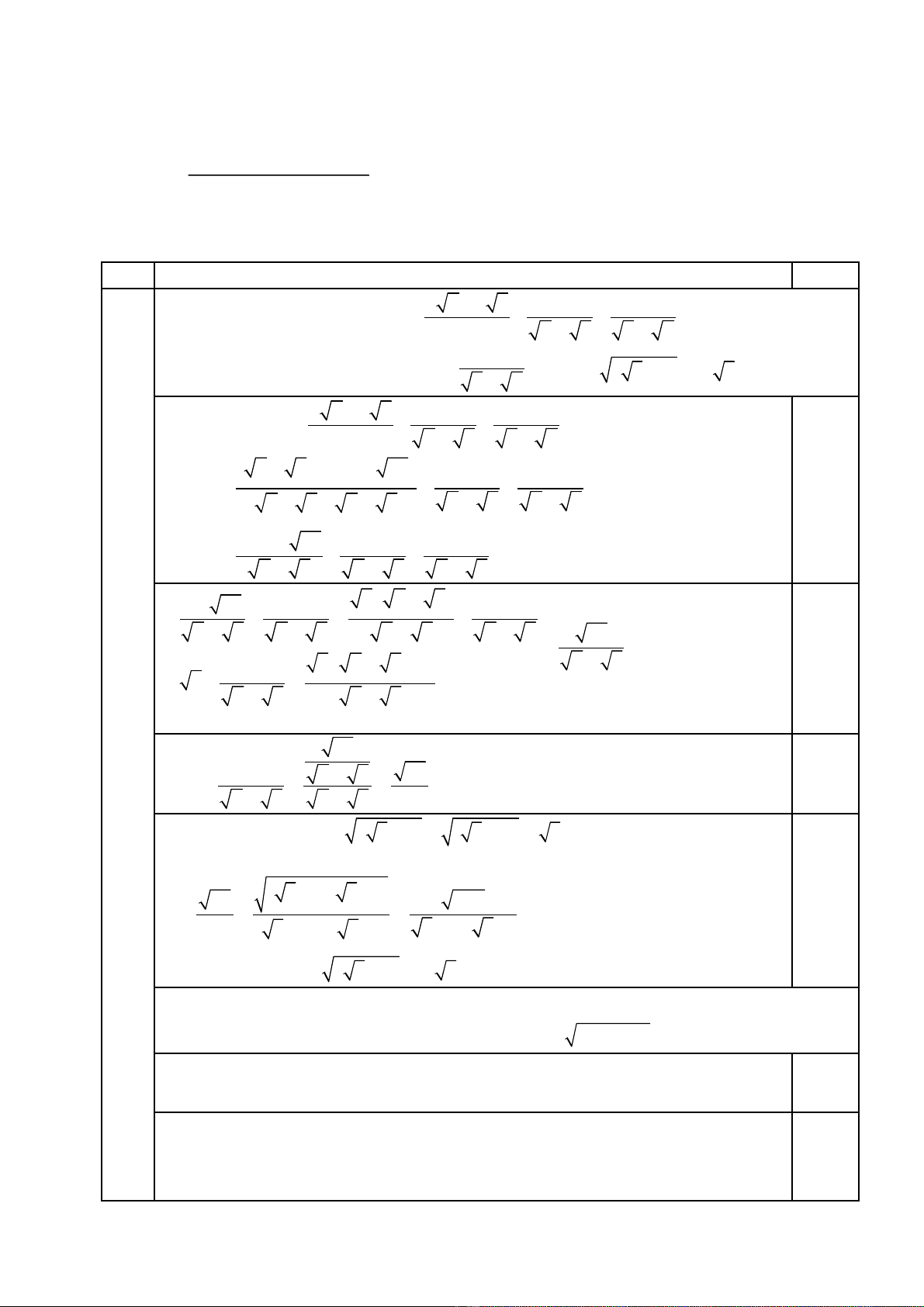
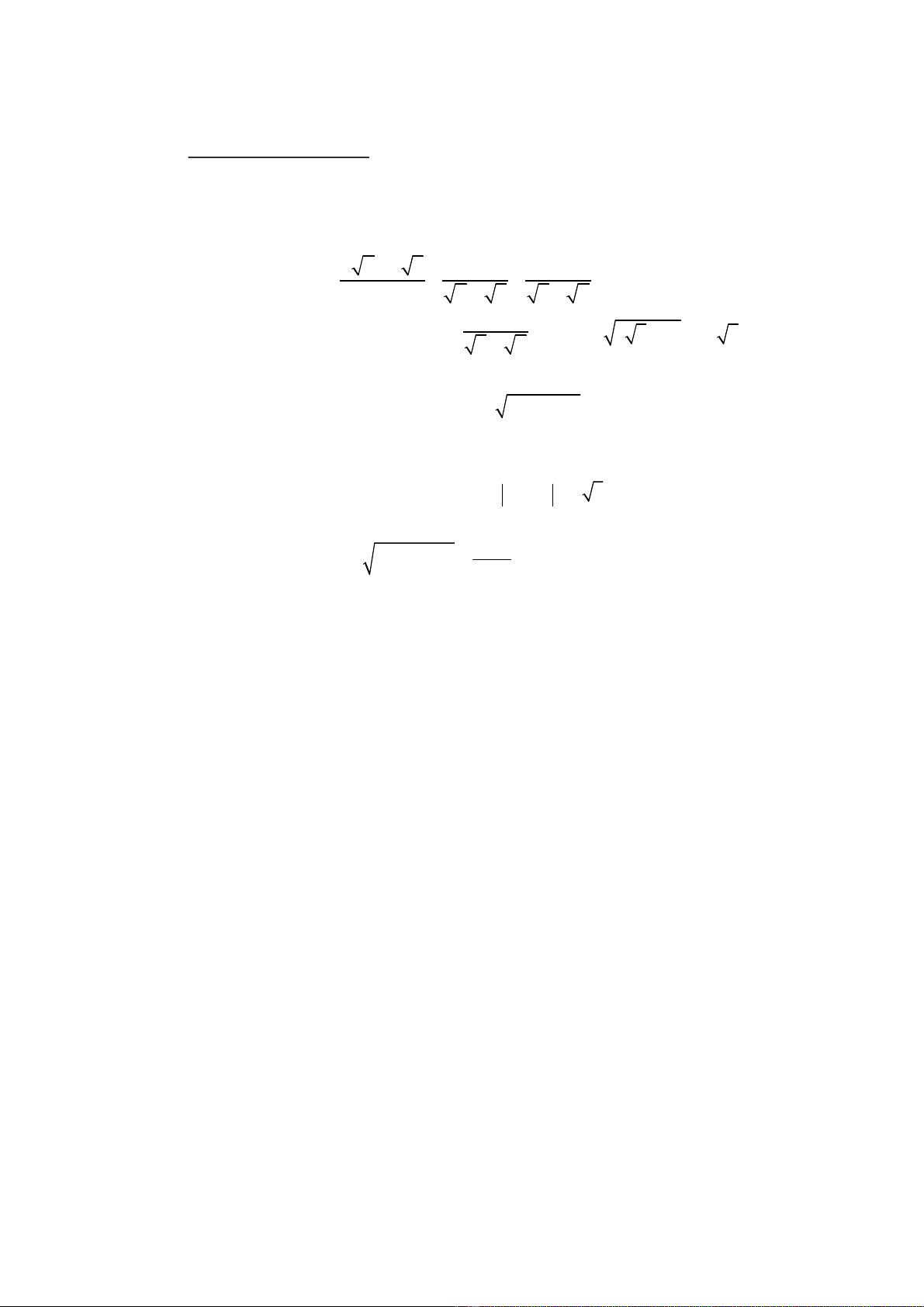TT Nội dung (đơn vị kiến thức) Mức độ kiến thức, kĩ năng
cần đánh giá Số câu hỏi theo mức độ nhận thức Tổng %
Điểm
Thông
hiểu
Vận dụng Vận dụng
cao
1Biến đổi đại số:
a) Rút gọn, tính giá trị biểu thức
Vận dụng được các kiến thức đã
học để rút gọn biểu thức và tính giá
trị của biểu thức
1
1,0đ 1,0đ
10%
b) Giải hệ phương trình. Hiểu được khi giải hệ có phương
trình vô tỉ thì trước tiên cần điều
kiện, biết cách biến đổi hệ cũ về hệ
mới có thêm điều kiện
1
1,0đ 1,0đ
10%
2
Đa thức và bất đẳng thức:
a) Định lý Vi ét
Hiểu được phương trình bậc 2 có hệ
số a khác 0, vận dụng định lý Vi-ét
để chứng minh
1 2
2 3x x
−
với
mọi số
n
nguyên dương
1
1,0đ 1,0đ
10%
b) Bất đẳng thức; tìm giá trị nhỏ
nhất của biểu thức.
HS biết cách đặt ẩn phụ (cho gọn),
biết tìm điểm rơi hợp lý trong định
lý Cô – si để giải quyết bài toán
1
1,0đ 1,0đ
10%
3Số học (02 ý nhỏ):
- Quan hệ chia hết
Vận dụng tính chất chia hết của
tổng, tích…. để chứng minh chia
hết
1
0,75đ 0,75đ
7,5%
- Số chính phương, số lập
phương.
HS sử dụng mối quan hệ giữa chia
hết và số nguyên tố để tìm nghiệm
nguyên
1
0,75đ 0,75đ
7,5%
4Hình học phẳng:
Các phương pháp chứng minh tứ
giác nội tiếp, hai tam giác đồng
dạng, góc với đường tròn
- HS hiểu được cách chứng minh 4
điểm cùng nằm trên 1 đường tròn
- Vận dụng được kiến thức về tiếp
tuyến để chứng minh đường thẳng
là tiếp tuyến của đường tròn
- HS liên kết các kiến thức đã học:
góc với đường tròn, tam giác đồng
1
1,0đ
1
1,0đ
1
1,0đ
3,0đ
30%
dạng để chứng minh đoạn thẳng
bằng nhau
5Tổ hợp (02 ý nhỏ):
- Bài toán đếm.
Biết sử dụng quy tắc nhân để đếm
số
1
0,75đ
0,75đ
7,5%
- Nguyên lí Dirichlet Biết lập dãy số, sử dụng nguyên lý
Dirichlet để chứng minh chia hết
1
0,75đ
0,75đ
7,5%
Tổng 3
2,75đ
4
4,5đ
3
2,75đ
10,0đ
100%
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN
Môn: TOÁN
Năng lực
Cấp độ tư duy
Thông hiểu Vận dụng Vận dụng cao
Tư duy và lập luận Toán học 2
(Câu 3a, 4a)
3
(Câu 1a;2a,3b) 0
Giải quyết vấn đề Toán học 1
(Câu 1b)
3
(Câu 4b,5a,5b)
2
(Câu 2b, 4c)
Tổng
(Số lệnh hỏi của từng cấp độ tư duy) 3 6 2
PHÒNG GD&ĐT HOA LƯ
TRƯỜNG THCS ĐINH TIÊN HOÀNG
ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN
Năm 2024
MÔN: TOÁN
Thời gian làm bài: 150 phút
(Đề thi gồm 05 câu, 01 trang)
Câu 1 (2,0 điểm)
a) Cho biểu thức
a a b b a b
Aa b a b b a
−
= − −
−+ −
với
, 0a b
>
và
a b
Rút gọn và tính giá trị biểu thức
khi
3
a 8 5 16;b 5 1
= − = +
b) Giải hệ phương trình
2 2
2 3 6
3 2 1 2 2 6
x xy y
x y x y
+ + =
+ + = + +
Câu 2 (2,0 điểm)
a) Cho phương trình bậc:
( )
2
2 1 0nx n x n
− + + =
(1) với
n
là tham số. Gọi
1 2
;x x
là 2
nghiệm của phương trình đã cho. Chứng minh rằng
1 2
2 3x x
−
với mọi số
n
nguyên dương.
b) Xét hai số thực
,x y
thay đổi luôn thỏa mãn điều kiện
2x y
+
. Tìm giá trị nhỏ
nhất của biểu thức
( )
4 4
8
4 2 1P x y x y
= + + +
+
Câu 3 (1,5 điểm)
a) Cho x, y là các số nguyên thỏa mãn
3 3 2 2
1+ + + + −x y x y xy
chia hết cho
1.
+ + +
xy x y
Chứng minh rằng
4 9
+
x y
chia hết cho
1.
+
y
b) Tìm tất cả các số nguyên tố
x
và
y
thỏa mãn
4 3
11 .x y
+ =
Câu 4 (3,0 điểm)
Cho tam giác
ABC
có góc
B
tù,
>
AC AB
và nội tiếp đường tròn
( )
O
. Gọi
,M N
lần lượt là trung điểm của
,AB AC
;
D
là chân đường phân giác trong của
ﾷ
BAC
(
D BC
).
a) Chứng minh rằng
, , ,A M N O
cùng thuộc một đường tròn.
b) Gọi
I
là giao điểm của
AD
và
MN
, đường thẳng qua
I
vuông góc với
AD
cắt
BC
tại
S
. Chứng minh rằng tam giác
ASD
cân và
SA
là tiếp tuyến của đường tròn
( )
O
.
c) Gọi
E
là điểm đối xứng với
M
qua
B
, đường tròn ngoại tiếp tam giác
CME
cắt
AC
tại
F
. Đường thẳng
SA
cắt
,FE FM
lần lượt tại
,P Q
. Chứng minh rằng
=AP AQ
.
Câu 5 (1,5 điểm)
a) Có bao nhiêu số tự nhiên có 6 chữ số đôi 1 khác nhau được viết từ 6 chữ số 0; 1; 2;
3; 4; 5 sao cho 2 chữ số 3 và 4 đứng cạnh nhau.
b) Cho 5 số tự nhiên
, , , ,a b c d e
. Chứng minh rằng tồn tại một số chia hết cho 5
hoặc tồn tại một vài số có tổng chia hết cho 5.
------------Hết------------
PHÒNG GD&ĐT HOA LƯ
TRƯỜNG THCS ĐINH TIÊN HOÀNG
HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN
Năm 2024
MÔN: TOÁN
(Hướng dẫn chấm gồm 5 trang)
Câu Đáp án Điểm
1
(2,0
điể
m)
a. (1,0 điểm) Cho biểu thức
a a b b a b
Aa b a b b a
−
= − −
−+ −
với
, 0a b
>
và
a b
Rút gọn và tính giá trị biểu thức
khi
3
a 8 5 16;b 5 1
= − = +
1. Ta có:
a a b b a b
Aa b a b b a
−
= − −
−+ −
( ) ( )
( ) ( )
a b a b ab a b
a b a b
a b a b
a b ab a b
a b a b a b
− + +
= − +
+ −
− +
+ +
= − +
+ + −
0,25
điểm
( )
( )
b a b
b ab b b
a b a b a b a b
b a b b
b
ba b a b
+
+
= + = +
+ − + −
− +
= + =
− −
ab
a b
=−
0,25
điểm
ab
A ab
a b
Ba b
a b a b
−
= = = −
+ +
0,25
điểm
Ta nhận thấy rằng
3
33
8 5 16 ( 5 1) 5 1a
= − = − = −
.Thế
a
và
b
vào
B
, ta
có:
( ) ( )
( ) ( )
5 1 5 1 5 1 1
5 1 5 1
5 1 5 1
ab
Ba b
− + −
= = = = −
−− − −
− − +
.
Vây
1B
= −
khi
3
8 5 16; 5 1a b= − = +
.
0,25
điểm
b. (1,0 điểm) Giải hệ phương trình
2 2
2 3 6
3 2 1 2 2 6
x xy y
x y x y
+ + =
+ + = + +
Điều kiện
: 2 6 0x y
+ +
. Nhân 4 vào phương trình thứ nhất của hệ ta có :
( )
2 2
4 2 3 24 0(2)
+ + − =
x xy y
0,25
điểm
Phương trình thứ hai của hệ tương đương với :
( ) ( )
2
3 2 1 0
3 2 1 4 2 6 0
x y
x y x y
+ +
+ + − + + =
.
0,25
điểm