S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
QU NG NAMẢK THI TUY N SINH L P 10 THPT CHUYÊNỲ Ể Ớ
NĂM H C 2019-2020Ọ
ĐÊ CHINH TH C ƯMôn thi : TOÁN (Toán chuyên)
Th i gianờ: 150 phút (không k th i gian giao để ờ ề)
Khóa thi ngày: 10-12/6/2019
Câu 1 (2,0 đi mể).
a) Cho bi u th c v i ể ứ ớ
Rút g n bi u th c và tìm đ ọ ể ứ ể
b) Ch ng minhứ r ng v i m iằ ớ ọ s nguyên d ng , s chia h t cho 20.ố ươ ố ế
Câu 2 (1,0 đi mể).
Cho parabol va đng thăng Tim t t c các giá tr c a tham s đê căt tai hai điêm ươ ấ ả ị ủ ố
phân biêt l n l t có hoành đ th a mãn ầ ượ ộ ỏ
Câu 3 (2,0 đi mể).
a) Gi i ph ng trình ả ươ
b) Giai hê ph ng trinh ươ
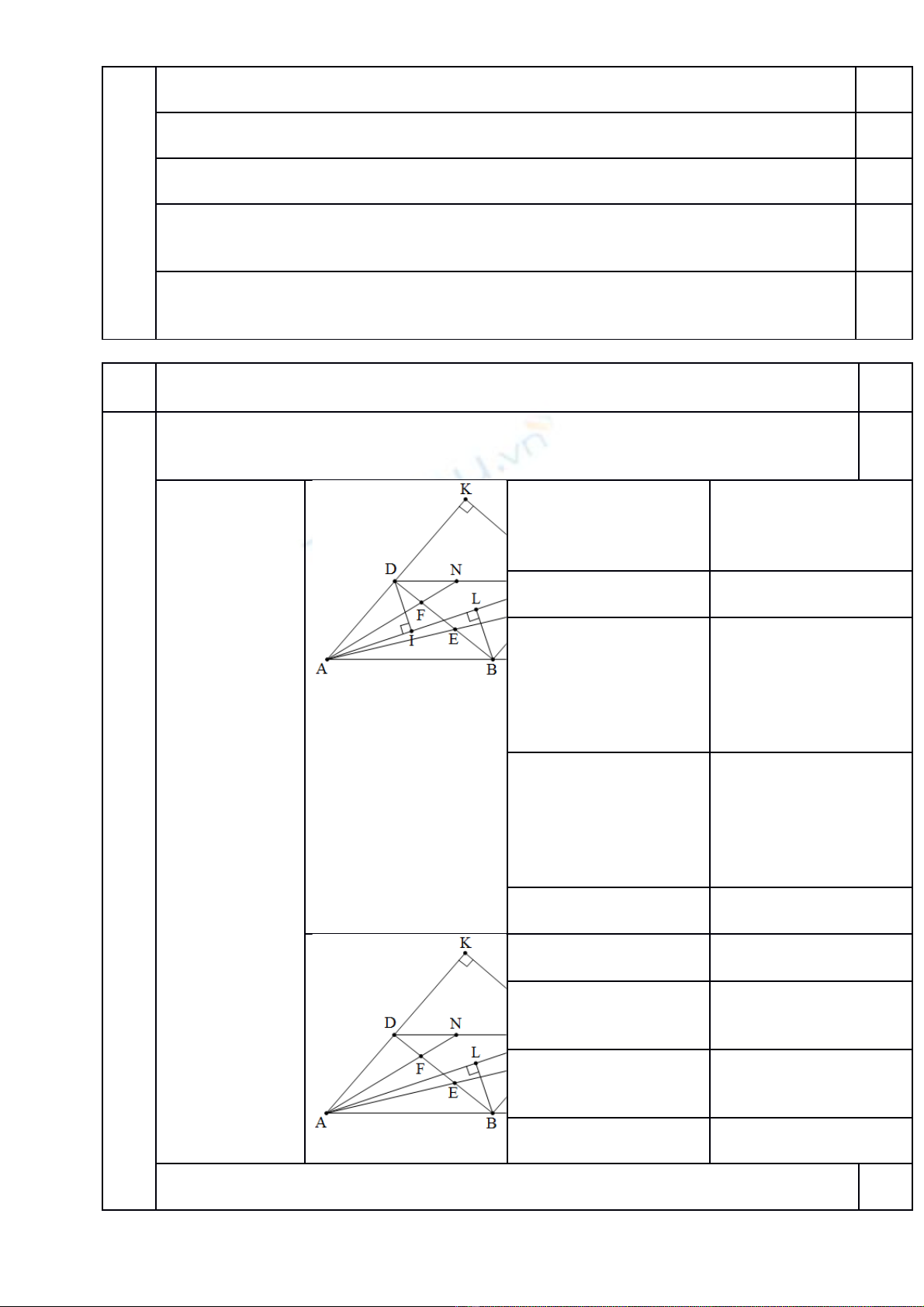
Câu 4 (2,0 đi mể).
Cho hinh bình hành có góc nh n. G i l n l t là hình chi u vuông góc c a lên cácọ ọ ầ ượ ế ủ
đng thăng ươ
a) Ch ng minh ư
b) Trên hai đo n th ng l n l t l y hai đi m ( khác khác ) sao cho ạ ẳ ầ ượ ấ ể hai tam giác
và có di n tíchệ b ng nhau;ằ c tắ và l n l t t i và Ch ng minh ầ ượ ạ ứ và
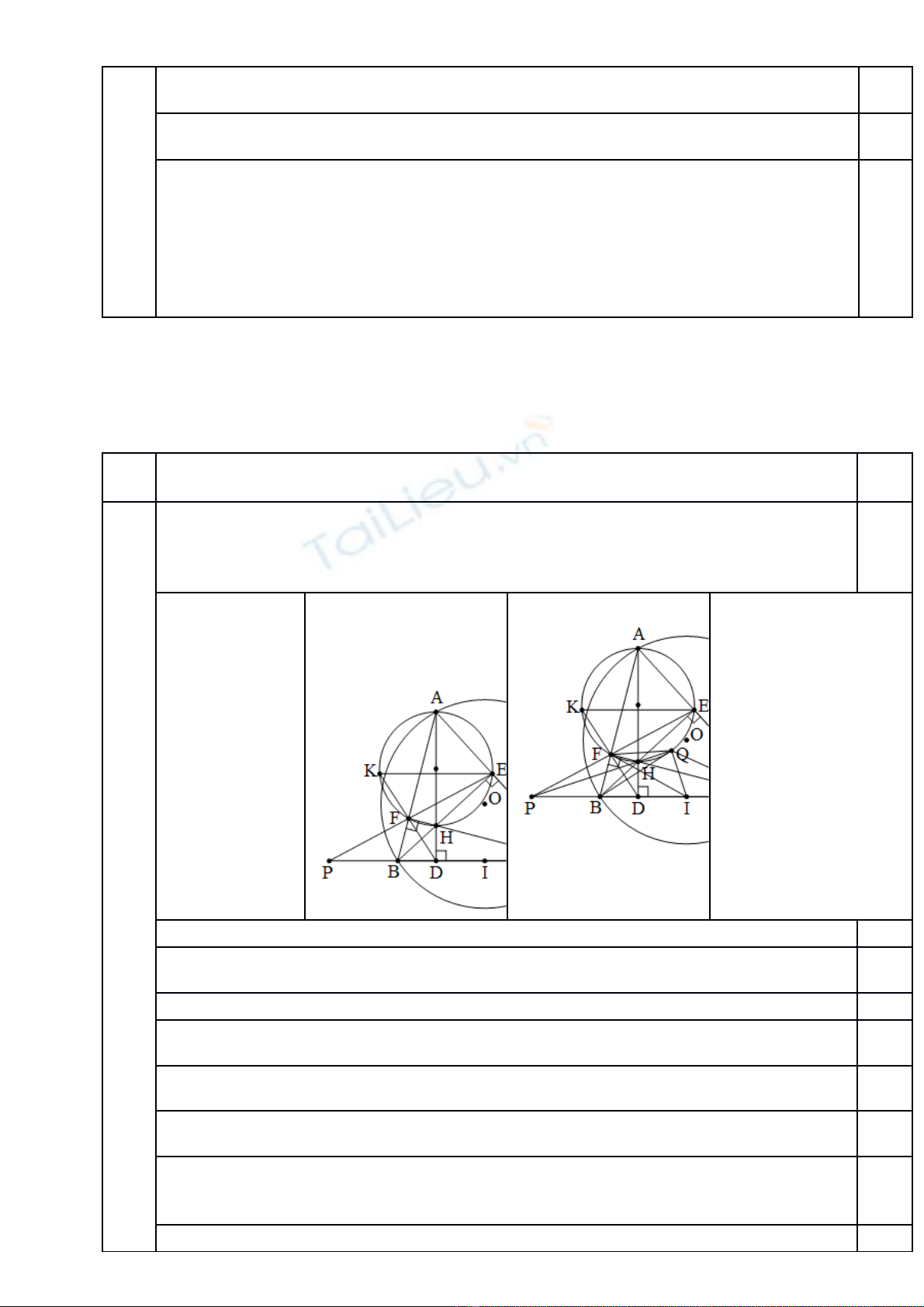
Câu 5 (2,0 đi mể).
Cho tam giác nh n n i ti p đng tròn và có tr c tâm Ba đi m l n l t làọ ộ ế ườ ự ể ầ ượ
chân các đng cao v t c a tam giác G i là trung đi m c a c nh là giao đi m c a vàườ ẽ ừ ủ ọ ể ủ ạ ể ủ
Đng th ng c t đng tròn ngo i ti p tam giác t i đi m th hai là ườ ẳ ắ ườ ạ ế ạ ể ứ
a) Ch ng minh và song song v i ứ ớ
b) Đng th ng c t đng tròn ngo i ti p tam giác t i đi m th hai là Ch ngườ ẳ ắ ườ ạ ế ạ ể ứ ứ
minh t giác n i ti p đng trònứ ộ ế ườ .
Câu 6 (1,0 đi mể).
Cho ba s th c d ng ố ự ươ thoa mãn Tim gia tri nh nhât cua biêu th c ỏ ư
--------------- H TẾ ---------------
H và tên thí sinh:ọ ........................................................................................ S báo danh:ố
......................................
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
QU NG NAMẢK THI TUY N SINH L P 10 THPT CHUYÊNỲ Ể Ớ
NĂM H C 2019-2020Ọ
HDC CHINH TH C ƯH NG D N CH M MÔN TOÁN CHUYÊNƯỚ Ẫ Ấ
(B n h ng d n này g m 05 trang)ả ướ ẫ ồ
Câu N i dungộĐiể
m
Câu a) Cho bi u th c v i .ể ứ ớ
Rút g n bi u th c và tìm đ .ọ ể ứ ể 1,25