S GIÁO D C VÀ ĐÀOỞ Ụ
T OẠ
QU NG NAMẢ
K THI TUY N SINH L P 10 THPT CHUYÊNỲ Ể Ớ
NĂM H C Ọ2019 - 2020
ĐÊ CHINH TH C Ư
(Đ có 01 trangề)
Môn thi: TOÁN (chuyên Tin)
Th i gian:ờ 150 phút (không k th i gian giao để ờ ề)
Khóa thi ngày: 10 - 12/6/2019
Câu 1 (1,5 đi mể).
Cho bi u th c v i và . ể ứ ớ
Rút g n bi u th c và tìm đ ọ ể ứ ể
Câu 2 (1,0 đi mể).
Tìm t t c các c p s t nhiên th a mãn ấ ả ặ ố ự ỏ
Câu 3 (2,0 đi mể).
a) Gi i ph ng trình ả ươ
b) Giai hê ph ng trinh ươ
Câu 4 (1,0 đi mể).
Cho parabol và đng thăng (là tham s ). Tìm đ căt tai hai điêm phân biêt A, B ươ ố ể sao
cho tam giác OAB đu (v i O là g c t a đ).ề ớ ố ọ ộ
Câu 5 (3,5 đi mể).
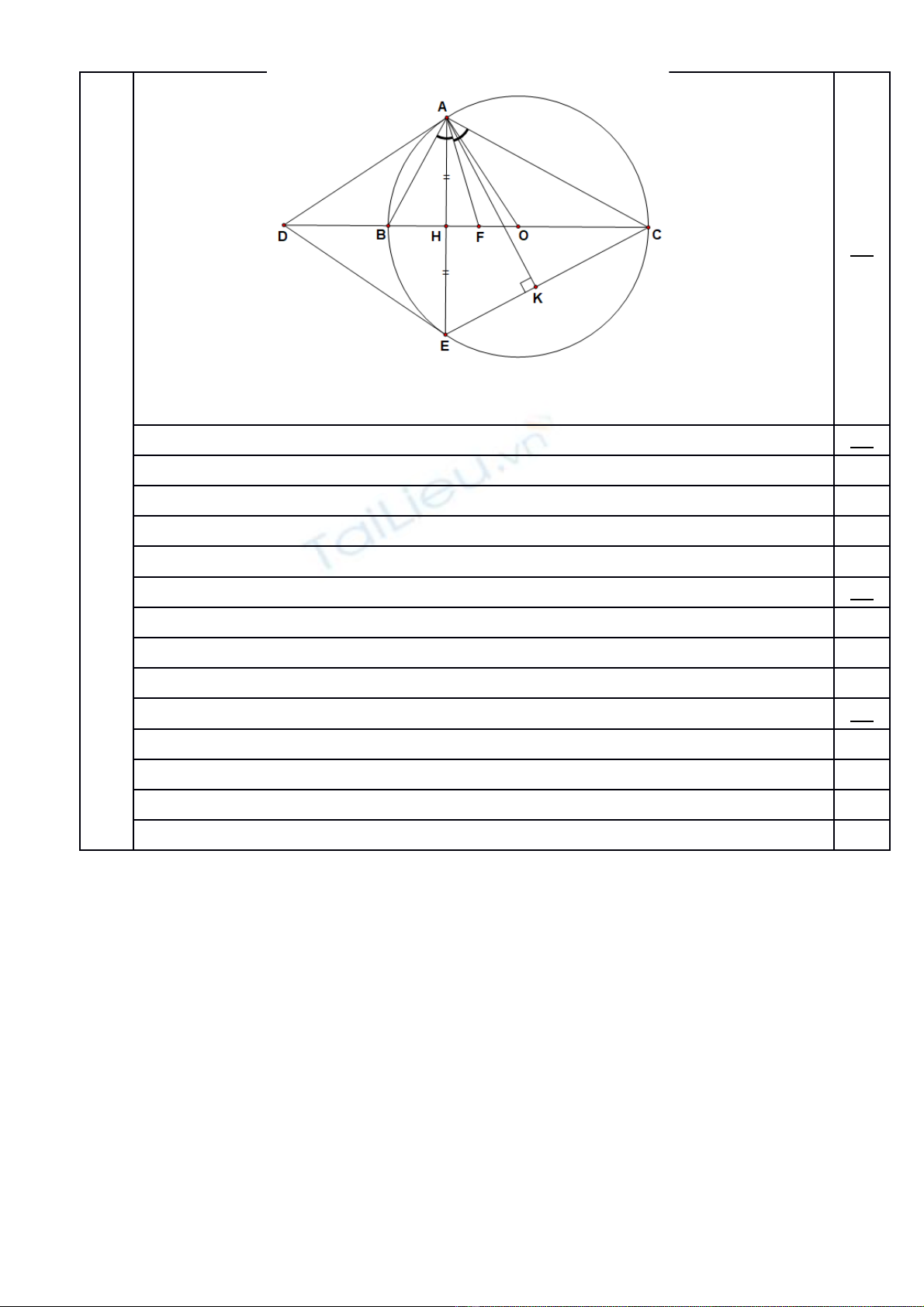
Cho tam giác ABC (AB < AC) n i ti p đng tròn (O) đng kính BC, ti p tuy n c aộ ế ườ ườ ế ế ủ
đng tròn (O) t i A c t đng th ng BC t i D. V dây cung AE c a đng tròn (O) vuôngườ ạ ắ ườ ẳ ạ ẽ ủ ườ
góc v i BC. G i H là giao đi m c a AE và BC, K là hình chi u vuông góc c a A lên CE. ớ ọ ể ủ ế ủ Tia
phân giác c a c t BC t i F. ủ ắ ạ
a) Ch ng minh AB.HC = AC.HA.ứ
b) Ch ng minh .ứ
c) Ch ng minh .ứ
Câu 6 (1,0 đi mể).
Cho ba s th c d ng ố ự ươ Tìm giá tr l n nh t c a bi u th c ị ớ ấ ủ ể ứ
--------------- H TẾ ---------------
H và tên thí sinhọ: .................................................................. S báo danhố: ...........................
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
QU NG NAMẢK THI TUY N SINH L P 10 THPT CHUYÊNỲ Ể Ớ
NĂM H C 2019-2020Ọ
HDC CHINH TH C ƯH NG D N CH M MÔN: TOÁN (Chuyên Tin)ƯỚ Ẫ Ấ
(B n h ng d n này g m 04 trang)ả ướ ẫ ồ
Câu N i dungộĐiể
m
Câu
1
(1,5)
Cho bi u th c , v i và . Rút g n bi u th c và tìm đ ể ứ ớ ọ ể ứ ể 1,5
(Đúng m i ý đc 0,25đỗ ượ )0,5
(đúng 2 ý sau, m i ý đc 0,25đỗ ượ )0,5
.0,25
- Đi chi u đi u ki n suy ra là giá tr c n tìm.ố ế ề ệ ị ầ 0,25
Câu N i dungộĐiể
m
Câu
2
(1,0)
Tìm t t c các c p s t nhiên th a mãn ấ ả ặ ố ự ỏ 1,0
(1) 0,25
* và là hai s cùng ch n, cùng l và . Do đó t (1) ta có:ố ẵ ẻ ừ
( v i là hai s t nhiên và ).ớ ố ự
(2) 0,25
Suy ra: . 0,25
Khi đó
V y ậ0,25
Câu N i dungộĐiể
m
Câu
3
(2,0)
a) Gi i ph ng trình ả ươ 1,0
(N u h c sinh ch ghi đc đi u thì cho 0,25ế ọ ỉ ượ ề )0,25
0,25
0,25
(th a đi u ki n)ỏ ề ệ
V y ph ng trình đã cho có m t nghi m .ậ ươ ộ ệ 0,25
b) Giai hê ph ng trinh ươ 1,0
(*) 0,25
Đt . Khi đó h (*) tr thành: ặ ệ ở
ho c ặ0,25
V i ớ0,25
V i ho c .ớ ặ 0,25
Câu N i dungộĐiể
m
Câu
4
(1,0)
Cho parabol và đng thăng (là tham s ). Tìm đ căt tai hai điêm phân biêt ươ ố ể sao cho
tam giác đu (v i là g c t a đ).ề ớ ố ọ ộ 1,0
+ Ph ng trình hoành đ giao đi m c a (P) và (d) là:ươ ộ ể ủ .
+ Đ (d) c t (P) t i hai đi m phân bi t thì ể ắ ạ ể ệ 0,25
V i đi u ki n trên, ta có:. Khi đó ta có: ớ ề ệ 0,25
G i H là trung đi m c a AB.ọ ể ủ
Tam giác OAB cân t i O, do đó tam giác OAB đu khi:ạ ề 0,25
(vì ).
V y là giá tr c n tìm.ậ ị ầ 0,25
Câu N i dungộĐiể
m
Câu
5
(3,5)
Cho tam giác ABC (AB < AC) n i ti p đng tròn (O) đng kính BC, ti p tuy n c aộ ế ườ ườ ế ế ủ
đng tròn (O) t i A c t đng th ng BC t i D. V dây cung AE c a đng tròn (O)ườ ạ ắ ườ ẳ ạ ẽ ủ ườ
vuông góc v i BC. G i H là giao đi m c a AE và BC, K là hình chi u vuông góc c a Aớ ọ ể ủ ế ủ
lên CE. Tia phân giác c a c t BC t i F. ủ ắ ạ
a) Ch ng minh AB.HC = AC.HA.ứ
b) Ch ng minh .ứ
c) Ch ng minh .ứ
Hình v ph c câu b: ẽ ụ 0,25
Hình v ph c c hai câu b và c: ẽ ụ ả 0,25
0,5
a) Ch ng minh ứAB.HC = AC.HA.1,0
Xét hai tam giác và có: , 0,25
. Suy ra hai tam giác và đng d ng. ồ ạ 0,25
Do đó 0,25
.0,25
b) Ch ng minhứ 1,0
(đúng m i ý đc 0,25ỗ ượ )0,5
+ L p lu n đc tam giác ADE cân t i D nên ậ ậ ượ ạ 0,25
Suy ra 0,25
c) Ch ng minh .ứ1,0
(cùng ch n cung ), (vì là phân giác c a )ắ ủ 0,25
Suy ra: . Suy ra tam giác ADF cân t i D.ạ0,25
+ Ch ng minh đc hai tam giác và đng d ng. ứ ượ ồ ạ 0,25
Suy ra . H n n a nên ơ ữ 0,25
Câu N i dungộĐiể
m
Câu
6
(1,0)
Cho ba s th c d ng ố ự ươ Tìm giá tr l n nh t c a bi u th c ị ớ ấ ủ ể ứ
.1,0
0,25
0,25
0,25
T ng t : .ươ ự
Suy ra (d u ‘‘=’’ x y ra khi ).ấ ả
V y giá tr l n nh t c a ậ ị ớ ấ ủ A b ng 1 khi .ằ0,25
--------------- H TẾ ---------------
* L u ý:ư N u thí sinh làm bài không theo cách nêu trong đáp án nh ng đúng thì v n cho đ s đi mế ư ẫ ủ ố ể
t ng ph n nh h ng d n quy đnh.ừ ầ ư ướ ẫ ị