ĐỀ TUYỂN SINH VÀO LỚP 10 CHUYÊN
MÔN TOÁN - NĂM 2024
(ĐỀ 1_Toan_PG3_TS10C_2024_DE_SO_3.doc)
I. MA TRẬN ĐỀ
TT Nội dung kiến thức
Mức độ nhận thức Tổng Tỉ lệ
%
tổng
điểm
Thông hiểu Vận dụng Vận dụng cao
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
1
Biến đổi biểu thức nhiều
biến có điều kiện liên hệ
giữa các biến
1 1 10 1 1 10 10%
2Hệ phương trình 1 1 15 1 1 15 10%
3Đa thức 1 1 15 1 1 15 10%
4Bất đẳng thức 1 1 20 1 1 20 10%
5Số học 1 0,75 10 1 0,75 15 2 1,5 25 15%
6Hình học phẳng 1 1 10 1 0,75 10 1 1,25 20 3 3 40 30%
7Tổ hợp 2 1,5 25 25 15%
II. BẢNG ĐẶC TẢ
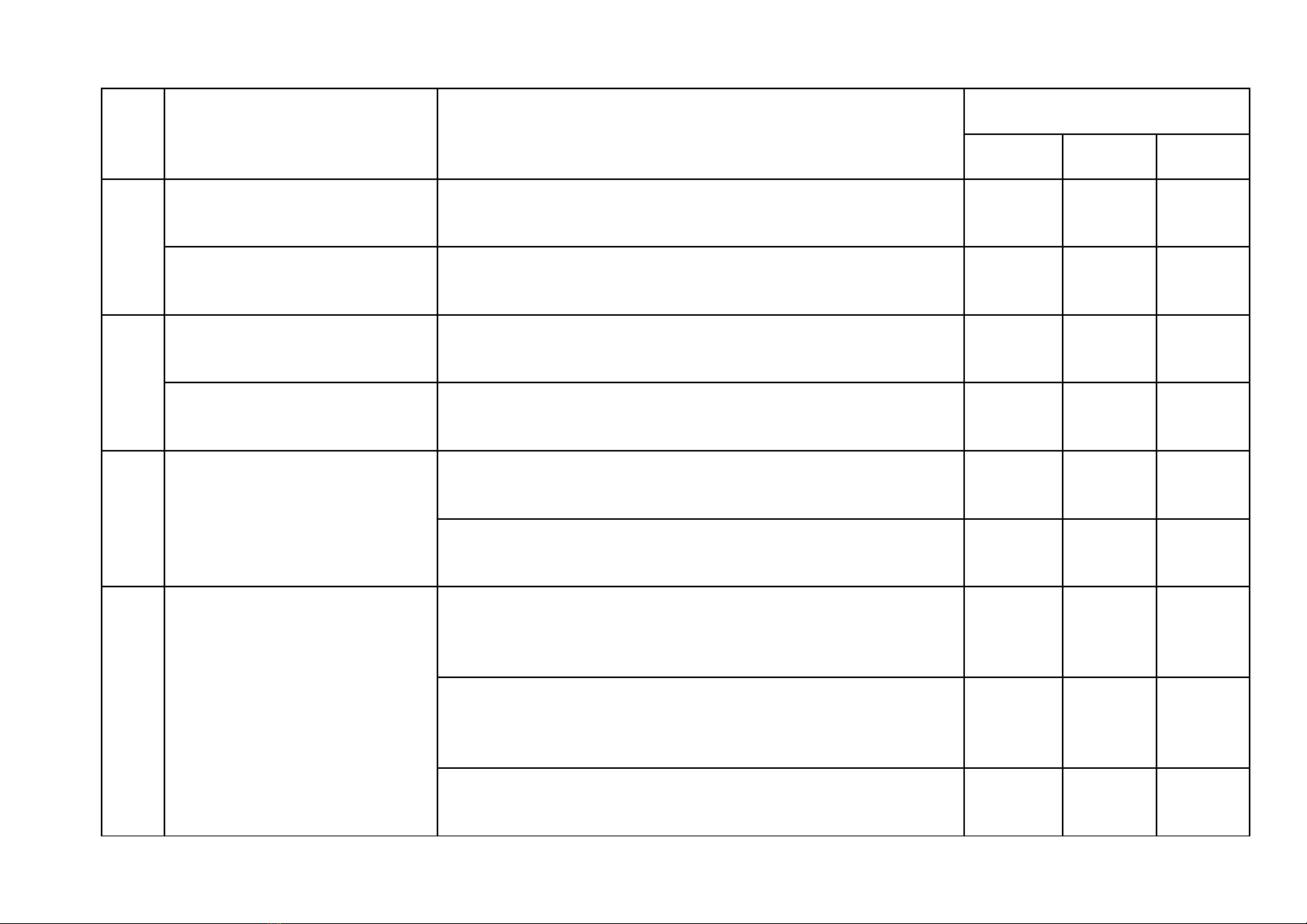
STT Tên chủ đề/
Nội dung
Mức độ kiến thức, kĩ năng
cần đánh giá
Số câu hỏi
theo mức độ nhận thức
Thông
hiểu
Vận
dụng VD cao
1 Biến đổi đại số
Câu 1(2,0 điểm)
Thông hiểu:
- Biến đổi được hệ thức ràng buộc giữa các biến để tính được giá trị
của biểu thức.
1
(câu 1.1)
Vận dụng:
- Biết sử dụng các PP giải HPT để giải hệ phương trình 2 ẩn bằng
cách đưa về giải phương trình bậc hai 1 ẩn.
1
(câu 1.2).
2 Đa thức và bất đẳng thức.
Câu 2 (2,0 điểm)
Thông hiểu:
Giải được bài toán về giá trị đa thức có điều kiện ràng buộc giữa các
biến.
1
(câu 2.1)
Vận dụng cao:
Biết sử dụng bất đẳngthức Cauchy-Schwarz để chứng minh bất
đẳng thức từ đó tìm được giá trị nhỏ nhất của một biểu thức.
1
(câu 2.2)
3Chia hết và nghiệm nguyên
Câu 3 (1,5 điểm)
Vận dụng:
- Biết sử dụng dấu hiệu, tính chất chia hết để tìm được số mũ trong
lũy thừa.
1
(câu 3.1)
Vận dụng cao:
- Biết sử dụng tính chất chia hết để tìm nghiệm nguyên của phương
trình 2 ẩn.
1
(câu 3.2)
4 Hình học
Câu 4 (3,0 điểm)
Thông hiểu:
- Biết sử dụng dấu hiệu nhận biết và tính chất của tứ giác nội tiếp để
chứng minh một tứ giác là TGNT và chứng minh được hai tam giác
đồng dạng suy ra hệ thức về các cạnh tương ứng của chúng.
1
(câu 4a)
Vận dụng:
- Biết chứng minh ba điểm thẳng hàng, đường trung bình của tam
giác để suy ra quan hệ về độ dài giữa 2 đoạn thẳng và tính được tỉ
số của chúng.
1
(câu 4b)
Vận dụng cao:
- Biết sử dụng dấu hiệu nhận biết và tính chất của tứ giác nội tiếp để
tìm ra các TGNT và các góc bằng nhau, từ đó suy ra các tam giác
1
(câu 4c)
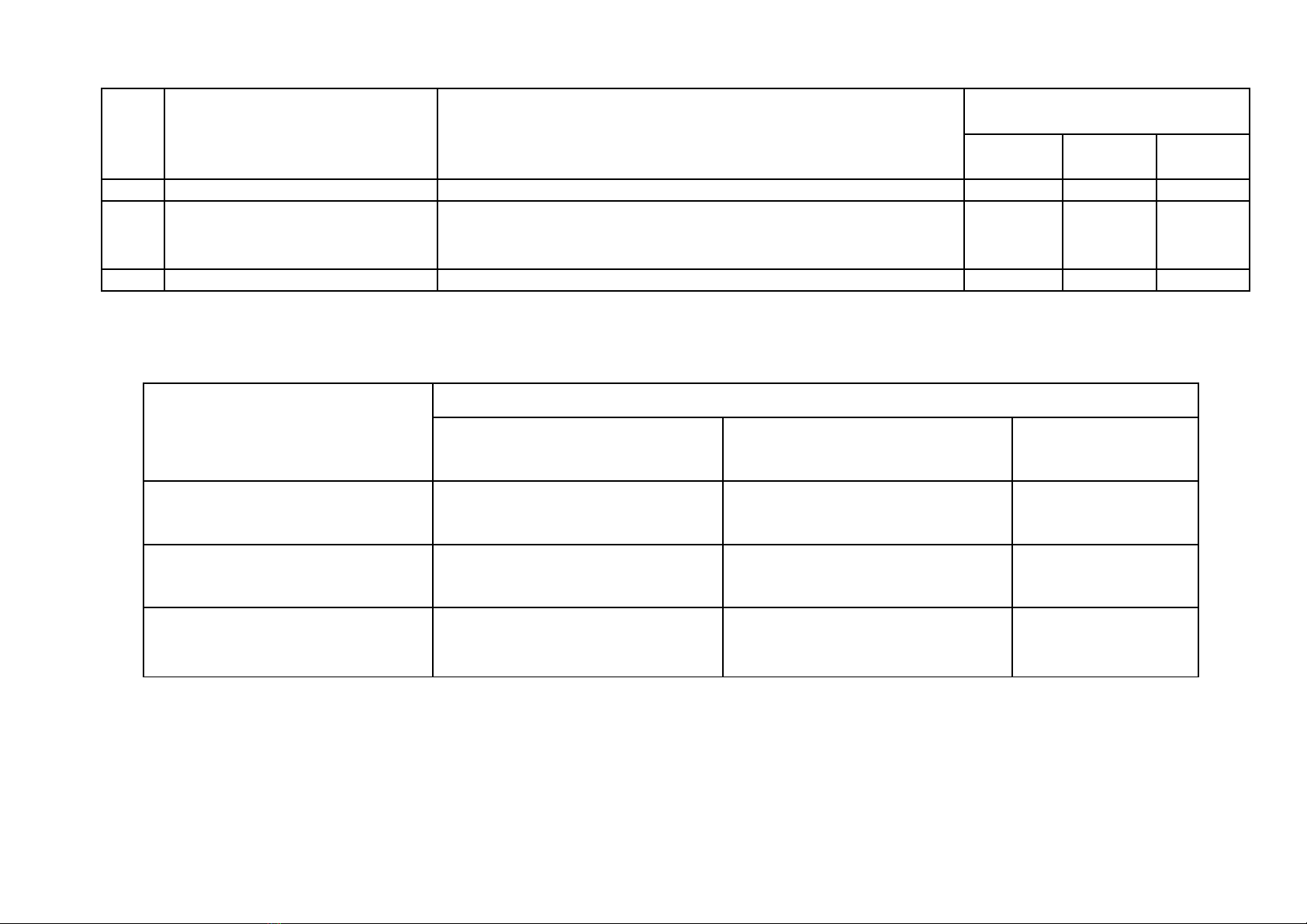
STT Tên chủ đề/
Nội dung
Mức độ kiến thức, kĩ năng
cần đánh giá
Số câu hỏi
theo mức độ nhận thức
Thông
hiểu
Vận
dụng VD cao
đồng dạng để chứng minh 3 điểm thẳng hàng.
5 Tổ hợp
Câu 5 (1,5 điểm)
Vận dụng:
- Đại lượng bất biến, trò chơi.
- Nguyên lí Dirichlet, nguyên lí cực trị.
2
(câu 5.1;
5.2)
Tỉ lệ chung 30,0% 40,0% 30,0%
III. BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY
Năng lực
Cấp độ tư duy
Thông hiểu Vận dụng Vận dụng cao
Tư duy và lập luận Toán học 2
(Câu 1.1, 4a)
1
(Câu 1.2)
1
(Câu 3.2)
Giải quyết vấn đề Toán học 1
(Câu 3.1)
4
(Câu 2.1, 4b, 5.1, 5.2)
2
(Câu 2.2, 4c)
Tổng
(Số lệnh hỏi của từng cấp độ tư
duy)
3 5 3
PHÒNG GD&ĐT HOA LƯ
TRƯỜNG THCS NINH GIANG
ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN
Năm 2024
MÔN: TOÁN
Thời gian làm bài: 150 phút
Đề thi gồm 05 câu, 01 trang
Câu 1 (2,0 điểm).
1. Cho hai số thực x, y thỏa mãn
()()
2 2
x x 1 y y 1 1+ + + + =
.
Tính giá trị biểu thức
2025 2025
A x y= +
.
2. Giải hệ phương trình:
x y xy 3
x 1 y 1 4
+ − =
+ + + =
Câu 2 (2,0 điểm).
1. Cho đa thức
3 2
P(x) 2x 3x 4x 1= − + −
.
a) Chứng minh rằng với hai số thực a, b thoả mãn
a b 1
+ =
thì
.
b) Tính tổng:
1 2 3 2024
S P P P ... P
2025 2025 2025 2025
= + + + +
.
2. Cho các số thực dương a, b, c thỏa mãn
a b c 4050+ + =
. Tìm giá trị nhỏ nhất của biểu
thức:
2 2 2
a b c
Pb c a c b a
= + +
+ + +
.
Câu 3 (1,5 điểm).
1. Tìm các số tự nhiên x, y biết
( ) ( ) ( ) ( )
x x x x y
2 1 2 2 2 3 2 4 5 11879+ + + + − =
2. Tìm nghiệm nguyên của phương trình:
2 2
2x 3y 4x 19+ + =
Câu 4 (3,0 điểm).
Cho
ABC
∆
nhọn
(AB AC)<
nội tiếp đường tròn
(O)
. Hai đường cao BE, CF cắt nhau tại
H. Gọi M là trung điểm của đoạn thẳng BC. Gọi K là giao điểm của hai đường thẳng EF và BC.
a) Chứng minh tứ giác BEFC nội tiếp, từ đó suy ra
KF.KE KB.KC=
b) Tính tỉ số
OM
AH
c) Đường thẳng AK cắt đường tròn (O) tại điểm thứ hai là I (I khác A). Chứng minh ba điểm
M, H, I thẳng hàng
Câu 5 (1,5 điểm).
1. Tổng số bi đỏ và bi xanh trong 4 hộp là 48 viên. Biết rằng trong hộp thứ nhất số bi đỏ và
số bi xanh bằng nhau, trong hộp thứ hai số bi đỏ gấp 2 lần số bi xanh, trong hộp thứ ba số bi đỏ gấp
3 lần số bi xanh, trong hộp thứ tư số bi đỏ gấp 6 lần số bi xanh. Trong 4 hộp này có một hộp chứa 2
viên bi xanh, có một hộp chứa 3 viên bi xanh, có một hộp chứa 4 viên bi xanh, có một hộp chứa 5
viên bi xanh. Tìm số bi đỏ và bi xanh của mỗi hộp.
2. Trên bàn cờ vua có 8x8 ô, người ta viết vào mỗi ô một số từ một đến 64 (không có số nào
được viết 2 lần). Chứng minh rằng luôn tìm được 1 ô trắng và một ô đen mà hiệu 2 số được ghi
trên đó không nhỏ hơn 31.
---------- Hết ----------
1
PHÒNG GD&ĐT HOA LƯ
TRƯỜNG THCS NINH GIANG
HƯỚNG DẪN CHẤM
ĐỀ TUYỂN SINH LỚP 10 CHUYÊN
Năm 2024
MÔN: TOÁN
(Hướng dẫn chấm gồm 05 trang)
Chú ý:
+ Học sinh làm đúng bằng cách nào cũng cho điểm tối đa.
+ Bài làm sai từ đâu phần tiếp theo có liên quan không chấm.
+ Hình vẽ sai hoặc không khớp lời chứng minh thì không chấm.
Câu Đáp án Điểm
1
(2,0
điểm)
1. (1,0 điểm)
Chỉ ra
2 2 2
x 1 x x x x x 1 0+ > = − +
Nhân 2 vế của (*) với
2
x x 1− +
ta được:
()()()()
2 2 2 2
x x 1 x x 1 y y 1 1. x x 1− + + + + + = − +
( )
()()
2 2 2 2
x x 1 y y 1 x x 1
− + + + = − +
2 2
y y 1 x x 1 + + = − + +
(1)
0,25
Tương tự có
2
y y 1 0− +
Nhân 2 vế của (*) với
2
y y 1− +
ta được
2 2
x x 1 y y 1+ + = − + +
(2) 0,25
Cộng theo vế (1) và (2), ta có
2 2 2 2
x x 1 y y 1 y y 1 x x 1+ + + + + = − + + − + +
( )
2 x y 0 + =
x y = −
0,25
Khi đó
( )
2025 2025 2025 2025
A y y y y 0= − + = − + =
0,25
2. (1,0 điểm).
ĐK:
x 1; y 1; xy 0 − −
Đặt
xy t 0=
ta có
2
xy t=
Từ (1) có
x y 3 t+ = +
Từ (2) có
( )
x y 2 2 xy x y 1 16 3
+ + + + + + =
0,25
Thay
x y 3 t+ = +
và
2
xy t=
vào (3) có :
2 2
3 t 2 2 t 3 t 1 16 2 t t 4 11 t
+ + + + + + = + + = −
0,25
( )
( )
2
2
0 t 11
4 t t 4 11 t
+ + = −
Hay
( )
2
0 t 11 4
3t 26t 105 0
+ − =
Giải (4) được
t 3=
thỏa mãn
0,25
Suy ra
x y 6; xy 9 + = =
Từ đó tìm được nghiệm của hệ phương trình là
( ) ( )
x ; y 3 ;3=
.0,25
1. (1,0 điểm).