ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2019 - 2020
MÔN THI: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
-----------------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐIỆN BIÊN
---------------
ĐỀ THI CHÍNH THỨC
ĐỀ BÀI
Câu 1. (2,5 ñim)
Cho biu th$c:
5
3
x
Ax
+
=−
và
1 7 3
9
3
x x
Bx
x
− −
= + −
+
1. Tính A khi x = 25.
2. Rút g6n biu th$c B.
3. Tìm giá tr: nh; nh<t c=a
A
B
.
Câu 2. (2,5 ñim)
1. Gi?i phương trình:
a)
2
5 4 0x x− + = b)
4 2
6 0x x+ − =
2. Gi?i hF phương trình: 2 7
2 1
x y
x y
− =
− =−
Câu 3. (1,0 ñim)
Cho phương trình:
2
1 0x ax b+ + + = (a, b là các tham sI). Tìm a, b ñ phương trình có 2 nghiFm x1, x2 th;a
mãn: 1 2
3 3
1 2
3
9
x x
x x
− =
− =
Câu 4. (3,0 ñim)
Cho t$ giác ABCD nLi tiMp (O; R) và có hai ñưOng chéo AC, BD vuông góc vRi nhau tSi I (I khác O). KU
ñưOng kính CE.
1. Ch$ng minh t$ giác ABDE là hình thang cân.
2. Ch$ng minh:
2 2 2 2
2 2 .AB CD BC AD R+ + + =
3. TX A, B kU các ñưOng thYng vuông góc vRi CD lZn lư[t c\t BD, AC tSi F và K. T$ giác ABKF là hình
gì?
Câu 5. (1,0 ñim)
1. Tìm nghiFm nguyên c=a phương trình:
3 3 2
1.y x x x= + + +
2. Cho các sI nguyên a, b, c th;a mãn ab + bc + ca = 1. Ch$ng minh rbng: A =
( )( )( )
2 2 2
1 1 1a b c+ + + là
mLt sI chính phương.
---------- HẾT ----------
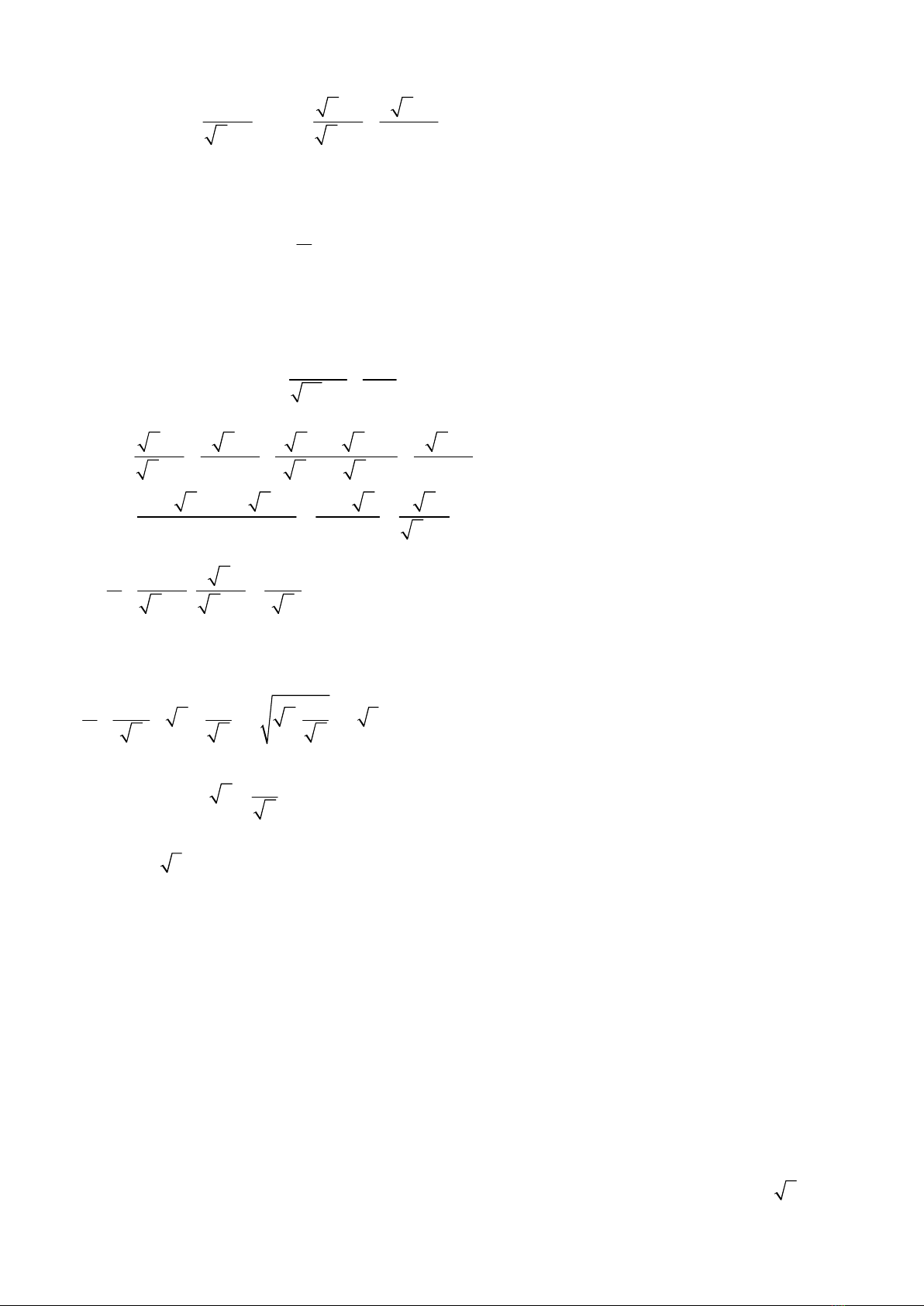
Câu 1. (2,5 ñim)
Cho biu th$c:
5
3
x
Ax
+
=
−
và
1 7 3
9
3
x x
Bx
x
− −
= +
+
1. Tính A khi x = 25.
2. Rút g6n biu th$c B.
3. Tìm giá tr: nh; nh<t c=a
A
B
.
Hưng dn:
ðKXð:
0, 9
x x
≥ ≠
1. VRi x = 25 (TMðK) =>
25 5 30
15
5 3
25 3
A
+
= = =
−
−
2. Có:
1 7 3 ( 1)( 3) 7 3
9 9
3 ( 3)( 3)
4 3 7 3 3
9 9 3
x x x x x
Bx x
x x x
x x x x x x
x x x
− − − − −
= + = +
− −
+ + −
− + + − +
= = =
− − −
3. Có:
5 5
:
3 3
A x x x
B
x x x
+ +
= =
− −
ðK: x > 0.
=>
5 5 5
2. 2 5
A x x x
Bx x x
+
= = + ≥ =i
D<u "=" x?y ra <=>
5
5( )
x x TM
x
= ⇔ =
Vhy
2 5 5
MinA x
= ⇔ =
Câu 2. (2,5 ñim)
1. Gi?i phương trình:
a)
2
5 4 0
x x
− + =
b)
4 2
6 0
x x
+ − =
2. Gi?i hF phương trình:
2 7
2 1
x y
x y
− =
− = −
Hưng dn:
1. a)
2
1
5 4 0
4
x
x x x
=
− + = ⇔
=
b)
2
4 2 2 2
2
( 2) 0 2
6 0 ( 2)( 3) 0 ( 3) 0( )
x x
x x x x x Voly
− = ⇔ = ±
+ − = ⇔ − + = ⇔ + =
2.
2 7 4 2 14 3 15 5
2 1 2 1 2 1 3
x y x y x x
x y x y x y y
− = − = = =
⇔ ⇔ ⇔
− =− − =− − = − =
Câu 3. (1,0 ñim)
Cho phương trình:
2
1 0
x ax b
+ + + =
(a, b là các tham sI). Tìm a, b ñ phương trình có 2 nghiFm x1, x2 th;a
mãn: 1 2
3 3
1 2
3
9
x x
x x
− =
− =
Hưng dn:
Ta có:
2 2
4( 1) 4 4
a b a b
= − + = − −
ð phương trình có nghiFm thì:
2
0 4 4 0
a b
≥ ⇔ − − ≥
Theo VijEt ta có:
1 2
1 2
. 1
x x a
x x b
− = −
= +
Mà:
1 2 1 2 2
1 2 1 2
3 3 2 2
1 2 1 2 1 1 2 2
3 3
( ) 3
9 ( )( ) 9
x x x x x x x x
x x x x x x x x
− = − =
⇔ ⇔ + − =
− = − + + =
2 2
( ) 1 3 4
a b b a
⇔ − − − = ⇔ = −
Thay
2
4
b a
= −
vào biu th$c Delta ta có:
2 2 2 2
4 4 4( 4) 4 3 12
a b a a a
= − − = − − − = − +
ðK:
2
0 3 12 0 2 2
a a
≥ ⇔ − − ≥ ⇔ − ≤ ≤
=>
2 2
1 2
3 12 3 12
;
2 2 2 2
a a a a
a a
x x
− + − + − − − +
− + − −
= = = =
Do:
2 2
1 2 1 2
2
3 12 3 12
3 3
2 2
1
3 12 9 ( ) 3
1
a a a a
x x x x
a
a TM b
a
− + − + − − − +
− = => − = − =
=
=>− + = => => = −
=−
Vhy
1
3
a
b
= ±
= −
thì pt có nghiFm th;a mãn ñk bài.
Câu 4. (3,0 ñim)
Cho t$ giác ABCD nLi tiMp (O; R) và có hai ñưOng chéo AC, BD vuông góc vRi nhau tSi I (I khác O). KU
ñưOng kính CE.
1. Ch$ng minh t$ giác ABDE là hình thang cân.
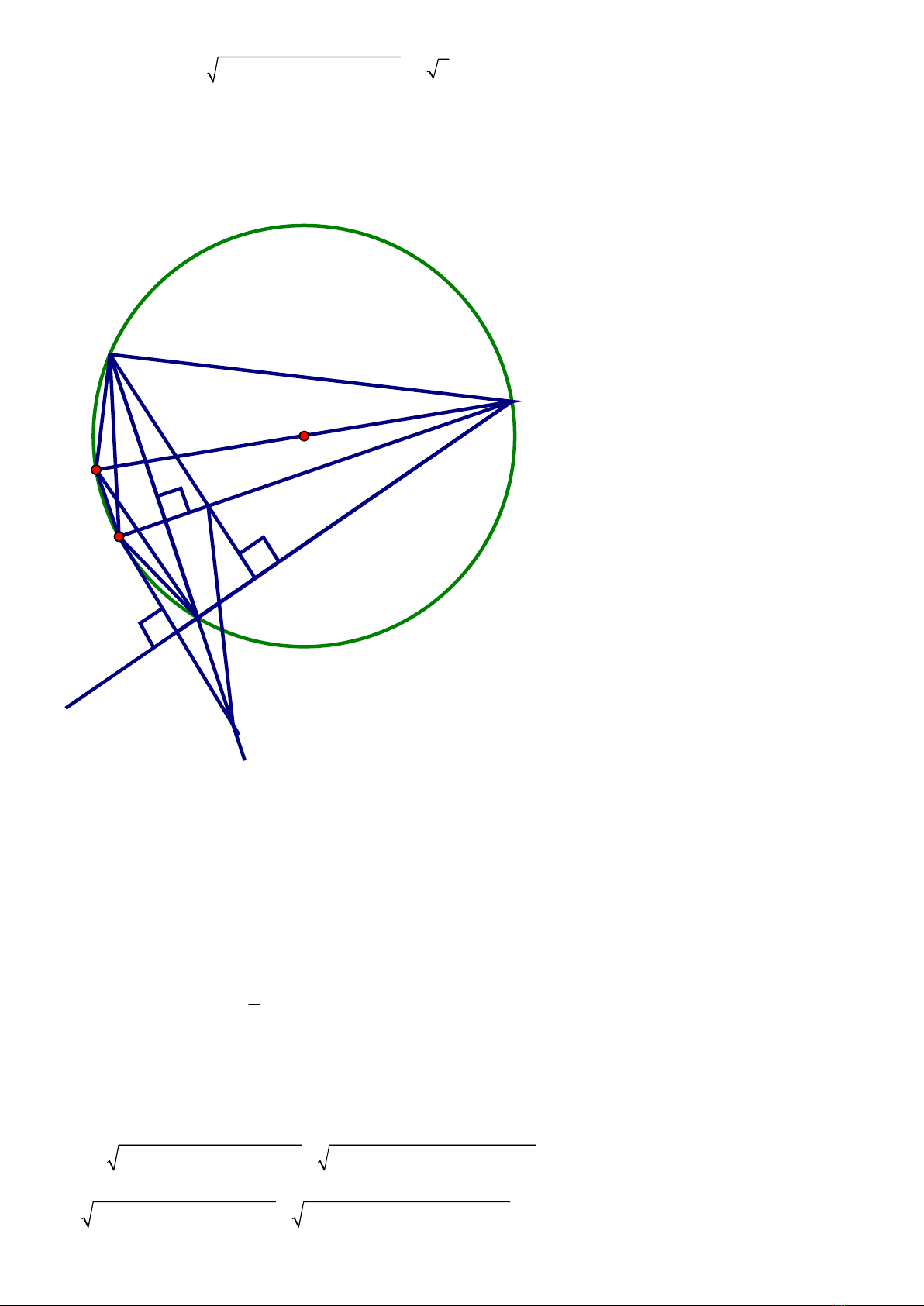
2. Ch$ng minh:
2 2 2 2
2 2 .
AB CD BC AD R
+ + + =
3. TX A, B kU các ñưOng thYng vuông góc vRi CD lZn lư[t c\t BD, AC tSi F và K. T$ giác ABKF là hình
gì?
HưHng dIn:
1. Có:
0
90
EAC EBC EDC= = =
(Góc nt ch\n nla ñưOng tròn)
EA AC
⇒ ⊥
( )
EA BD AC
⇒ ⊥
EADB
⇒
là hình thang (1)
Mà:
0
0
90
90
BEC BCE
IDC ICD
= =
= =
(cmt)
Do:
1
2
IDC BDC ADC BC
= = =
(Góc nt ch\n
BC
)
=>
ICD ACD BCE
= =
=>
EB AD EB AD
⇒ = ⇒ =
(2)
TX (1) và (2) => AEBD là hình thang cân. (ñpcm)
2. Có:
2 2 2 2 2 2 2 2
( ) ( )
AB CD BC AD ED CD BC EB
+ + + = + + +
(Vì: AB = ED, AD = EB (cmt))
=>฀AB
2
+฀CD
2
+฀BC
2
+฀AD
2
=฀(ED
2
+฀CD
2
) +฀(BC
2
+฀EB
2
)
O
K
F
C
B
E
D
I
M
N
A
(ñpcm)
3. Gi? sl :
AF ;
CD M BK CD N
⊥ = ⊥ =
=>
IF
MCA A
=
(Cùng pho vRi
CAM
)
AF
B
⇒
cân tSi A. => AB = AF (3)
IAF
IAB⇒ =
(ðưOng cao trong tam giác cân)
Mà: BK // AF (cùng
DC
⊥
)
IAF ( )
IKB SLT
⇒ =
IAB ( IAF)
IKB⇒ = =
A
BK
⇒
cân tSi B => BA = BK (4)
TX (3) và (4) => AB = BK = AF.
=> AF//=BK => ABKF là HBH
Mrt khác: => ABKF là hình thoi.
Câu 5. (1,0 ñim)
1. Tìm nghiFm nguyên c=a phương trình:
3 3 2
1.
y x x x
= + + +
2. Cho các sI nguyên a, b, c th;a mãn ab + bc + ca = 1. Ch$ng minh rbng: A =
(
)
(
)
(
)
2 2 2
1 1 1
a b c
+ + +
là
mLt sI chính phương.
Hưng dn:
1. VRi y = 0 =>
3 2 2
1 0 ( 1)( 1) 0
x x x x x
+ + + = ⇔ + + =
<=>
2
( 1) 0 ( : 1 0 )
x Do x x
+ = + > ∀
<=> x = j1.
VRi y
0
≠
=> y.y2 = (x + 1)(x2 + 1)
=> 2 2
1
1
y x
y x
= +
= +
(Vì:
2 2
, , 1 1)
x y y y x x
∈ ⇒ < + < +
ℤ
2 2 2 2
( 1) 1 2 1 1 0
x x x x x x
+ = + ⇔ + + = + ⇔ =
=> y = 1
Vhy pt có nghiFm là: (x;y) = (j1; 0) ; (0; 1)
2. Vì: ab+bc+ca = 1 => 1 + a2 = ab+bc+ca + a2 = (a+b)(a+c) (1)
Tương ts: 1 + b2 = ab+bc+ca + b2 = (a+b)(b+c) (2)
1 + c2 = ab+bc+ca + c2 = (c+b)(a+c) (3)
2 2 2 2
2 2.(2 ) 2 2
EC EC EC R R
= + = = =