
Tài liệu ôn tập Toán tài chính
2013
1
SV: Ngô Thị Linh Hòa – KT 4D - QUI
HỆ THỐNG HÓA KIẾN THỨC HỌC PHẦN TOÁN TÀI CHÍNH
Chƣơng I: LÃI ĐƠN – LÃI KÉP
A. Lãi đơn
1. Lợi tức:
Lợi tức là số tiền mà người sử dụng vốn (người vay) phải trả cho người sở hữu vốn (người cho
vay) để được sử dụng vốn trong thời gian nhất định.
Những rủi ro có thể gặp khi cho vay:
Người vay vốn không trả lãi.
Người vay vốn không hoàn trả vốn vay.
2. Lãi đơn
Lãi đơn là lợi tức chỉ tính trên số vốn vay ban đầu trong suốt thời hạn vay.
3. Lãi suất (tỷ suất lợi tức)
Lãi suất là tỷ số giữa lãi phải trả trong một đơn vị thời gian với số vốn vay.
Đơn vị thời gian: năm, tháng, ngày,…
Lãi suất thường được ghi dưới dạng %, ngoài ra còn có thể ghi dưới dạng số lẻ thập phân.
4. Giá trị đạt được
Giá trị đạt được là tổng số tiền thu được sau khi kết thúc đợt đầu tư.
Giá trị đạt được bao gồm 2 phần: vốn gốc và lãi thu được.
Trong đó:
: là giá trị đạt được tính đến thời điểm .
: là thời gian cho vay (ngày, tháng, quý, năm,…)
: là số vốn gốc.
: là lãi suất.
: là số tiền lãi.
Chú ý:
&in
phải đồng nhất đơn vị.
Nếu
i
tính theo năm còn
n
tính theo tháng thì:
Nếu
i
tính theo tháng còn
n
tính theo ngày thì:
Nếu
i
tính theo năm còn
n
tính theo ngày thì:
0..
360
V i n
I
hoặc
0..
365
V i n
I
5. Lãi suất ngang giá.

Tài liệu ôn tập Toán tài chính
2013
2
SV: Ngô Thị Linh Hòa – KT 4D - QUI
Hai lãi suất
&k
ii
tương ứng với 2 chu kỳ khác nhau được gọi là tương đương nhau khi cùng 1 số
vốn, đầu tư trong cùng 1 thời gian thì cho cũng mức lãi suất như nhau.
k
i
ik
6. Tỷ suất lợi tức bình quân.
1
1
.
n
jj
j
n
j
j
ni
i
n
Trong đó:
i
: Lãi suất bình quân.
j
n
: Thời gian kỳ thứ
j
.
j
i
: Lãi suất của kỳ thứ
j
.
7. Lãi suất thực
Lãi suất thực là mức chi phí (lãi) thực tế mà người đi vay phải trả để sử dụng 1 khoản vốn vay nào
đó trong 1 thời hạn nhất định.
0
360
t
t
t
I
iV C n
Trong đó:
t
i
: Lãi suất thực.
t
I
: Chi phí thực tế trong thời gian vay.
t
C
: Chi phí thực tế trả ngay khi vay.
B. Lãi kép
1. Khái niệm.
Lãi kép là lãi được nhập vào vốn để tính lãi cho kỳ sau.
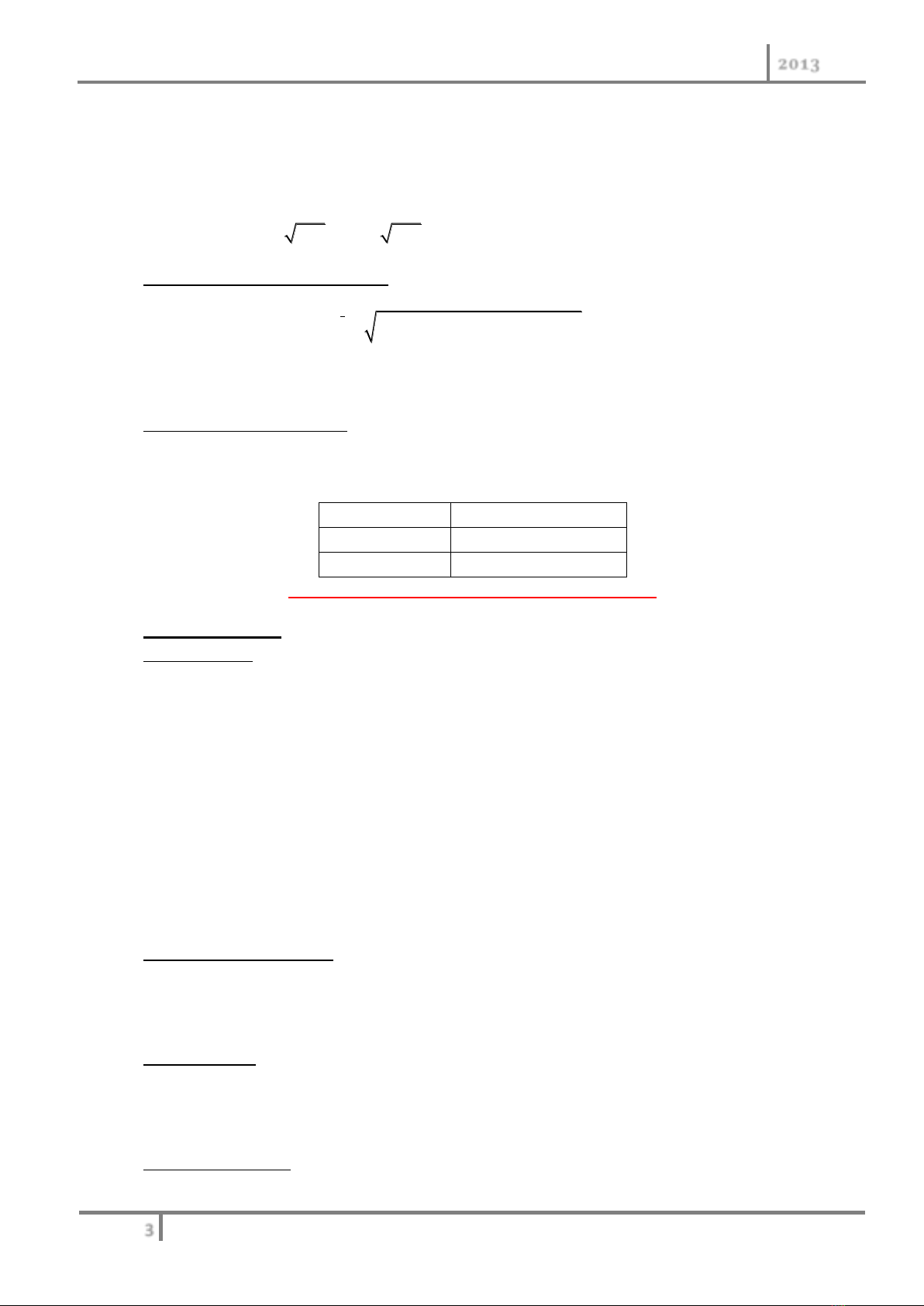
0.1 n
n
V V i
Lãi kép phản ánh giá trị theo thời gian của tiền tệ cho cả phần vốn gốc lẫn tiền lãi do nó sinh ra.
2. Vốn đầu tư ban đầu.
0.1
1
n
n
n
n
V
V V i
i
3. Thời gian đầu tư.
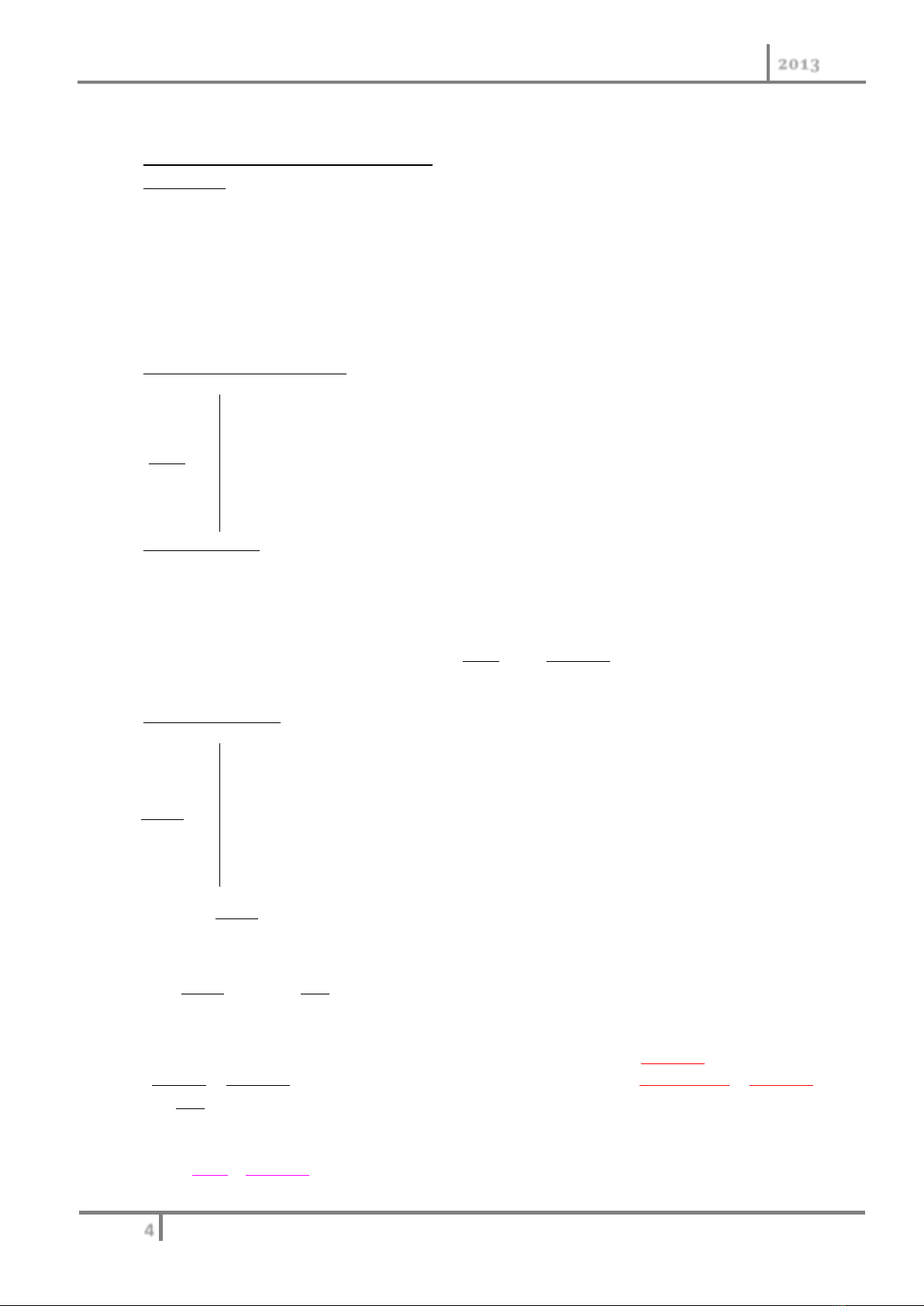
000
1
0
lg ln
1 log lg 1 ln 1
n
nn
V
nV
n
i
VV
VV
V
in
V i i
4. Lãi suất đầu tư.
00
11
nnn
n
VV
ii
VV
5. Lãi suất ngang giá.
Tài liệu ôn tập Toán tài chính
2013
3
SV: Ngô Thị Linh Hòa – KT 4D - QUI
Hai lãi suất
&k
ii
tương ứng với 2 chu kỳ khác nhau được gọi là tương đương nhau khi cùng 1 số
vốn, đầu tư trong cùng 1 thời gian thì cho cùng mức lãi như nhau.
Hay tổng quát:
1 1 1 1
kk
i i i i
6. Lãi suất bình quân trong lãi kép.
1 2 2
12
1 . 1 ... 1 1
n n k
n
k
i i i i
Với
1 2 3 ... k
n n n n n
7. So sánh lãi đơn với lãi kép.
Với cùng số vốn đầu tư
0
V
:
1n
1n
1n
Chƣơng II: CHIẾT KHẤU THƢƠNG PHIẾU
A. Một số khái niệm
1. Thương phiếu.
Thương phiếu là giấy cam kết trả nợ tiền mua hàng trả chậm, thực chất là giấy nhận nợ, người nhận
nợ cam kết trả nợ vô điều kiện trong 1 thời gian nhất định.
Thương phiếu được thể hiện dưới 2 hình thức:
Hối phiếu: do người bán lập.
Lệnh phiếu (kỳ phiếu): khách hàng trực tiếp lập và ký vào lệnh phiếu.
Trên một thương phiếu cần xác định rõ:
Mệnh giá của thương phiếu (giá trị danh nghĩa) là số tiền phải trả.
Ngày đáo hạn là ngày trả tiền.
2. Chiết khấu thương phiếu.
Là 1 nghiệp vụ tín dụng thực hiện bằng việc bán lại thương phiếu chưa đáo hạn cho Ngân hàng.
(Hình thức cho vay đặc biệt – người vay đem thương phiếu chưa đáo hạn đến bán cho Ngân hàng.)
3. Phí chiết khấu.
Là khoản lãi mà DN phải trả khi vay vốn của Ngân hàng dưới hình thức chiết khấu thương phiếu,
thời hạn tính từ ngày chiết khấu đến ngày đáo hạn.
4. Lãi suất chiết khấu.
Tài liệu ôn tập Toán tài chính
2013
4
SV: Ngô Thị Linh Hòa – KT 4D - QUI
Là lãi suất do Ngân hàng quy định khi áp dụng cho nghiệp vụ chiết khấu.
B. Chiết khấu thƣơng mại theo lãi đơn.
1. Khái niệm.
Là 1 NV tín dụng, qua đó Ngân hàng tính phí chiết khấu ngay khi NV chiết khấu phát sinh (người
vay phải trả trước lãi vay và các khoản chi phí ngay khi nhận tiền vay).
CKTM: Tính lãi trên mệnh giá của thương phiếu (trên cả vốn vay và lãi vay).
Lãi trả trước.
2. Phí chiết khấu thương mại.
..
360
C
C i n
e
Trong đó:
C
e
: Phí chiết khấu thương mại.
C
: Mệnh giá thương phiếu.
i
: Lãi suất chiết khấu.
n
: Thời gian tính từ ngày chiết khấu đến ngày đáo hạn (tính 1 đầu mút: tính
ngày đầu, ko tính ngày cuối).
3. Giá trị hiện tại.
Giá trị hiện tại (hay thời giá của thương phiếu): là số tiền thực tế Ngân hàng phải trả cho người có
thương phiếu ngay khi chiết khấu.
0
. . 360 .
360 360
C
C i n i n
V C e C C
4. Chiết khấu hợp lý.
0..
360
V i n
e
Trong đó:
e
: Phí chiết khấu hợp lý.
0
V
: Giá trị gốc (hiện giá) của thương phiếu.
i
: Lãi suất chiết khấu.
n
: Thời gian tính từ ngày chiết khấu đến ngày đáo hạn (tính 1 đầu mút: tính
ngày đầu, ko tính ngày cuối).
0
0
..
360
V i n
V C e C
0
00
.. .
.1
360 360
V i n in
C V V
0
360.
.360 .
1360
CC
Vin in
Thay vào CT tính chiết khấu hợp lý ta có:
360. .. ..
360 .
360 360 .
Cin C i n
in
ein
Vậy:
. . . .
360 360 .
C
C i n C i n
ee in
Tài liệu ôn tập Toán tài chính
2013
5
SV: Ngô Thị Linh Hòa – KT 4D - QUI
Trên thực tế:
C
ee
.
5. Ngang giá của 2 thương phiếu.
2 thương phiếu được xem là tương đương nếu 1 ngày nào đó chúng có giá trị bằng nhau (theo
cùng 1 lãi suất chiết khấu). Ngày đó được coi là ngày tương đương và phải xảy ra trước ngày
đáo hạn của thương phiếu.
1 thương phiếu được coi là tương đương với nhiều thương phiếu khác nếu giá trị hiện tại của
nó bằng tổng các thời giá của các thương phiếu khác.
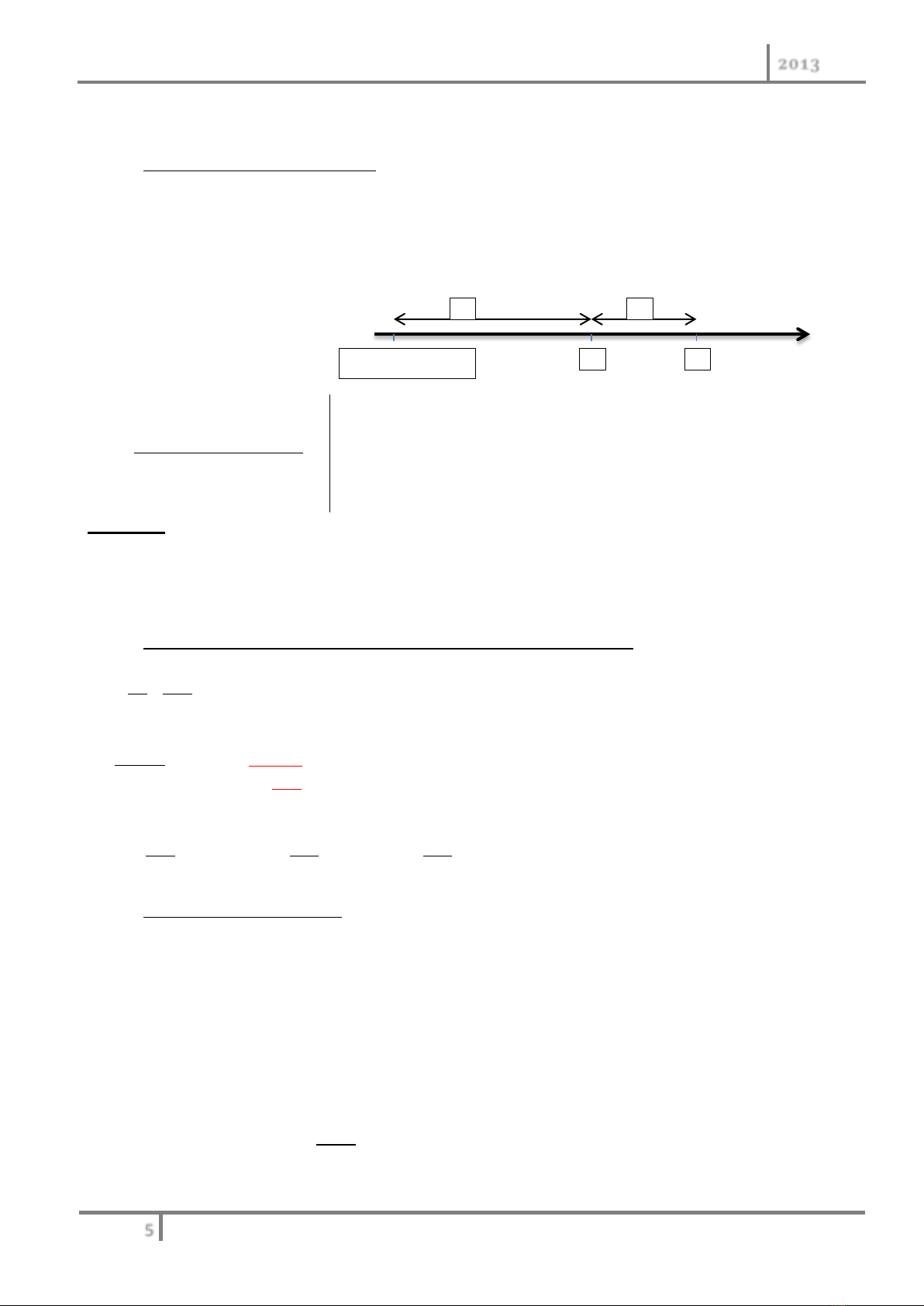
Xác định ngày ngang giá:
21
21
. 360 . 360.
.
C i y C
xi C C
Trong đó:
x
: thời gian từ ngày ngang giá đến ngày đáo hạn đầu tiên.
y
: thời gian từ ngày đáo hạn đầu tiên đến ngày đáo hạn của
thương phiếu thứ 2.
1
C
,
2
C
: mệnh giá của thương phiếu 1, 2.
Nhận xét:
2 thương phiếu có cùng mệnh giá nhưng có thời gian đáo hạn khác nhau thì chúng ko ngang
giá.
2 thương phiếu luôn luôn ngang giá nếu chúng có cùng mệnh giá và ngày đáo hạn.
6. Lãi suất chiết khấu hiệu dụng (LS chi phí chiết khấu thương mại).
0
360
C
hd
e
iVn
360.
.
C
e
iCn
Vậy
.
1360
hd
i
iin
Do
. . .
0 1 1 0 0 1 1
360 360 360
i n i n i n
hd
ii
7. Chi phí chiết khấu (AGIO)
Là toàn bộ những khoản tiền Ngân hàng trích lại khi chiết khấu thương phiếu.
AGIO chưa thuế:
Chi phí chiết khấu
=
Phí chiết khấu
+
Hoa hồng chiết khấu
+
Thuế
o Hoa hồng chiết khấu:
o Hoa hồng cố định:
.kC
(hoặc
0
.kV
), khoản cho trước.
o Hoa hồng ký hậu (
i
):
..
360
C i n
(tính như
C
e
).
x
y
Ngày tương đương
1
2
















