Khoa KTMT Vũ Đ c Lungứ1
Ch ng 4 – M ch Logic sươ ạ ố
4.1. C ng và đ i s Booleanổ ạ ố
4.1.1. C ng (Gate)ổ
4.1.2. Đ i s Booleanạ ố
4.2. B n đ Karnaughả ồ
4.3. Nh ng m ch Logic s c b nữ ạ ố ơ ả
4.3.1. M ch tích h p (IC-Intergrate Circuit)ạ ợ
4.3.2. M ch k t h p (Combinational Circuit)ạ ế ợ
4.3.3. B d n kênh-b phân kênhộ ồ ộ
4.3.4. M ch c ng (Adder)ạ ộ
4.3.5. M ch gi i mã và mã hóaạ ả
Khoa KTMT Vũ Đ c Lungứ2
4.1. C ng và đ i s Booleanổ ạ ố
M ch s là m ch trong đó ch hi n di n hai giá tr logic. ạ ố ạ ỉ ệ ệ ị
Th ng tín hi u gi a 0 và 1 volt đ i di n cho s nh phân 0 ườ ệ ữ ạ ệ ố ị
và tín hi u gi a 2 và 5 volt – nh phân 1.ệ ữ ị
C ng – c s ph n c ng, t đó ch t o ra ổ ơ ở ầ ứ ừ ế ạ
m i máy tính sọ ố
G i là c ng lu n lý vì nó cho k t qu lý lu n c a đ i s logic ọ ổ ậ ế ả ậ ủ ạ ố
nh n u A đúng và B đúng thì C đúng (c ng A AND B = C)ư ế ổ
Khoa KTMT Vũ Đ c Lungứ3
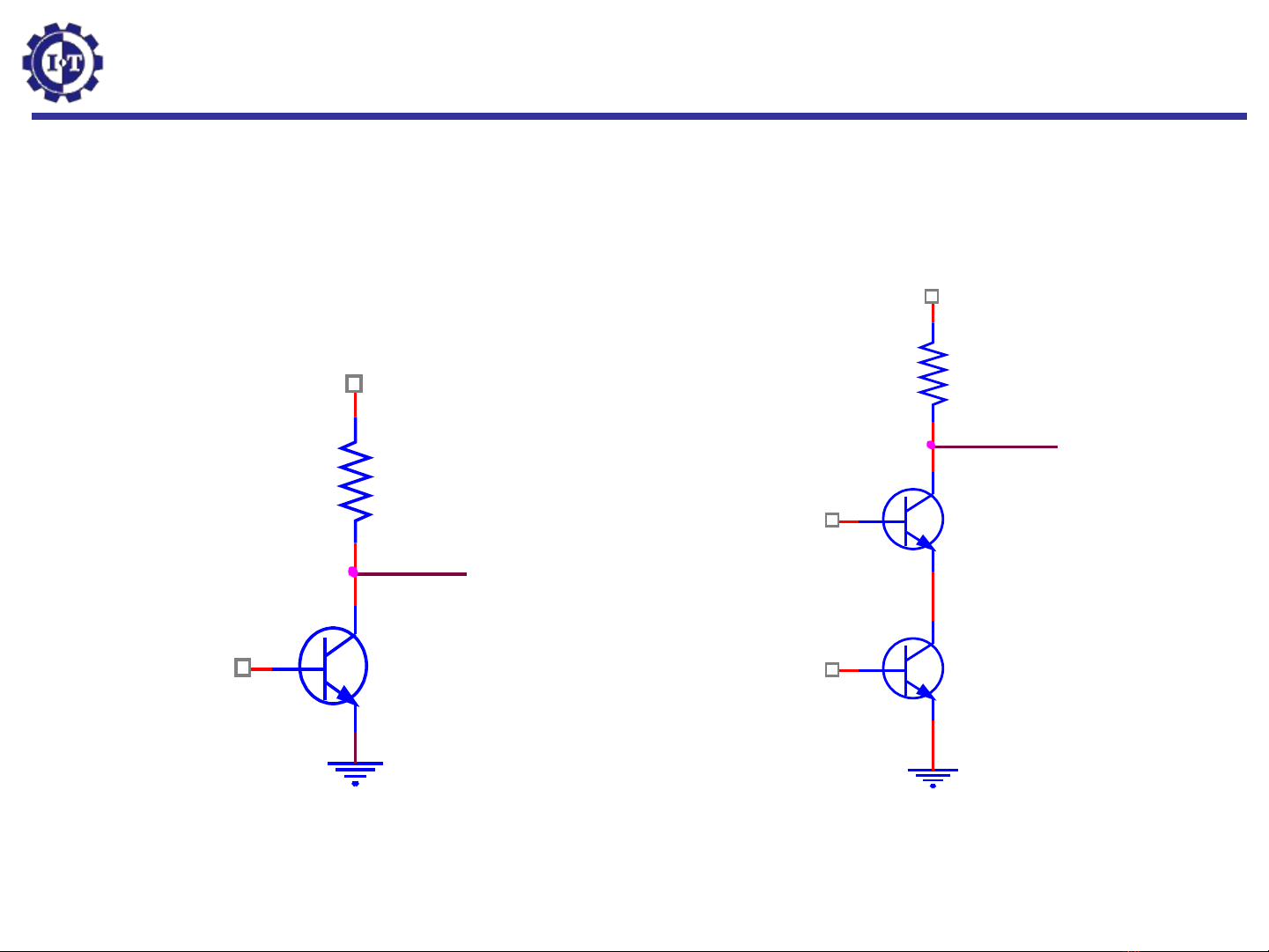
B chuy n đ i transistor – c ng ộ ể ổ ổ
(gate): C c góp (collector), c c n n ự ự ề
(base), c c phát (emitter)ự
a) C ng INV (NOT)ổ
Cổng NAND
b)
1 2
G N D
1
23
V i n
V o u t
+ V c c
Base
C o l l e c t o r
E m i t e r
1 2
1
23
1
23
U 5
G N D
V 1
V 2
V o u t
4.1.1. C ng (Gate)ổ
Khoa KTMT Vũ Đ c Lungứ4
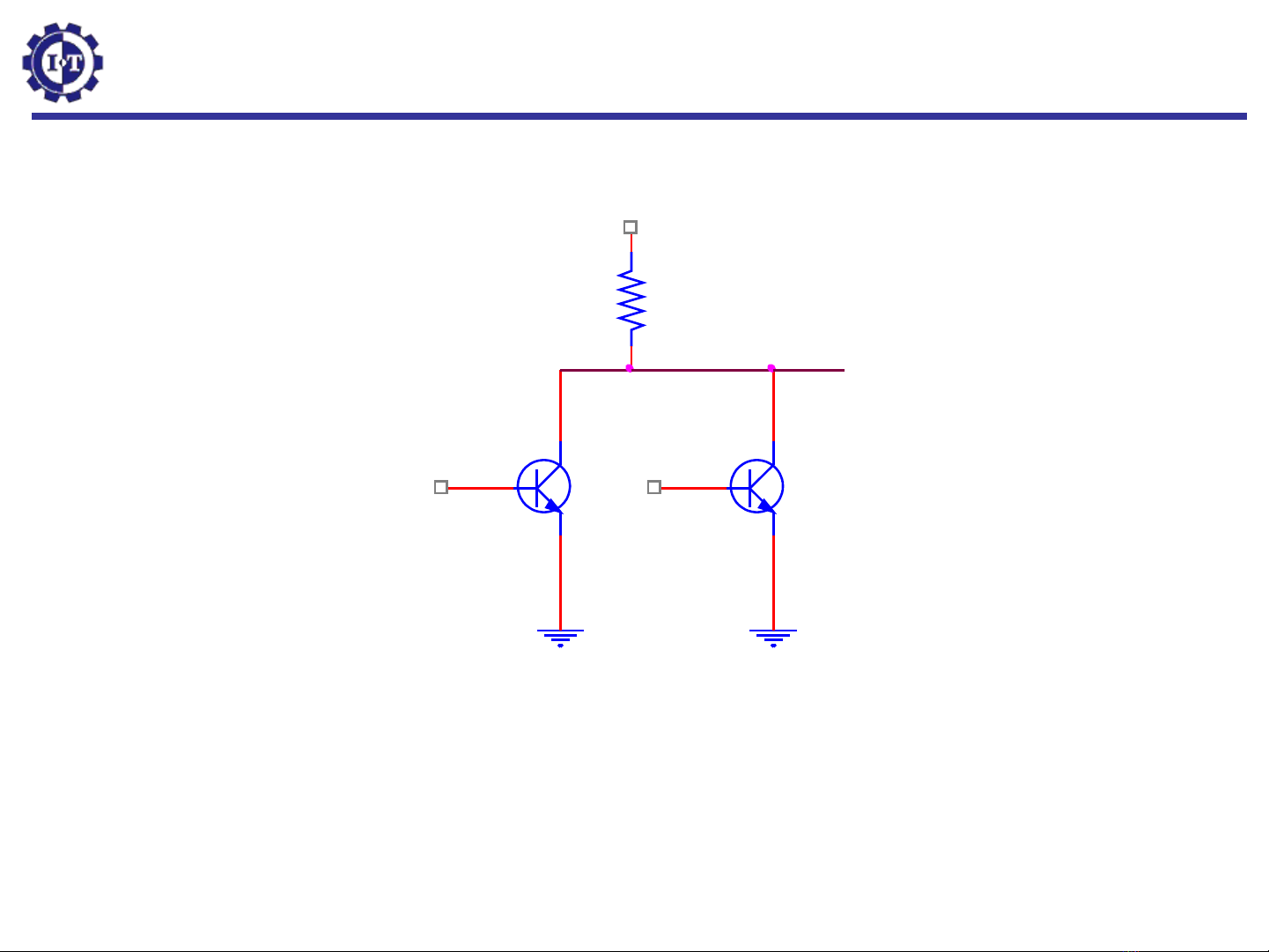
4.1.1. C ng (Gate)ổ
C ng NORổ
1 2
3
1 3
2
1 3
2
V o u t
+ V c c
V 1 V 2
Khoa KTMT Vũ Đ c Lungứ5
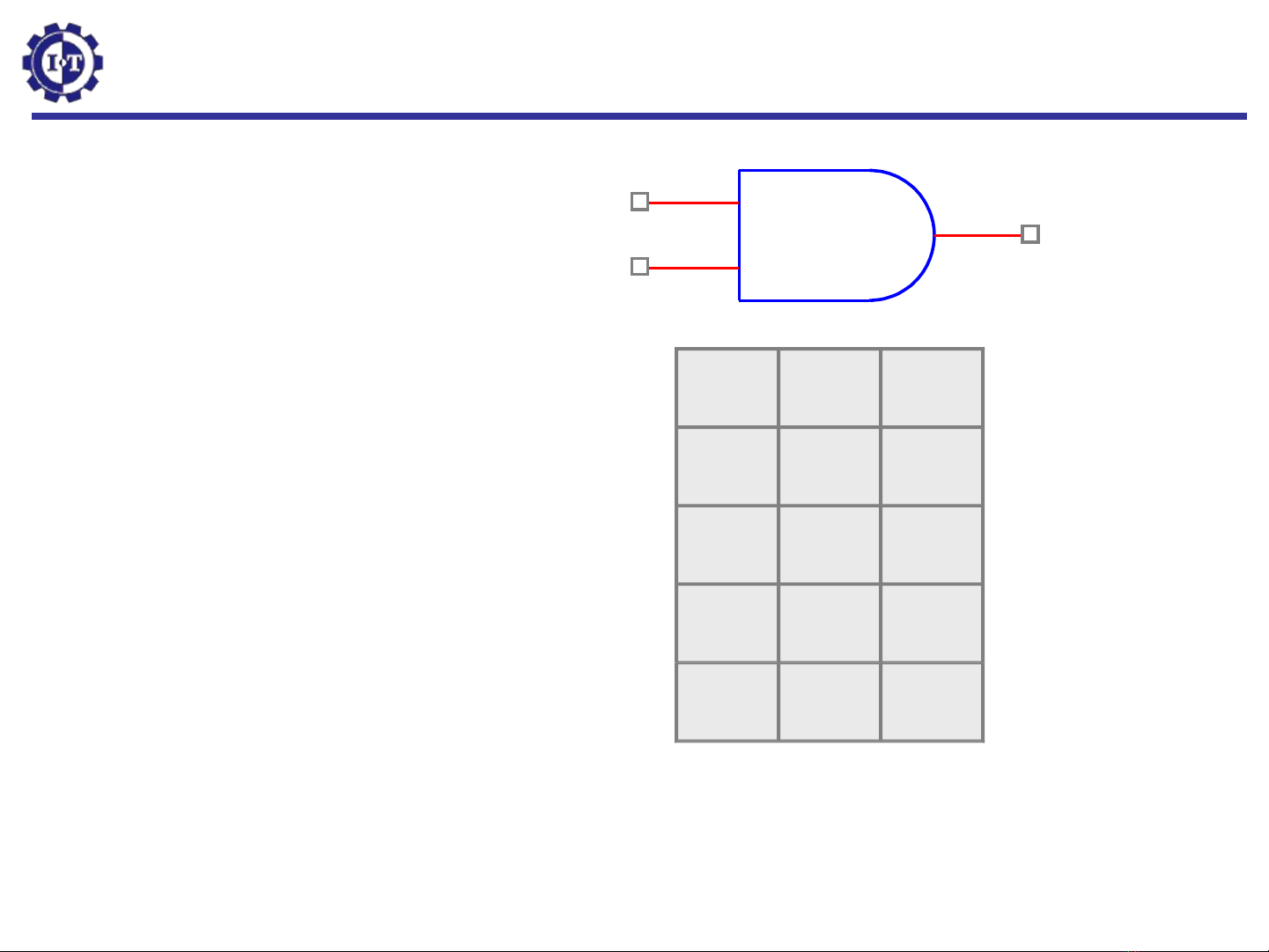
Các c ng c b n c a logic sổ ơ ả ủ ố
AND
OR
Inverter
NAND
NOR
XOR (exclusive-OR)
NXOR
A
Bx
A B x
000
010
100
111
AND
AND