Lập Trình Logic Trong ProLog - PGS.TS. PHAN HUY KHÁNH phần 3

Ng ngha ca chưng trình Prolog 31

 IAa%aD$!-a!ươ 

V! mt hình thc, ngha khai báo, hay ng ngha ch ý (intentional semantic)

xác nh các mi quan h ã ưc #nh ngha trong chương trình. Ngha khai báo

xác nh nhng gì là kt qu (ích) mà chương trình phi tính toán, phi to ra.

Ngha khai báo ca chương trình xác nh nu mt ích là úng, và trong

trưng hp này, xác nh giá tr ca các bin. Ta ưa vào khái nim th! nghim

(instance) ca mt mnh ! C là mnh ! C mà mAi mt bin ca nó ã ưc

thay th bi mt hng. Mt bin th! (variant) ca mt mnh ! C là mnh ! C

sao cho mAi mt bin ca nó ã ưc thay th bi mt bin khác.

Ví d II.1 : Cho mnh ! :

hasachild(X) :-

parent(X, Y).

Hai bin th ca mnh ! này là :

hasachild(A) :-

parent(A, B).

hasachild(X1) :-

parent(X1, X2).

Các th nghim ca mnh ! này là :

hasachild(tom) :-

parent(tom, Z).

hasachild(jafa) :-

parent(jafa, small(iago)).

Cho trưc mt chương trình và mt ích G, ngha khai báo nói r*ng :

Mt ích G là úng (tho mãn, hay suy ra ưc t chương trình mt cách

logic) nu và chD nu

(1) t>n ti mt mnh ! C ca chương trình sao cho

(2) t>n ti mt th nghim I ca mnh ! C sao cho:

(a) phn u ca I là ging ht G, và

(b) mi ích ca phn thân ca I là úng.

nh ngha trên ây áp dng ưc cho các câu h=i Prolog. Câu h=i là mt

danh sách các ích ngn cách nhau bi các du phGy. Mt danh sách các ích là

úng nu tt c các ích ca danh sách là úng cho cùng mt ràng buc ca các

bin. Các giá tr ca các bin là nhng giá tr ràng buc t1ng quát nht.

32 Lp trình lôgic trong Prolog

 3$LNL

Mt gói hay bó mnh  (packages of clauses) là tp hp các mnh ! có

cùng tên hng t chính (cùng tên, cùng s lưng tham i). Ví d sau ây là mt

gói mnh ! :

a(X) :- b(X, _).

a(X) :- c(X), e(X).

a(X) :- f(X, Y).

Gói mnh ! trên có ba mnh ! có cùng hng là a(X). MAi mnh ! ca gói

là mt phương án gii quyt bài toán ã cho.

Prolog quy ưc :

• mAi du ph.y (comma) t gia các mnh !, hay các ích, óng vai trò

phép hi (conjunction). V! mt lôgich, chúng phi úng tt c.

• mAi du chm ph.y (semicolon) t gia các mnh !, hay các ích, óng

vai trò phép tuy!n (disjunction). Lúc này chD cn mt trong các ích ca

danh sách là úng.

Ví d II.2 :

P :- Q; R.

ưc c là : P úng nu Q úng hoc R úng. Ngưi ta cBng có th vit tách ra

thành hai mnh ! :

P :- Q.

P :- R.

Trong Prolog, du phGy (phép hi) có mc  ưu tiên cao hơn du chm phGy

(phép tuyn). Ví d :

P :- Q, R; S, T, U.

ưc hiu là :

P :- (Q, R); (S, T, U).

và có th ưc vit thành hai mnh ! :

P :- (Q, R).

P :- (S, T, U).

Hai mnh ! trên ưc c là : P úng nu hoc c Q và R !u úng, hoc c

S, T và U !u úng.

V! nguyên t6c, th t thc hin các mnh ! trong mt gói là không quan

trng, tuy nhiên trong thc t, cn chú ý tôn trng th t ca các mnh !. Prolog

s@ ln lưt thc hin theo th t xut hin các mnh ! trong gói và trong chương

trình theo mô hình tun t b*ng cách th quay lui mà ta s@ xét sau ây.

Ng ngha ca chưng trình Prolog 33

( IAa!!-a!$!L

Ngha lôgich th hin mi liên h gia c t lôgich (logical specification)

ca bài toán cn gii vi bn thân chương trình.



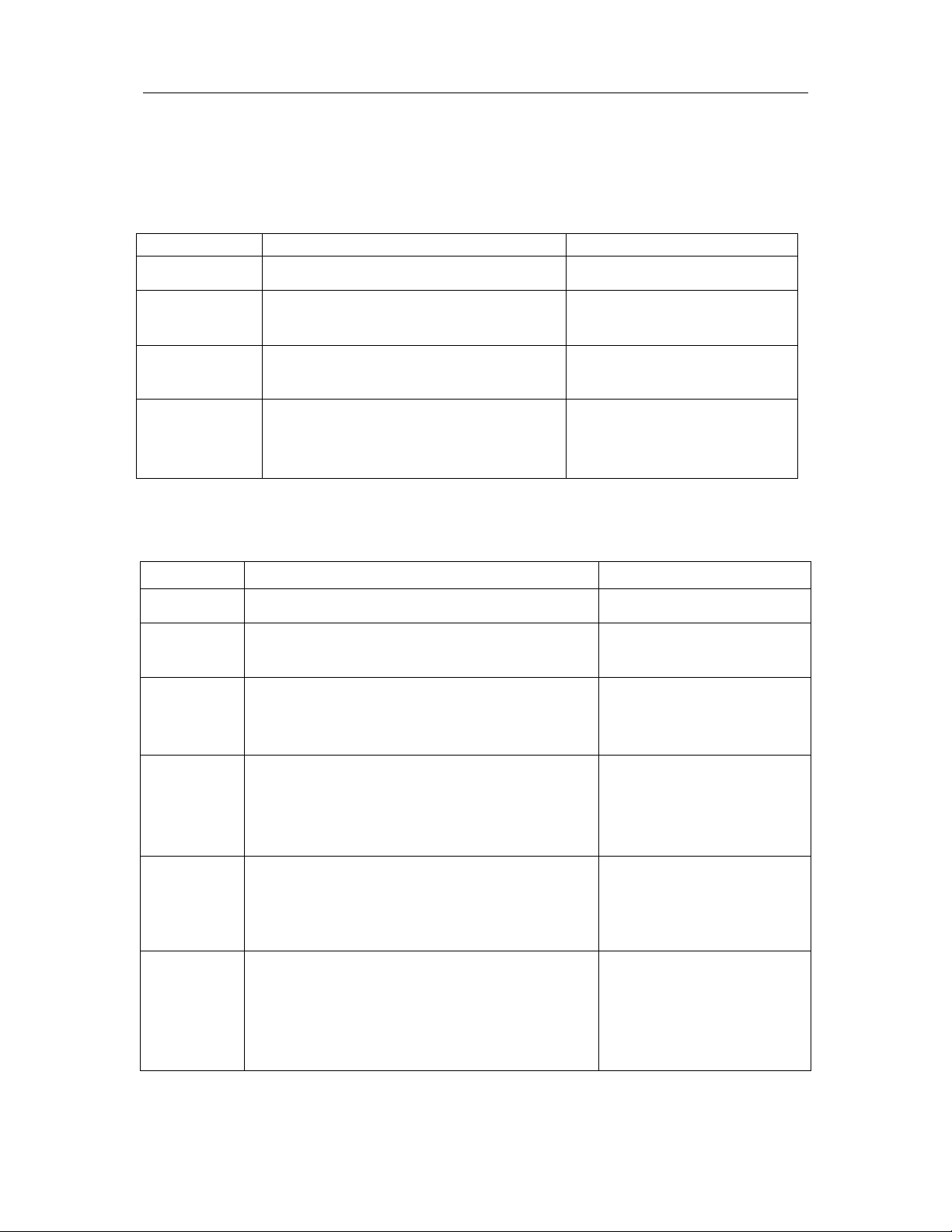
"$!L%!MaD;

Mnh  Ngha lôgich Ký hiu Toán hc

P(a). P(X) úng nu X = a P(X) ⇔ X = a

P(a).

P(b).

P(X) úng nu X = a hoc X = b P(X) ⇔ (X = a) ∨ (X

= b)

P(a) :-

Q(c).

P(X) úng nu X = a và Q(c)

úng P(X) ⇔ X = a ∧ Q(c)

P(a) :-

Q(c).

P(b).

P(X) úng nu hoc (X = a và

Q(c) úng) hoc X = b

P(X) ⇔ (X = a ∧

Q(c))

∨ (X = b)

Quy ưc : nu = nu và chD nu.



"$!L!N!MaD;

Mnh  Ngha lôgich Ký hiu Toán hc

P(X). Vi mi giá tr ca X, P(X) úng ∀X P(X)

P(X) :-

Q(X).

Vi mi giá tr ca X, P(X) úng nu

Q(X)

úng P(X) ⇔ Q(X)

P(X) :-

Q(X, Y).

Vi mi giá tr ca X, P(X) úng nu t

>n ti

Y là mt bin cc b sao cho Q(X, Y)

úng

P(X) ⇔ ∃Y Q(X, Y)

P(X) :-

Q(X,

_).

Vi mi giá tr ca X, P(X) úng nu t

>n ti

mt giá tr nào ó ca Y sao cho Q(X, Y)

úng (không quan tâm n giá tr ca Y như

th nào)

P(X) ⇔ ∃Y Q(X, Y)

P(X) :-

Q(X,

Y),

R(Y).

Vi mi giá tr ca X, P(X) úng nu t

>n ti

Y sao cho Q(X, Y) và R(Y) úng

P(X) ⇔ ∃Y Q(X, Y) ∧

R(Y)

P(X) :-

Q(X,

Y),

R(Y).

p(a).

Vi mi giá tr ca X, P(X) úng nu hoc

t>n ti Y sao cho Q(X, Y) và R(Y) úng,

hoc X = a

P(X) ⇔ (∃Y Q(X, Y)

∧ R(Y))

∨ (X = a)

34 Lp trình lôgic trong Prolog

(

IAa!!-a!$!)!

*ích Ngha lôgich

p(a). Có phi p(a) úng (tho mãn) ?

p(a), Q(b). Có phi c p(a) và Q(b) !u úng ?

P(X). Cho bit giá tr ca X  P(X) là úng ?

P(X), Q(X, Y). Cho bit các giá tr ca X và ca Y  P(X) và Q(X,

Y) !u là úng ?

 IAa-C!!-a

Ngha th tc, hay ng ngha thao tác (operational semantic), li xác nh

làm cách nào  nhn ưc kt qu, ngha là làm cách nào  các quan h ưc

x lý thc s bi h thng Prolog.

Ngha th tc tương ng vi cách Prolog tr li các câu h=i như th nào

(how) hay lp lun trên các tri thc. Tr li mt câu h=i có ngha là tìm cách xóa

mt danh sách. i!u này chD có th thc hin ưc nu các bin xut hin trong

các ích này ưc ràng buc sao cho chúng ưc suy ra mt cách lôgich t

chương trình (hay t các tri thc ã ghi nhn).

Prolog có nhim v thc hin ln lưt tng ích trong mt danh sách các ích

t mt chương trình ã cho. «Thc hin mt ích» có ngha là tìm cách tho mãn

hay xoá ích ó kh=i danh sách các ích ó.

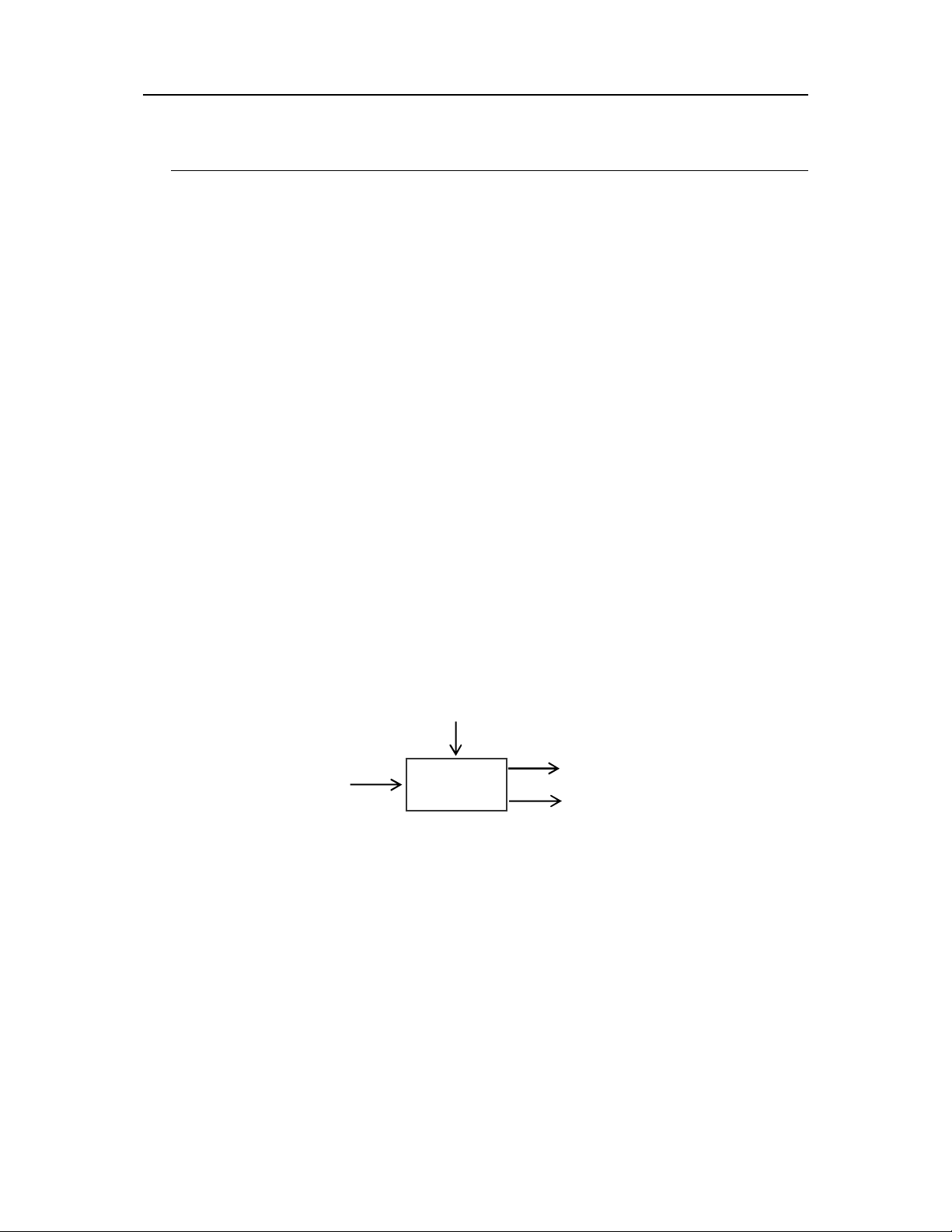
Hình II.1. Mô hình vào/ra ca mt th tc thc hin mt danh sách các ích.

Gi th tc này là execute (thc hin), cái vào và cái ra ca nó như sau :

Cái vào : mt chương trình và mt danh sách các ích

Cái ra : mt du hiu thành công/tht bi và mt ràng buc các bin

Ngha ca hai cái ra như sau :

(1) Du hiu thành công/tht bi là Yes nu các ích ưc tho mãn (thành công),

là No nu ngưc li (tht bi).

(2) S ràng buc các bin chD xy ra nu chương trình ưc thc hin.

chương trình (s kin+lut)

danh sách các ích

execute

du hiu thành

công/tht bi

ràng bu

c các bin

Ng ngha ca chưng trình Prolog 35

Ví d II.3 :

Minh ho cách Prolog tr li câu h=i cho ví d chương trình gia h trưc ây

như sau :

ích cn tìm là :

?- ancestor(tom, sue)

Ta bit r*ng parent(bill, sue) là mt s kin.  s dng s kin này

và lut 1 (v! t1 tiên trc tip), ta có th kt lun r*ng ancestor(bill, sue).

ây là mt s kin kéo theo : s kin này không có mt trong chương trình,

nhưng có th ưc suy ra t các lut và s kin khác. Ta có th vit gn s suy

din này như sau :

parent(bill, sue)  ancestor(bill, sue)

Ngha là parent(bill, sue)kéo theo ancestor(bill, sue) bi lut

1. Ta li bit r*ng parent(tom, bill) cBng là mt s kin. Mt khác, t s

kin ưc suy din ancestor(bill, sue), lut 2 (v! t1 tiên gián tip) cho

phép kt lun r*ng ancestor(tom, sue). Quá trình suy din hai giai on này

ưc vit :

parent(bill, sue)  ancestor(bill, sue)

parent(tom, bill) và ancestor(bill, sue) 

ancestor(tom, sue)

Ta va chD ra các giai on  xoá mt ích, gi là mt chng minh. Tuy

nhiên, ta chưa chD ra làm cách nào Prolog nhn ưc mt chng minh như vy.

Prolog nhn ưc phép chng minh này theo th t ngưc li nhng gì ã

trình bày. Thay vì xut phát t các s kin cha trong chương trình, Prolog b6t

u bi các ích và, b*ng cách s dng các lut, nó thay th các ích này bi các

ích mi, cho n khi nhn ưc các s kin sơ cp.

 xoá ích :

?- ancestor(tom, sue).

Prolog tìm kim mt mnh ! trong chương trình mà ích này ưc suy din

ngay lp tc. Rõ ràng chD có hai mnh ! tho mãn yêu cu này là lut 1 và lut

2, liên quan n quan h ancestor. Ta nói r*ng phn u ca các lut này

tưng ng vi ích.

Hai mnh ! này biu din hai kh nng mà Prolog phi khai thác x lý.

Prolog b6t u chn x lý mnh ! th nht xut hin trong chương trình :

ancestor(X, Z) :- parent(X, Z).

Do ích là ancestor(tom, sue), các bin phi ưc ràng buc như sau :

Lập Trình Logic Trong ProLog - PGS.TS. PHAN HUY KHÁNH phần 3

Nguyên lý của prlog dựa trên phép suy diễn logic, liên quan đến những khái niệm toán học như phép hợp nhất herbran, hợp giả Robinson, logic vị từ bậc một

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi