BẢO MẬT THÔNG TIN
BÀI 3:
MÃ HÓA ĐỐI XỨNG HIỆN ĐẠI
Nguyễn Hữu Thể
1
Nội dung
1. TinyA5/1 2. A5/1 3. TinyRC4 4. RC4
2
bản tin ngôn ngữ,
một đơn vị mã hóa là chữ cái,
phương thức thay thế hay phương thức hoán vị.
Mã hóa cổ điển
HTML, hình ảnh, video, âm thanh…
=> Biểu diễn trên máy vi tính dưới dạng một dãy các số nhị
phân.
Trong máy tính: chữ cái được biểu diễn bằng mã ASCII.
Thông tin ngày ngày nay
3
Ví dụ:
Bản tin: attack
Mã ASCII: 97 116 116 97 99 107
01100011 01101011
Biểu diễn nhị phân: 01100001 01110100 01110100 01100001
4
Mã hóa đối xứng hiện đại
Ví dụ mã hóa đối xứng hiện đại
Nếu có bản rõ là “head” => nhị phân là: 111100000011
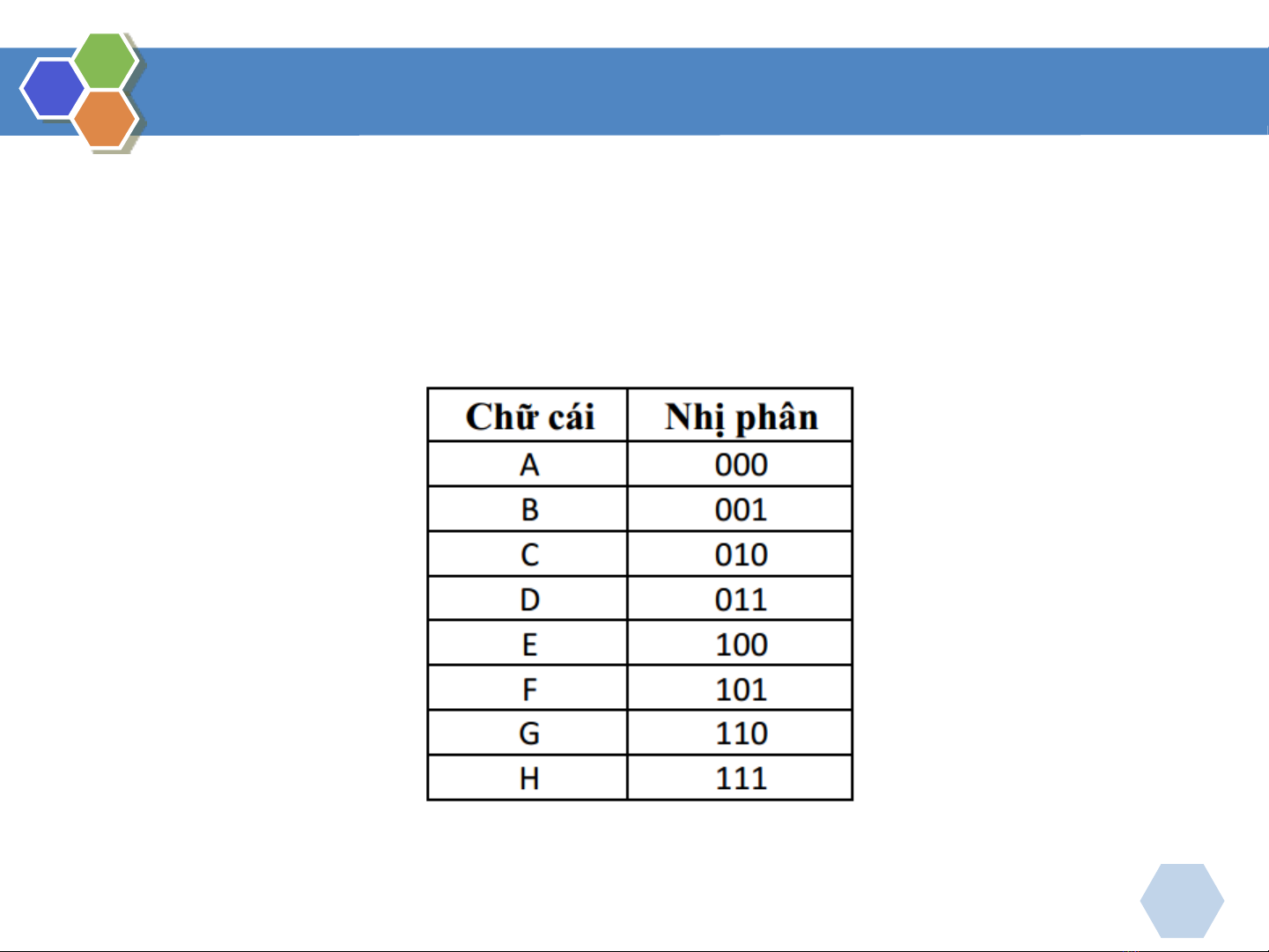
Bản rõ là các chữ cái của một ngôn ngữ gồm có 8 chữ cái A, B, C, D, E, F, G, H trong đó mỗi chữ cái được biểu diễn bằng 3 bít.
5
Mã hóa đối xứng hiện đại
bằng phép XOR :
bản rõ:
1111 0000 0011 (head)
khóa:
0101 0101 0101
bản mã:
1010 0101 0110 (FBCG)
Giả sử dùng một khóa K gồm 4 bít 0101 để mã hóa bản rõ trên
Đơn vị mã hóa không phải là một khối 4 bít.
bản rõ ban đầu.
Để giải mã, lấy bản mã XOR một lần nữa với khóa thì có lại
6
Mã hóa đối xứng hiện đại
Khóa được lặp lại:
• => điểm yếu giống như mã hóa Vigenere.
• Khắc phục: dùng một bộ sinh số ngẫu nhiên để tạo khóa dài,
giả lập mã hóa One-Time pad.
Một khối được mã hóa bằng phép XOR với khóa:
• => Không an toàn vì chỉ cần biết một cặp khối bản rõ - bản mã
(vd: 1111 và 1010) => dễ dàng tính được khóa.
• Khắc phục: tìm các phép mã hóa phức tạp hơn phép XOR
Mã hóa bằng phép XOR:
7
Mã dòng (Stream Cipher)
Mã dòng có các đặc tính sau:
8
Mã dòng (Stream Cipher)
Bản mã C được XOR với dãy số ngẫu nhiên S để cho ra
lại bản rõ ban đầu:
Giải mã => thực hiện ngược lại
Về phương diện khóa, ví dụ này giống mã Vigenere.
Ví dụ này không phải là mã dòng vì s0, s1, s2 lặp lại khóa K.
9
Mã dòng (Stream Cipher)
Với mã dòng, các số si được sinh ra phải đảm bảo một độ
ngẫu nhiên nào đó (chu kỳ tuần hoàn dài)
Khóa có chiều dài ngắn: Vigenere => không bảo đảm an toàn
Khóa có chiều dài bằng chiều dài bản tin: One-Time Pad => không thực tế.
Mã dòng cân bằng giữa hai điểm này => khóa ngắn nhưng dãy số sinh ra bảo đảm một độ ngẫu nhiên cần thiết như khóa của One-time Pad, dùng rằng không hoàn toàn thực sự ngẫu nhiên. 10
A5/1
A5/1 được dùng trong mạng điện thoại GSM, để bảo mật dữ liệu trong quá trình liên lạc giữa máy điện thoại và trạm thu phát sóng vô tuyến.
Bộ sinh số mỗi lần sẽ sinh ra hoặc bít 0 hoặc bít 1 để sử dụng
trong phép XOR.
Đơn vị mã hóa của A5/1 là một bít.
11
TinyA5/1
Mô hình thu nhỏ của A5/1 gọi là TinyA5/1.
Cơ chế thực hiện của bộ sinh số TinyA5/1 là như sau:
Thanh ghi X gồm 6 bit, ký hiệu là (x0, x1, …, x5).
Thanh ghi Y gồm 8 bit (y0, y1, …, y7).
Thanh ghi Z lưu 9 bit (z0, z1, …, z8).
Khóa K ban đầu có chiều dài 23 bít và lần lượt được phân bố
vào các thanh ghi: K -> XYZ
Bộ sinh số gồm 3 thanh ghi X, Y, Z.
12
TinyA5/1
Các thanh ghi X, Y, Z được biến đổi theo 3 quy tắc:
13
TinyA5/1
Hàm maj(x, y, z) nếu trong 3 bít x, y, z có từ hai bít 0 trở lên thì hàm trả về giá trị 0, nếu không hàm trả về giá trị 1.
m = maj(x1, y3, z3)
If x1 = m then thực hiện quay X
If y3 = m then thực hiện quay Y
If z3 = m then thực hiện quay Z
Và bít được sinh ra là:
Tại bước sinh số thứ i, các phép tính sau được thực hiện:
trong bản mã theo quy tắc của mã dòng.
Bít si được XOR với bít thứ i trong bản rõ để có được bít thứ i
14
Ví dụ: mã hóa bản rõ P=111 (chữ h) với khóa K là 100101. 01001110.100110000
Mã dòng (Stream Cipher)
15
A5/1
A5/1 hoạt động giống như TinyA5/1.
Kích thước thanh ghi X, Y, Z lần lượt là 19, 22 và 23 bít
16
A5/1
sinh ra là:
Hàm maj được tính trên 3 bít x8, y10, z10. Sau khi quay xong bít
bên dưới:
Toàn bộ quá trình sinh dãy số của A5/1 được minh họa qua hình
17
RC4
RC4 được dùng trong giao thức SSL để bảo mật dữ liệu trong quá trình truyền dữ liệu giữa Web Server và trình duyệt Web.
LAN.
RC4 còn được sử dụng trong mã hóa WEP của mạng Wireless
18
TinyRC4
Là mô hình thu nhỏ của RC4
Đơn vị mã hóa của TinyRC4 là 3 bít.
(từ 0 đến 7).
TinyRC4 dùng 2 mảng S và T mỗi mảng gồm 8 số nguyên 3 bít
Quá trình sinh số của TinyRC4 gồm hai giai đoạn:
Khóa là một dãy gồm N số nguyên 3 bít với N có thể lấy giá trị từ 1 đến 8. Bộ sinh số mỗi lần sinh ra 3 bít để sử dụng trong phép XOR.
19
TinyRC4
a) Giai đoạn khởi tạo
Dãy S gồm các số nguyên 3 bít từ 0 đến 7 được sắp thứ tự tăng dần. Sau đó dựa trên các phần tử của khóa K, các phần tử của S được hoán vị lẫn nhau đến một mức độ ngẫu nhiên nào đó.
20
- Hoán vị S
Ví dụ:
P = 001000110
(từ ‟bag”)
Mã hóa bản rõ:
2, 1, 3 (N=3)
Khóa K gồm 3 số
21
Thực hiện đến khi i=7 và lúc đó dãy S là 6 0 7 1 2 3 5 4
TinyRC4
Các phần tử của S tiếp tục được hoán vị.
b) Giai đoạn sinh số:
Tại mỗi bước sinh số, hai phần tử của dãy S được chọn để tính ra số k 3 bít là số được dùng để XOR với đơn vị mã hóa của bản rõ.
22
- Tiếp tục ví dụ trên, quá trình sinh số mã hóa bản rõ ‟bag” thực hiện:
23
public static int[] cryptRC4(int S[], int T[], int K[], int N) {
// Giai đoạn khởi tạo
for (int i = 0; i < 8; i++) {
S[i] = i;
T[i] = K[i % N];
}
// Hoán vị ngẫu nhiên
System.out.println("Hoán vị mảng S[] ");
int j = 0;
for (int i = 0; i < 8; i++) { j = (j + S[i] + T[i]) % 8;
swap(S, i, j); // Hoán vị S[i] và S[j]
printArrayInt(S, 8);
}
int i = 0;
j = 0;
int k[] = new int[N];
24
int loop = 0;
System.out.println("Giai đoạn sinh số: ");
while (loop < N) {
i = (i + 1) % 8;
j = (j + S[i]) % 8;
swap(S, i, j);
int t = (S[i] + S[j]) % 8;
k[loop] = S[t];
printArrayInt(S, 8);
loop++;
}
return k;
// Chú ý: Phương thức (hàm) này có thể tách ra thành nhiều phương thức nhỏ.
}
25
RC4
đặc tính sau:
Đơn vị mã hóa của RC4 là một byte 8 bít.
Mảng S và T gồm 256 số nguyên 8 bít
Khóa K là một dãy gồm N số nguyên 8 bít với N có thể lấy
giá trị từ 1 đến 256.
Bộ sinh số mỗi lần sinh ra một byte để sử dụng trong phép
XOR.
Cơ chế hoạt động của RC4 cũng giống như TinyRC4 với các
26
RC4
Hai giai đoạn của RC4 là:
đoán trước => RC4 có độ an toàn cao
Quá trình sinh số của RC4 cũng sinh ra dãy số ngẫu nhiên, khó
