Hình học 9 - Chương 5: Đường tròn – Tự luận có lời giải Kết nối trí thức với cuộc sống
Trang 1
CHƯƠNG 5
ĐƯỜNG TRÒN
BÀI 1
MỞ ĐẦU ĐƯỜNG TRÒN
1. Khái niệm đường tròn
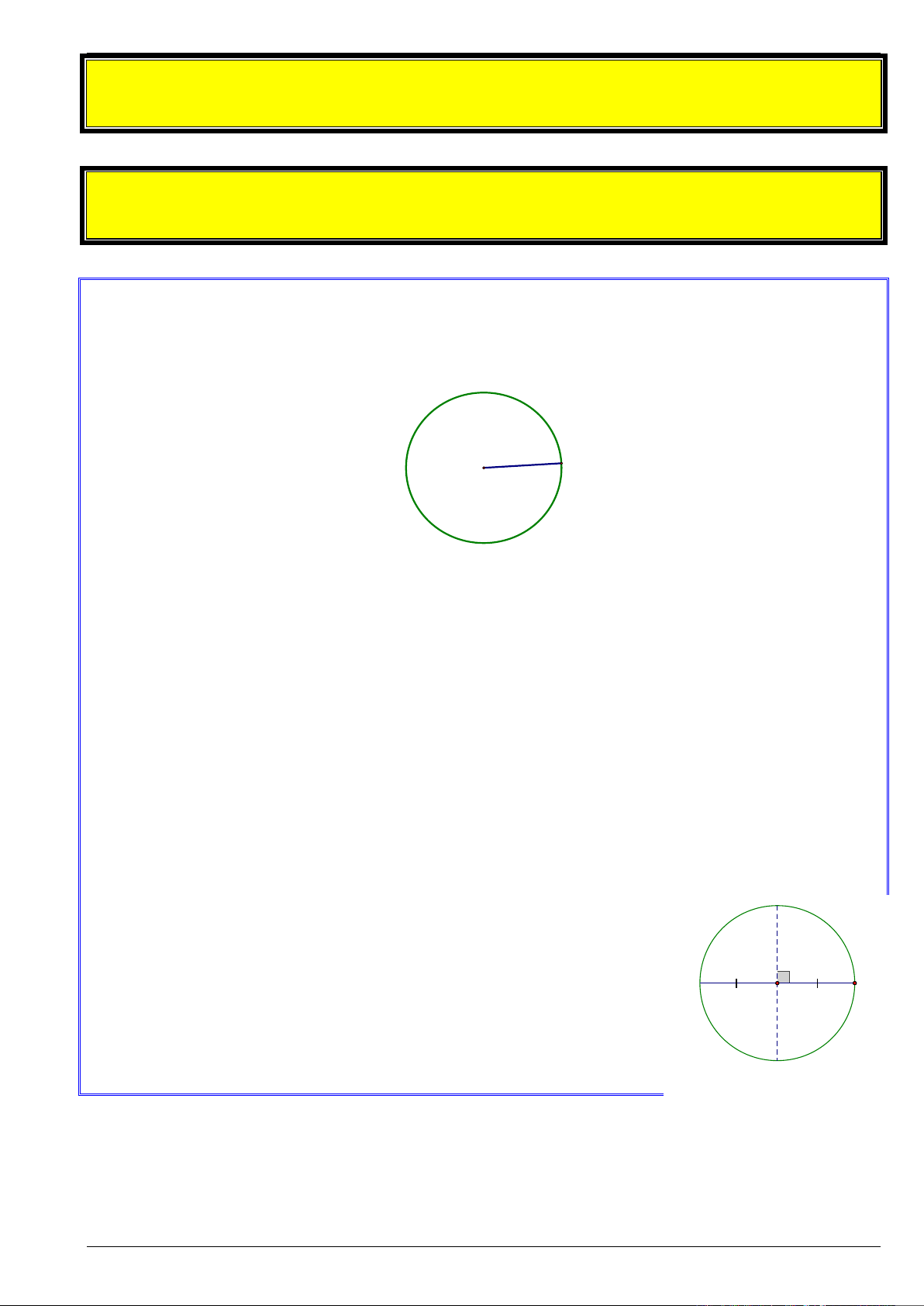
Trong mặt phẳng, đường tròn tâm
O
bán kính
R
(với
0R>
) là tập hợp các điểm cách điểm
O
cố
định một khoảng
R
, kí hiệu là:
( )
;OR
O
R
Chú ý:
• Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
• Khi không chú ý đến bán kính của đường tròn
( )
;OR
, ta cũng có thể kí hiệu đường tròn
( )
O
.
Nhận xét:
• Vị trí tương đối của một điểm đối với đường tròn
+ Điểm
M
nằm trên đường tròn
( )
O
nếu
OM R
=
+ Điểm
M
nằm trong đường tròn
( )
O
nếu
OM R<
+ Điểm
M
nằm ngoài đường tròn
()
O
nếu
OM R
>
• Hình tròn tâm O, bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R)
2. Tính chất đối xứng của đường tròn
• Đường tròn là hình có tâm đối xứng: Tâm của đường tròn là tâm đối
xứng của đường tròn đó
• Đường tròn là hình có trục đối xứng: Bất kì đường kính nào cũng là
trục đối xứng của đường tròn đó.
O
A'
A
Hình học 9 - Chương 5: Đường tròn – Tự luận có lời giải Kết nối trí thức với cuộc sống
Trang 2
CHỨNG MINH CÁC ĐIỂM CHO TRƯỚC CÙNG NẰM TRÊN MỘT ĐƯỜNG TRÒN VÀ
TÍNH BÁN KÍNH ĐƯỜNG TRÒN
Phương pháp
Cách 1: Chứng minh các điểm cho trước cùng cách đều 1 điểm cho trước nào đó.
Cách 2: Nếu
0
90BAC =
thì
A
thuộc đường tròn đường kính
BC
.
C
B
A
O
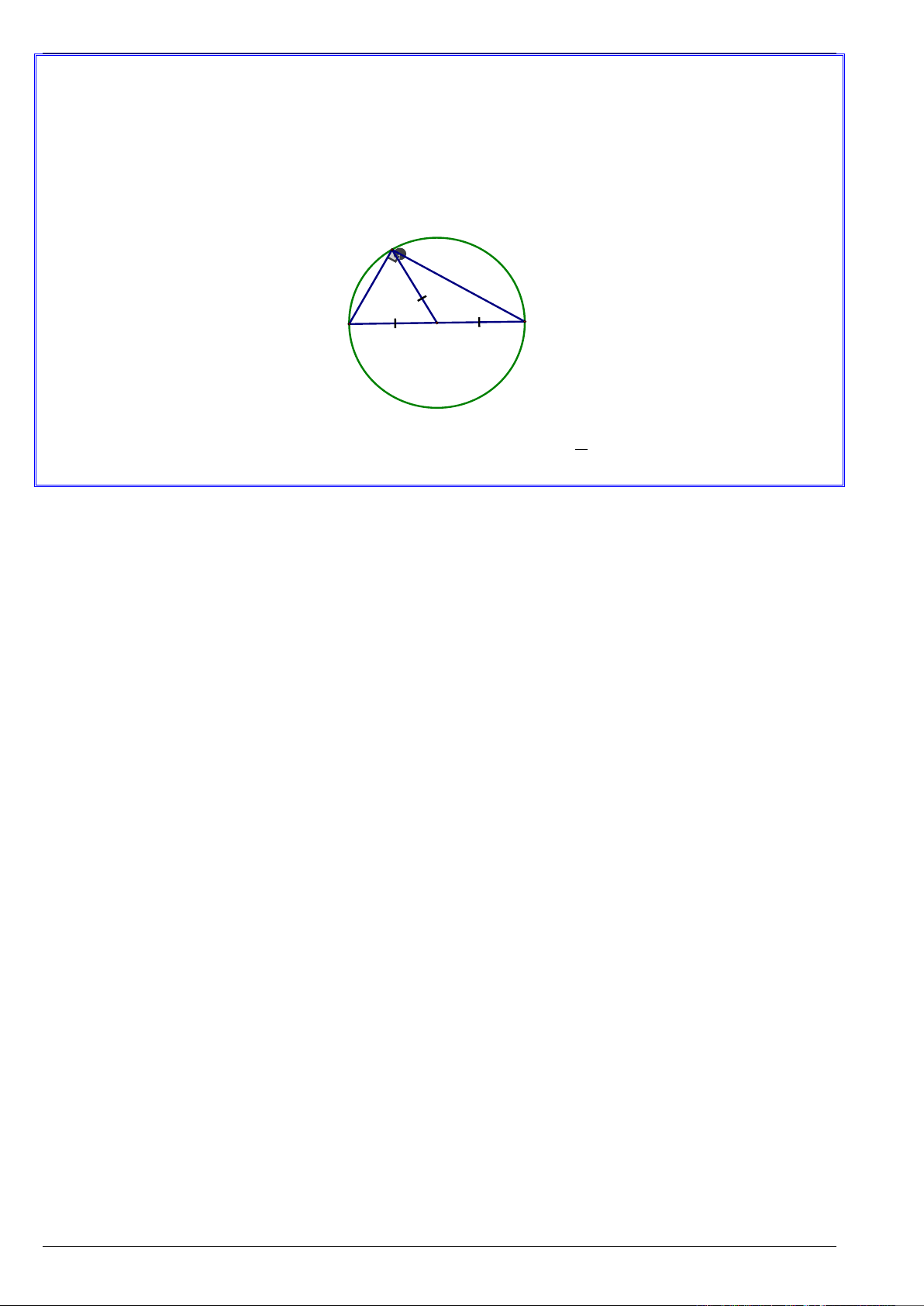
Xét tam giác vuông
ABC
, có
AO
là đường trung tuyến nên
1
2
AO BC AO OB OC= ⇒==
Bài 1. Cho tam giác
ABC
vuông ở
A
có
5 , 12AB cm AC cm= =
.
a) Chứng minh ba điểm
,,ABC
cùng thuộc một đường tròn.
b) Tính bán kính của đường tròn đó.
Bài 2. Cho hình chữ nhật
ABCD
có
9 , 12AB cm BC cm= =
.
a) Chứng minh bốn điểm
,,,ABC D
cùng nằm trên một đường tròn.
b) Tính bán kính đường tròn đó.
Bài 3. Cho tam giác đều
ABC∆
cạnh bằng
a
, các đường cao
,
BM CN
. Gọi
O
là trung điểm của
BC
a) Chứng minh rằng
,, ,BCM N
cùng thuộc đường tròn (O).
b) Gọi
G
là giao điểm của
BM
và
CN
. Chứng minh điểm
G
nằm trong, điểm
A
nằm ngoài đối với
đường tròn đường kính
BC
.
Bài 4. Cho tam giác
( )
0
90ABC A =
, đường cao
AH
. Từ
M
là điểm bất kỳ trên cạnh
BC
. Kẻ
,MD AB ME AC⊥⊥
. Chứng minh 5 điểm
,, ,,ADM H E
cùng nằm trên một đường tròn
Bài 5. Cho đường tròn tâm
( )
O
, đường kính
AB
và một dây
AC
bằng bán kính đường tròn. Tính các
góc của
ABC∆
.
BÀI TẬP RÈN LUYỆN
Bài 6. Cho tam giác đều
ABC
có cạnh bằng
a
.
AM, BN, CP
là các đường trung tuyến. Chứng minh 4
điểm
B,P,N,C
cùng thuộc một đường tròn. Tính bán kính đường tròn đó.
Bài 7. Cho tứ giác
ABCD
có
0
90CD+=
. Gọi
, ,,M N PQ
lần lượt là trung điểm của
,,,AB BD DC CA
.
Chứng minh rằng bốn điểm
, ,,M N PQ
cùng nằm trên 1 đường tròn

Hình học 9 - Chương 5: Đường tròn – Tự luận có lời giải Kết nối trí thức với cuộc sống
Trang 3
Bài 8. Cho hình thoi
ABCD
có
0
60
A=
. Gọi
,,,EFGH
lần lượt là trung điểm của các cạnh
,,,
AB BC CD DA
. Chứng minh rằng 6 điểm
,,, ,,
EFGH BD
cùng nằm trên 1 đường tròn
Bài 9. Cho tam giác
ABC
và điểm
M
là trung điểm của
BC
. Hạ
,
MD ME
theo thứ tự vuông góc với
,AB AC
. Trên tia đối của tia
DB
và
EC
lần lượt lấy các điểm
,IK
sao cho
D
là trung điểm của
BI
,
E
là trung điểm của
CK
. Chứng minh rằng
, ,C,KBI
cùng nằm trên 1 đường tròn.
Bài 10. Gọi
,IK
theo thứ tự là các điểm nằm trên
,AB AD
của hình vuông
ABCD
sao cho
AI AK=
.
Đường thẳng kẻ qua
A
vuông góc với
DI
ở
P
và cắt
BC
ở
Q
. Chứng minh rằng
,,,CDPQ
cùng thuộc
1 đường tròn.
Bài 11. Cho tam giác
ABC
, ba đường cao
,,AD BE CF
cắt nhau tại
H
. Gọi
,, ,IJKL
lần lượt là trung
điểm của
,,,
AB AC HC HB
. Chứng minh rằng 5 điểm
,, ,,,IJ KLEF
thuộc 1 đường tròn.
Bài 12. Cho hình vuông
ABCD
, gọi
O
là giao điểm hai đường chéo
AC
và
BD
. Gọi
,MN
lần lượt là
trung điểm của
,
OB CD
a) Chứng minh rằng
, ,,AM N D
thuộc 1 đường tròn.
b) So sánh
AN
và
DM
.
Bài 13. Cho hình vuông
ABCD
. Gọi
,MN
lần lượt là trung điểm của
,AB BC
. Gọi
E
là giao điểm của
CM
và
DN
a) Tính số đo góc
CEN
b) Chứng minh
,,,ADEM
cùng nằm trên 1 đường tròn
c) Xác định tâm của đường tròn đi qua 3 điểm
,,BDE

Hình học 9 - Chương 5: Đường tròn – Tự luận có lời giải Kết nối trí thức với cuộc sống
Trang 1
CHƯƠNG 5
ĐƯỜNG TRÒN
BÀI 1
MỞ ĐẦU ĐƯỜNG TRÒN
1. Khái niệm đường tròn
Trong mặt phẳng, đường tròn tâm
O
bán kính
R
(với
0R>
) là tập hợp các điểm cách điểm
O
cố
định một khoảng
R
, kí hiệu là:
( )
;OR
O
R
Chú ý:
• Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
• Khi không chú ý đến bán kính của đường tròn
( )
;OR
, ta cũng có thể kí hiệu đường tròn
( )
O
.
Nhận xét:
• Vị trí tương đối của một điểm đối với đường tròn
+ Điểm
M
nằm trên đường tròn
( )
O
nếu
OM R
=
+ Điểm
M
nằm trong đường tròn
( )
O
nếu
OM R<
+ Điểm
M
nằm ngoài đường tròn
()
O
nếu
OM R
>
• Hình tròn tâm O, bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R)
2. Tính chất đối xứng của đường tròn
• Đường tròn là hình có tâm đối xứng: Tâm của đường tròn là tâm đối
xứng của đường tròn đó
• Đường tròn là hình có trục đối xứng: Bất kì đường kính nào cũng là
trục đối xứng của đường tròn đó.
O
A'
A

Hình học 9 - Chương 5: Đường tròn – Tự luận có lời giải Kết nối trí thức với cuộc sống
Trang 2
CHỨNG MINH CÁC ĐIỂM CHO TRƯỚC CÙNG NẰM TRÊN MỘT ĐƯỜNG TRÒN VÀ TÍNH
BÁN KÍNH ĐƯỜNG TRÒN
Phương pháp
Cách 1: Chứng minh các điểm cho trước cùng cách đều 1 điểm cho trước nào đó.
Cách 2: Nếu
0
90BAC =
thì
A
thuộc đường tròn đường kính
BC
.
C
B
A
O
Xét tam giác vuông
ABC
, có
AO
là đường trung tuyến nên
1
2
AO BC AO OB OC= ⇒==
Bài 1. Cho tam giác
ABC
vuông ở
A
có
5 , 12AB cm AC cm= =
.
a) Chứng minh ba điểm
,,ABC
cùng thuộc một đường tròn.
b) Tính bán kính của đường tròn đó.
Lời giải
O
12
5
C
B
A
a) Gọi
O
là trung điểm
BC
Xét tam giác vuông
ABC
, có
AO
là đường trung tuyến nên
1
2
AO BC AO OB OC= ⇒==
Do đó ba điểm
,,ABC
cùng thuộc một đường tròn.
b) Áp dụng định lí Pythagore cho tam giác vuông
ABC
, ta có:
22
13BC AB AC cm= +=
16,5
2
AO OB OC BC cm⇒=== =
Bài 2. Cho hình chữ nhật
ABCD
có
9 , 12AB cm BC cm= =
.
a) Chứng minh bốn điểm
,,,ABCD
cùng nằm trên một đường tròn.



![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)









![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)


