SỞ GD & ĐT HÀ NỘI
TRƯỜNG THPT LƯƠNG THẾ VINH
-----------------------------
ĐỀ THI THỬ ĐẠI HỌC LẦN 2 NĂM 2010
Môn thi: Toán
Thời gian làm bài: 180 phút, không kể thời gian phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu I. (2 điểm)
Cho hàm số
132
24
++−= mmxxy (1) (m là tham s
ố
th
ự
c)
1)
Kh
ả
o sát s
ự
bi
ế
n thiên và v
ẽ
đồ
th
ị
hàm s
ố
(1) khi m = 1.
2)
Tìm các giá tr
ị
c
ủ
a m
để
đồ
th
ị
hàm s
ố
(1) có
đ
i
ể
m c
ự
c
đạ
i và
đ
i
ể
m c
ự
c ti
ể
u,
đồ
ng th
ờ
i các
đ
i
ể
m c
ự
c
đạ
i,
c
ự
c ti
ể
u t
ạ
o thành tam giác có di
ệ
n tích b
ằ
ng 1.
Câu II. (2 điểm)
1)
Gi
ả
i ph
ươ
ng trình:
.xsinxcosxcos 2
4
3
4
3
22
2=
π
−
π
+−
2)
Gi
ả
i h
ệ
ph
ươ
ng trình:
)Ry,x(
)x(y)x(
xxyyx ∈
+=++
+=+
2
6432
112
22
.
Câu III. (1 điểm)
Tính tích phân
∫
π
+
−
=
2
0
12
32 dx
xsin
xcosxsin
I.
Câu IV. (1 điểm)
Cho hình chóp S.ABCD có
đ
áy ABCD là hình ch
ữ
nh
ậ
t, SA vuông góc v
ớ
i m
ặ
t ph
ẳ
ng
đ
áy, SC t
ạ
o v
ớ
i m
ặ
t
ph
ẳ
ng
đ
áy góc 45
0
và t
ạ
o v
ớ
i m
ặ
t ph
ẳ
ng (SAB) góc 30
0
. Bi
ế
t
độ
dài c
ạ
nh AB = a. Tính th
ể
tích kh
ố
i c
ủ
a
chóp S.ABCD.
Câu V. (1 điểm)
Gi
ả
i b
ấ
t ph
ươ
ng trình: 3294
2
12
22
13
−+<
+
+−
++ xx
x
x
.
)Rx(
∈
.
PHẦN RIÊNG (Thí sinh chỉ được làm một trong hai phần: PHẦN A hoặc PHẦN B)
PHẦN A
Câu VIa. (2 điểm)
1) Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trực tâm
);(H 11
−
,
đ
i
ể
m );(E 21
−
là trung
đ
i
ể
m
c
ủ
a c
ạ
nh AC và c
ạ
nh BC có ph
ươ
ng trình 012
=
+
−
yx . Xác
đị
nh t
ọ
a
độ
các
đỉ
nh c
ủ
a tam giác ABC.
2)
Trong không gian v
ớ
i h
ệ
t
ọ
a
độ
Oxyz cho
đườ
ng th
ẳ
ng
2
1
1
1
2
1
1
−
=
+
=
−
∆zyx
:. Vi
ế
t ph
ươ
ng trình m
ặ
t
c
ầ
u (S) có tâm là
đ
i
ể
m );;(I 301 và c
ắ
t
đườ
ng th
ẳ
ng
1
∆
t
ạ
i hai
đ
i
ể
m A, B sao cho tam giác IAB vuông t
ạ
i
I.
Câu VIIa. (1 điểm)
Tìm s
ố
ph
ứ
c z th
ỏ
a mãn:
)iz)(z( 21
+
−
là s
ố
th
ự
c và
z
nh
ỏ
nh
ấ
t.
PHẦN B
Câu VIb. (2 điểm)
1) Trong m
ặ
t ph
ẳ
ng v
ớ
i h
ệ
t
ọ
a
độ
Oxy cho
đ
i
ể
m M(2; 3). Vi
ế
t ph
ươ
ng trình
đườ
ng th
ẳ
ng l
ầ
n l
ượ
t c
ắ
t các tr
ụ
c
Ox, Oy t
ạ
i A và B sao cho MAB là tam giác vuông cân t
ạ
i A.
2)
Trong không gian v
ớ
i h
ệ
t
ọ
a
độ
Oxyz cho
đườ
ng th
ẳ
ng
1
1
1
2
1
1
2
−
+
=
−
=
+
∆zyx
:
. Vi
ế
t ph
ươ
ng trình m
ặ
t
ph
ẳ
ng (P) ch
ứ
a
đườ
ng th
ẳ
ng
2
∆
và t
ạ
o v
ớ
i m
ặ
t ph
ẳ
ng (xOy) m
ộ
t góc nh
ỏ
nh
ấ
t.
Câu VIIb. (1 điểm)
Tìm m
ộ
t acgumen c
ủ
a s
ố
ph
ứ
c
0
≠
z th
ỏ
a mãn zizz =− .
----------
Hết
---------
Họ và tên thí sinh: .................................................................................. Số báo danh .........................................
SỞ GD & ĐT HÀ NỘI
TRƯỜNG THPT LƯƠNG THẾ VINH
--------------------------------
ĐÁP ÁN – THANG ĐIỂM
ĐỀ THI THỬ ĐẠI HỌC LẦN 2 NĂM 2010
Môn thi: Toán
NỘI DUNG ĐIỂM
Câu I. 2 điểm
1) Khảo sát và vẽ đồ thị hàm số 132
24
++−= mmxxy khi m = 1
Khi m = 1 thì 42
24
+−= xxy
* Tập xác định: R
* Sự biến thiên: ⇔=
′
−=
′044
3
y,xxy x = 0; x = -1 hoặc x = 1
* Hàm số đạt cực đại tại x = 0, y
CĐ
= 4; đạt cực tiểu tại
1
±
=
x
, y
CT
= 3
* B
ả
ng bi
ế
n thiên
x
∞
−
-1 0 1
∞
+
y’ - 0 + 0 - 0 +
∞
+
4
∞
+
y
3 3
* V
ẽ
đ
úng
đồ
th
ị
-----------------------------------------------------------------------------------------------------------
2) Tìm các giá trị của m để....................
Ta có 04
2
=−=
′)mx(xy khi x = 0 ho
ặ
c
m
x
=
2
.
Để
hàm s
ố
có C
Đ
, CT thì m > 0.
Khi
đ
ó,
đồ
th
ị
hàm s
ố
có các
đ
i
ể
m C
Đ
, CT là )mm;m(B);m;(A 13130
2
++−−+ và
)mm;m(C 13
2
++−
.
Vì ;OyA
B, C
đố
i x
ứ
ng v
ớ
i nhau qua Oy nên
11
2
1
2
=⇔==−−= mmmxx.yyS
CBBAABC
(th
ỏ
a mãn)
1 điểm
0,25đ
0,25 đ
0,25đ
0,25đ
---------
1 điểm
0,25đ
0,25đ
0,5đ
Câu II.
2 điểm
1) Giải phương trình
.xsinxcosxcos 2
4
3
4
3
22
2
=
π
−
π
+−
Phương trình
( )
22
2
42
2
=π−−
π
+−⇔ xsinxsinxcos
2242
2
=+−⇔ xsinxcosxcos
2222121
22
=++−−⇔ xsinxsinxsin
0222
2
=−+⇔ xsinxsin
22
−
=
⇔
xsin
(lo
ạ
i) ho
ặ
c
1
2
=
x
sin
)Zk(kx ∈π+
π
=⇔
4
-----------------------------------------------------------------------------------------------------------
2)
Giải hệ phương trình:
)Ry,x(
)()x(y)x(
)(xxyyx ∈
+=++
+=+
2112
122
2
6432
.
PTrình (1) 0202
422226322
=+++−⇔=−+−⇔ )xyxyx)(xy()xy()xy(x
2
xy =⇔ do y,xxyxyx ∀>+++ 02
4222
Thay vào phương trình (2) ta được
0112211212
22222
=+−++−+⇔++=++ )]x(x[)xxx(xxx)x(
0121
22
=+−−+⇔ )xx)(x(
1 điểm
0,25đ
0,25đ
0,25đ
0,25đ
----------
1 điểm
0,25đ
0,25đ
0,25đ
*
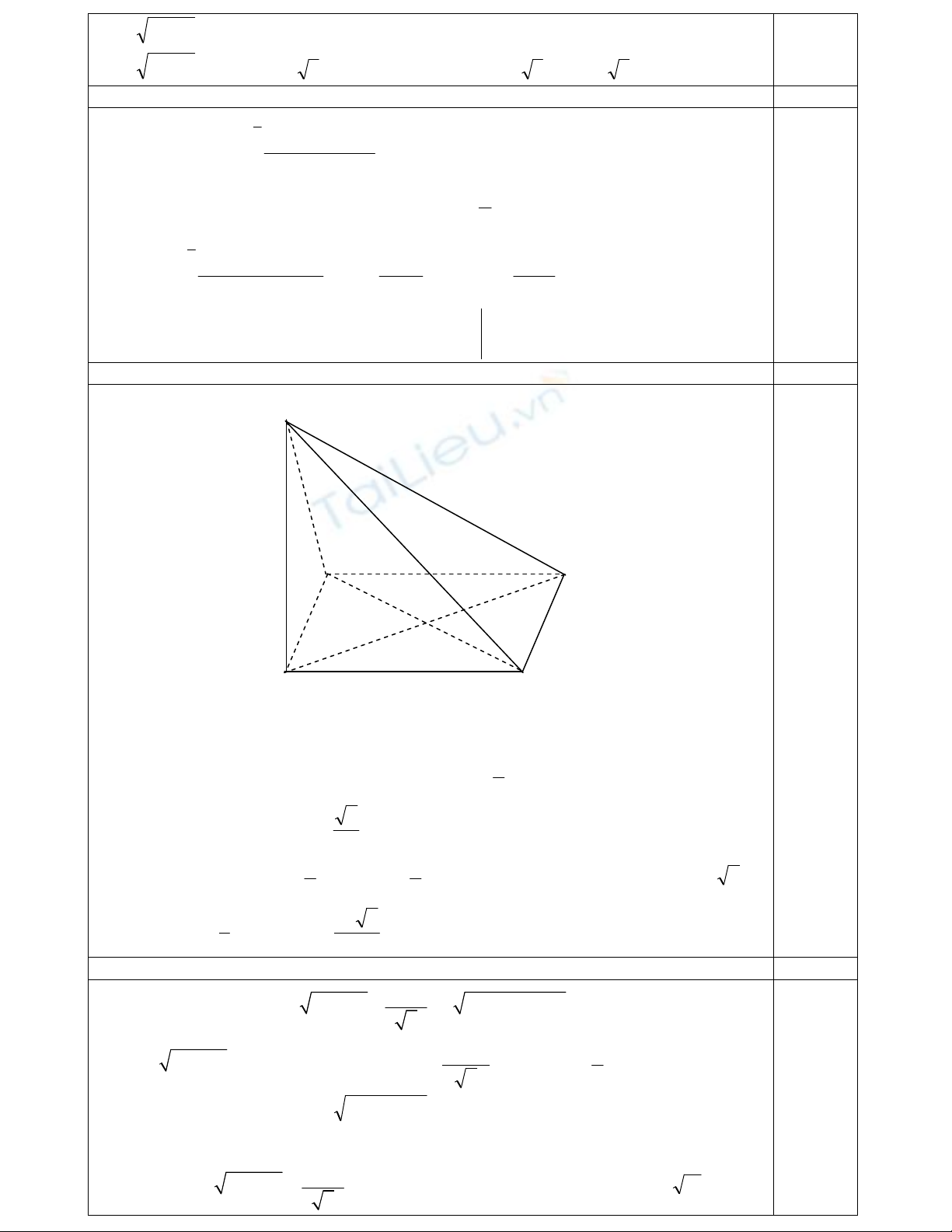
⇒=+ xx 1
2
vô nghiệm
*
321
2
±=⇔=+ xx
.
Vậy hệ có hai nghiệm );( 33− và );( 33
0,25đ
Câu III 1 điểm
Tính tích phân
∫
π
+
−
=
2
0
12
32 dx
xsin
xcosxsin
I.
Đặt t = sinx thì dt = cosxdx và 1
2
00 =
⇒
π
==
⇒
=tx;tx
Ta có:
∫∫
+
−
=
+
−
=
π
1
0
2
0
12
32
12
32 dt
t
t
dx
xsin
xcos)xsin(
I
∫
+
−=
1
0
12
4
1dt
t
[ ]
321
0
1
122 ln)tln(t −=+−=
0,25đ
0,25đ
0,5đ
Câu IV 1 điểm
Tính thể tích khối chóp S.ABCD.
S
D C
O
A a B
Vì )ABCD(SA
⊥
nên
0
45=
∧
SCA ; )SAB(CB
⊥
nên 0
30=
∧
CSB .
Tam giác SBC vuông t
ạ
i B có 0
30=
∧
CSB nên SCBC
2
1
=; Tam giác SAC vuông t
ạ
i A
có 0
45=
∧
SCA nên SCACSA
2
2
== .
Có aBCaSCSCaSCBCABAC =⇔=⇔+=⇔+= 2
4
1
2
1
222222
và
2aSA =
V
ậ
y
3
2
3
1
3
a
S.SAV
ABCDSABCD
==
0,25đ
0,25đ
0,25đ
0,25đ
Câu V 1 điểm
Giải bất phương trình
:
3 1
2 1
2 2 4 9.2 3
2
x
x x x+ +
+
− + < + −
.
Đặ
t
3 2
2 2 0 8.2 2
x x
u u
+
= − ≥ ⇔ = −
và ).(vv xx
x
1224
2
1
0
2
12 2++=⇔>
+
=
Khi
đ
ó bpt tr
ở
thành: 22
22 vuvu +<+
vu)vu(vu)vu( ≠⇔>−⇔+<+⇔ 022 2222
Ta có
3
2 1
2 2
2
x
x
u v
+
+
= ⇔ − =
)(logx. xx 1127052142
2
2±=⇔=+−⇔
0,5đ
0,25đ
V
ậ
y nghi
ệ
m c
ủ
a bpt là
3
2
2
2
2 2 0
log (7 2 11)
log (7 2 11)
x
x
x
x
+
≥ −
− ≥
⇔
≠ ±
≠ ±
0,25đ
Câu VIa 2 điểm
1) Xác định tọa độ các đỉnh của tam giác ABC
.
Gi
ả
s
ử
)m;m(C 12
+
. Vì );(E 21
−
là trung
đ
i
ể
m AC nên A có t
ọ
a
độ
)m;m(A 232
−
−
−
Có )m;m(AH 243 +−+=
→
; );(u
BC
21=
→
.
Vì
BC
AH
⊥
nên
102423 =⇔=+−++=
→→
m)m(mu.AH
BC
. V
ậ
y );(A 13
−
và );(C 31
.
Gi
ả
s
ử
)n;n(B 12
+
. Có );(AC);n;n(BH 24221 =−−−=
→→
. Vì
AC
BH
⊥
nên
0022214 =⇔=−−+−=
→→
n)n()n(AC.BH . V
ậ
y );(B 10 .
-----------------------------------------------------------------------------------------------------------
2) Lập phương trình mặt cầu (S).......
Đườ
ng th
ẳ
ng
1
∆
qua M(1; -1; 1) và có vtcp );;(u 212
=
r
.
Ta có 3
20
240210 1=∆
⇒
−=
−−=
→→
),I(d);;(IM,u);;;(IM
r
G
ọ
i R là bán kính m
ặ
t c
ầ
u.
Để
IAB là tam giác vuông cân t
ạ
i I thì
3
40
21=∆=== ),I(d.IBIAR
V
ậ
y ph
ươ
ng trình m
ặ
t c
ầ
u là
9
40
31 222 =−++− )z(y)x(
1 điểm
0,25đ
0,5đ
0,25đ
----------
1 điểm
0,25đ
0,25đ
0,25đ
0,25đ
Câu VIIa 1 điểm
Tìm số phức z thỏa mãn:
)iz)(z( 21
+
−
là số thực và
z
nhỏ nhất.
Gi
ả
s
ử
z = a + bi ( Rb,a
) thì
[
]
[
]
[
]
[
]
Riba)b(b)a(ai)b(abi)a()iz)(z( ∈−++−−−=−++−=+− 22212121
22
=
+
⇔
ba
Ta có 48522 22222
2+−=−+=+= aa)a(abaz
T
ừ
đ
ó suy ra
z
nh
ỏ
nh
ấ
t khi
5
2
5
4== b;a . V
ậ
y iz
5
2
5
4+=
0,5đ
0,25đ
0,25đ
Câu VIb 2 điểm
1) Viết phương trình đường thẳng ..............
Gi
ả
s
ử
A(a; 0) và B(0; b). Ta có )b;a(BA);;a(MA −=−−=
→→
32
C
ầ
n có
+=+−
=+−
⇔
=
=
→→
222 92
032
0
ba)a(
b)a(a
BAMA
BA.MA
[ ]
−=
=
⇔
−+=+−
−
=
⇔1
3
29
9
92
3
2
2
2
2b
a
)a(
a
)a(
)a(a
b
ho
ặ
c
−=
−=
5
3
b
a
V
ậ
y có hai
đườ
ng th
ẳ
ng th
ỏ
a mãn yêu c
ầ
u là 033
=
−
−
yx và 01535
=
+
+
yx
-----------------------------------------------------------------------------------------------------------
2) Viết phương trình mặt phẳng (P) chứa .........
Gi
ả
s
ử
)c;b;a(n
P
=
→
( )cba 0
222
≠++ .
Vì (P) ch
ứ
a
2
∆
có );;(u 111
2
−=
∆
r
nên 00
2
=−+⇔=
∆
cbau.n
P
r
r
G
ọ
i
α
là góc gi
ữ
a (P) và (xOy). Vì );;(n
)xOy(
100=
r
nên
1 điểm
0,25đ
0,25đ
0,25đ
0,25đ
----------
1 điểm
0,25đ
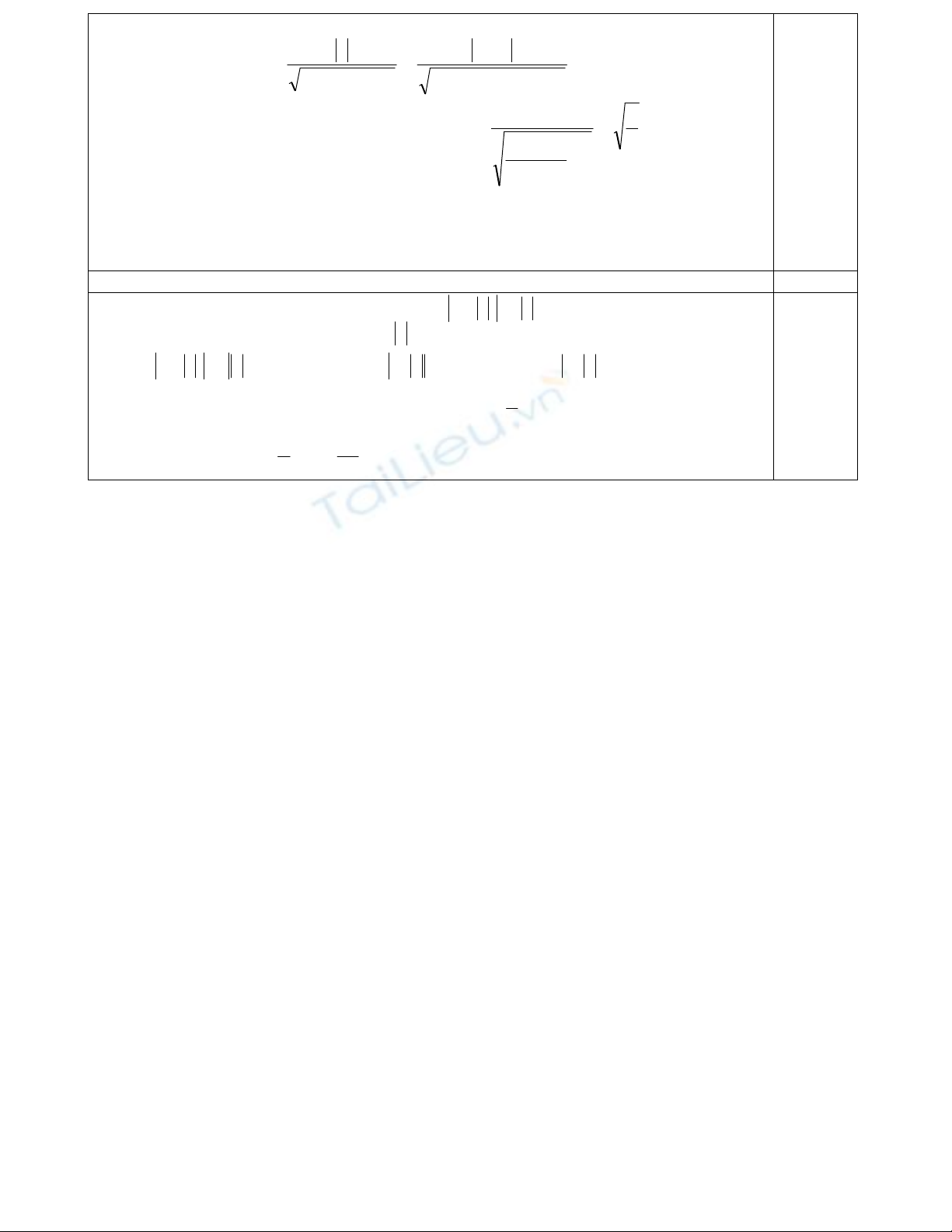
)b,a(f
)ba(ba
ba
cba
c
cos =
+++
+
=
++
=α
222222
Góc
α
nh
ỏ
nh
ấ
t )b,a(f
⇔
l
ớ
n nh
ấ
t. Ta có
3
2
1
1
2
22
≤
+
+
+
=
)ba(
ba
)b,a(f
nên f(a,b) l
ớ
n
nh
ấ
t khi a = b.
Ch
ọ
n a = b = 1 thì c = 2. Vì (P)
đ
i qua
2
121 ∆∈−− );;(M
nên (P) có ph
ươ
ng trình
0120122111
=
+
+
+
⇔
=
+
+
−
+
+
zyx)z()y()x(
0,25đ
0,25đ
0,25đ
Câu VIIb 1 điểm
Tìm một acgumen của số phức
0
≠
z
thỏa mãn
zizz =−
.
Gi
ả
s
ử
α
là m
ộ
t acgumen c
ủ
a z thì
)sini(coszz α+α=
Khi
đ
ó
[
]
z)(sinicosz)(sinicoszizz =−α+α=−α+α=− 11
2
1
11
22
=α⇔=−α+α⇔ sin)(sincos
Vậy z có một acgumen là
6
π
hoặc
6
5
π
.
0,25đ
0,25đ
0,25đ
0,25đ