M C L CỤ Ụ
L I NÓI Đ UỜ Ầ
Với khả năng hi nệ nay, máy tính đã giúp giải được r tấ nhi uề bài toán khó mà trước
đây thường bó tay. M cặ dù v yậ v nẫ có m tộ số lớn các bài toán thú vị mà chưa có
gi iả thu tậ hợp lý để gi iả chúng. Trong đó các bài toán t iố ưu là những bài toán
thường g pặ trong thực ti n.ễ
Bài toán t iố ưu hóa t h pổ ợ có thể xem như bài toán tìm kiếm gi iả pháp t t ốnh tấ
trong không gian vô cùng lớn các gi iả pháp. Khi không gian tìm kiếm nh , ỏnhững
phương pháp cổ đi nể như trên cũng đủ thích hợp, nhưng khi không gian tìm kiếm
lớn ph iả dùng kỹ thu tậ trí tuệ nhân t oạ đ cặ bi t.ệ Thu tậ gi iả di truyền (GA) là m tộ
trong những kỹ thu tậ đó.
Gi i thu t di truy nả ậ ề là m t k thu t c aộ ỹ ậ ủ khoa h c máy tínhọ nh m tìm ki m gi i phápằ ế ả
thích h p cho các bài toán t i u t h p (ợ ố ư ổ ợ combinatorial optimization). Gi i thu t diả ậ
truy n là m t phân ngành c aề ộ ủ gi i thu t ti n hóaả ậ ế v n d ng các nguyên lý c aậ ụ ủ ti nế
hóa như di truy nề, đ t bi nộ ế , ch n l c t nhiênọ ọ ự , và trao đ i chéoổ.
Ngày nay, gi i thu t di truy n đ c dùng ph bi n trong m t s ngành nhả ậ ề ượ ổ ế ộ ố ư tin sinh
h cọ, khoa h c máy tínhọ, trí tu nhân t oệ ạ , tài chính và m t s ngành khác.ộ ố
Bài toán x p ba lôế (m t s sách ghi làộ ố bài toán cái túi) là m t bài toánộ t i u hóa tố ư ổ
h pợ. Bài toán đ c đ t tên t v n đ ch n nh ng gì quan tr ng có th nhét v a vàoượ ặ ừ ấ ề ọ ữ ọ ể ừ
trong m t cái túi (v i gi i h n kh i l ng) đ mang theo trong m t chuy n đi. Cácộ ớ ớ ạ ố ượ ể ộ ế
bài toán t ng t th ng xu t hi n trong kinh doanh,ươ ự ườ ấ ệ toán t h pổ ợ , lý thuy t đ ph cế ộ ứ
t p tính toánạ, m t mã h cậ ọ và toán ng d ngứ ụ .
Chính vì ng d ng l n c a gi i thu t di truy n( GA) và bài toán x p ba lô, v i sứ ụ ớ ủ ả ậ ề ế ớ ự
giúp đ c a th y ỡ ủ ầ Tr n Thanh Hùngầ giáo viên b môn ộGi i thu t di truy n,ả ậ ề chúng
em ti n hành đi tìm hi u v gi i thu t di truy n và ng d ng c a gi i thu t di truy nế ể ề ả ậ ề ứ ụ ủ ả ậ ề
trong bài toán x p ba lô v i đ tài “ế ớ ề Tìm hi u và ng d ng c a thu t gi i di truy nề ứ ụ ủ ậ ả ề
trong bài toán x p ba lô”.ế
Sinh viên th c hi n:ự ệ
Tr n Quang H p.ầ ợ
MSSV: 0441060068.
L p: KHMT1-K4-Đ i h c công nghi p Hà N i(Haui).ớ ạ ọ ệ ộ
Email: hauiquanghop@gmail.com
Môn Gi i thu t di truy n và ng d ng.ả ậ ề ứ ụ
CH NG IƯƠ - T NG QUAN V GI I THU T DI TRUY NỔ Ề Ả Ậ Ề
1. Khái ni mệ
Gi i thu t di truy nả ậ ề là m t k thu t c aộ ỹ ậ ủ khoa h c máy tínhọ nh m tìm ki m gi iằ ế ả
pháp thích h p cho các bài toán t i u t h p (ợ ố ư ổ ợ combinatorial optimization). Gi i thu tả ậ
di truy n là m t phân ngành c aề ộ ủ gi i thu t ti n hóaả ậ ế v n d ng các nguyên lý c aậ ụ ủ ti nế
hóa như di truy nề, đ t bi nộ ế , ch n l c t nhiênọ ọ ự , và trao đ i chéoổ.
Ngày nay, gi i thu t di truy n đ c dùng ph bi n trong m t s ngành nhả ậ ề ượ ổ ế ộ ố ư tin sinh
h cọ, khoa h c máy tínhọ, trí tu nhân t oệ ạ , tài chính và m t s ngành khác.ộ ố
Tư tưởng c aủ thu tậ toán di truy nề là mô phỏng các hi nệ tượng tự nhiên: K ếthừa
và đ uấ tranh sinh t nồ đ cáiể ti nế lời gi iả và kh oả sát không gian lời gi iả khái ni mệ
kế thừa và đ uấ tranh sinh t nồ được gi iả thích qua thí dụ về sự ti nế hóa c a ủm tộ
qu nầ thể thỏ như sau:
Có m tộ qu nầ thể th ,ỏ trong đó có m tộ số con nhanh nh nẹ và thông minh hơn những
con khác. Những chú thỏ nhanh nh nẹ và thông minh có xác su tấ bị ch n cáoồ ăn th tị
nhỏ hơn, do đó cũng t nồ t iạ dể làm những gì t tố nh tấ có thể : T o ạthêm nhi uề
thỏ t t.ố Dĩ nhiên, m tộ số thỏ chậm ch pạ đ nầ đ nộ cũng sống sót vì may m n.ắ
Qu nầ thể những chú thỏ còn sống sót sẽ b tắ đ uầ sinh s n.ả Vi cệ sinh s nả này sẽ
t oạ ra m tộ h nỗ hợp t tố về "nguyên li uệ di truy nề thỏ". M tộ số th ỏch mậ ch pạ có
con với những con thỏ nhanh, m tộ số nhanh nh nẹ có con với th ỏnhanh nh n,ẹ một
số thông minh với thỏ đ nầ đ n… ộVà trên t tấ cả thiên nhiên l i ạném vào m tộ con thỏ
"hoang dã" bằng cách làm đ tộ bi nế nguyên li uệ di truy n ềth .ỏ Những chú thỏ con do
k tế quả này sẽ nhanh hơn và thông minh hơn những con thỏ trong quần thể g cố vì
có nhi uề bố mẹ nhanh nh nẹ và thông minh hơn đã thoát ch tế kh iỏ ch nồ cáo.
Khi tìm ki mế lời gi iả t iố ưu , thu t toánậ di truy nề cũng thực hi nệ các bước tương
ứng với câu chuy nệ đ uấ tranh sinh t nồ c aủ loài th .ỏ
Thu tậ toán di truy nề sử dụng các thu tậ ngữ vay mượn c aủ di truy nề h c.ọ Ta có thể
nói về các cá thể (hay ki uể gen, c uấ trúc) trong m tộ qu nầ th ,ể những cá thể này
cũng còn được g iọ là chu iỗ hay các nhi mễ s cắ thể.
M iỗ ki uể gen (ta g iọ là m tộ nhiễm s cắ th )ể sẽ bi uể di nễ m tộ lời gi iả c aủ bài toán
đang gi iả (ý tưởng c aủ m tộ nhiễm s cắ thể cụ thể được người sử dụng xác đ nhị
trước), m tộ tiến trình ti nế hóa được thực hi nệ trên m tộ qu n ầthể các nhiễm s cắ thể
tương ứng với m tộ quá trình tìm kiếm lời gi iả trong không gian lời giải. Tìm kiếm
đó cần cân đ iố hai m cụ tiêu: Khai thác những lời gi iả t tố nh tấ và kh o ảsát không
gian tìm kiếm. Leo đ iồ là m tộ ví dụ về chi nế lược cho phép khai thác và c iả thi nệ
lời gi iả t tố nh tấ hi nệ hành nhưng leo đ iồ l iạ bỏ qua vi cệ kh oả sát không gian tìm
kiếm. Ngược l i,ạ tìm kiếm ngẫu nhiên là m tộ ví dụ đi nể hình c a ủchi nế lược kh oả
sát không gian tìm kiếm mà không chú ý đ nế vi cệ khai thác những vùng đ yầ hứa
h nẹ c aủ không gian. Thu tậ toán di truy nề (GA) là phương pháp tìm kiếm (đ cộ lập
mi n)ề t oạ được sự cân đ iố đáng kể giữa vi cệ khai thác và kh oả sát không gian tìm
kiếm.
Thực ra, GA thu cộ lớp các thu tậ gi iả xu tấ s c,ắ nhưng l iạ r tấ khác những thu t ậgi iả
ng uẫ nhiên vì chúng k tế hợp các ph nầ tử tìm kiếm trực ti pế và ng uẫ nhiên. Khác
bi tệ quan trọng giữa tìm kiếm c aủ GA và các phương pháp tìm kiếm khác là GA
duy trì và xử lý m tộ tập các lời gi iả (ta g iọ là m tộ qu nầ th )ể
Theo đề xu tấ c aủ giáo sư John Holland, m tộ v nấ đề bài toán đ tặ ra s đẽ ược mã hóa
thành các chu iỗ với chi uề dài bit cố đ nh.ị Nói m tộ cách chính xác là các thông số
c aủ bài toán sẽ được chuy nể đ iổ và bi uể di nễ l iạ dưới dạng các chu iỗ nhị phân.
Các thông số này có thể là các bi nế c aủ m tộ hàm ho cặ hệ số của m tộ bi uể thức
toán h c.ọ Người ta g iọ các chu iỗ bít này là mã genome ứng với m iỗ cá th ,ể các
genome đ uề có cùng chi uề dài. Nói ngắn g n,ọ m tộ lời gi iả s đẽ ược bi uể diễn
bằng m tộ chu iỗ bít, cũng như m iỗ cá thể đ uề được quy định bằng gen c aủ cá thể đó
v y.ậ Như v y,ậ đ iố với thuật gi iả di truy n,ề m tộ cá thể chỉ có m tộ gen duy nh tấ và
m tọ gen cũng chỉ ph cụ vụ cho m tộ cá thể duy nhât. Do đó, gen chính là cá thể và cá
thể chính là gen.
Ban đ u,ầ ta sẽ phát sinh m tộ số lượng lớn, giới h nạ các cá thể có gen ngẫu nhiên -
nghĩa là phát sinh m tộ t pậ hợp các chu i bitỗ ng uẫ nhiên. T pậ các cá th nàyể được
g iọ là qu nầ thể ban đ uầ (initial population). Sau đó, dựa trên m tộ hàm nào đó, ta sẽ
xác đ nhị được m tộ giá trị có độ thích nghi - Fitness. Giá trị này, đ để ơn gi nả cho đơn
gi nả chính là độ "t t"ố c aủ lời gi iả hay đọ cao trong tìm kiếm theo ki uể leo đ i. ồVì
phát sinh ng uẫ nhiên nên độ "t t"ố c aủ lời gi iả hay tính thích nghi c aủ cá thể trong
qu nầ thể ban đ uầ là không xác đ nh.ị
Để c iả thi nệ tính thích nghi c aủ qu nầ thể người ta tìm cách t oạ ra qu nầ th ểmới. Có
hai cách thao tác thực hi nệ trên thế hệ hi nệ t iạ để t o raạ m tộ thế hệ khác với độ
thích nghi t tố hơn.
Thao tác đ uầ tiên là sao chép nguyên m uẫ một nhóm các cá thể t tố từ thế h trệ ước
r iồ đưa sang thế hệ sau (selection). Thao tác này đảm b oả độ thích nghi c aủ thế
hệ sau luôn được giữ ở m tộ mức độ hợp lý. Các cá thể được ch nọ thông thường là
các cá thể có độ thích nghi cao nh t.ấ
Thao tác thứ hai là t oạ ra cá thể mới b nằg cách thực hi nệ các thao tác sinh s nả
trên m tộ s cá thố ể được ch nọ từ thế h tệrước, thông thường cũng là những cá thể có
độ thích cao. Có hai lo iạ thao tác sinh s n:ả m tộ là thao tác lai t o ạ(crossover), hai là
đ tộ bi nế (mutalion). Trong thao tác lai t o,ạ từ gen c aủ hai cá thể được ch nọ trong
thế hệ trước sẽ được phối hợp với nhau (theo m tộ quy tác nào đó) đ t oể ạ thành hai
gen mới.
Thao tác chọn l cọ và lai t oạ giúp t oạ ra thế hệ sau. Tuy nhiên, nhi uề khi do thế hệ
khởi t oạ ban đ uầ có đ cặ tính chưa phong phú và chưa phù hợp nên các cá thể không
r iả đ uề được không gian c aủ bài toán (tương tự như trường hợp leo đ i,ồ các người
leo đ iồ t pậ trung d nồ vào m tộ góc trên vùng đ t).ấ Từ đó, khó có thể tìm ra lời gi iả
t iố ưu cho bài toán. Thao tác đ tộ bi nế sẽ giúp gi iả quy tế được v nấ đề này. Đó là
sự bi nế đ iổ ng uẫ nhiên m tộ ho cặ nhi uề thành ph nầ gen c a ủm tộ cá thể ở thế hệ
trước t oạ ra m tộ cá thể hoàn toàn mới ở thế hệ sau. Nhưng thao tác này chỉ được
phép xảy ra với t nầ su tấ r tấ th pấ (thường dưới 0.01), vì thao tác này có thể gây
xáo tr nộ và làm m tấ đi những cá thể ch nọ l cọ và lai t o ạcó tính thích nghi cao, d nẫ
đ nế thu tậ toán không còn hi uệ qu .ả
Thế h ệmới được t oạ ra l iạ được xử lý như thế h tệrước cho đ nế khi có m tộ cá thể
đ tạ được gi iả pháp mong mu nố ho cặ đ tạ đ nế thời gian giới h nạ
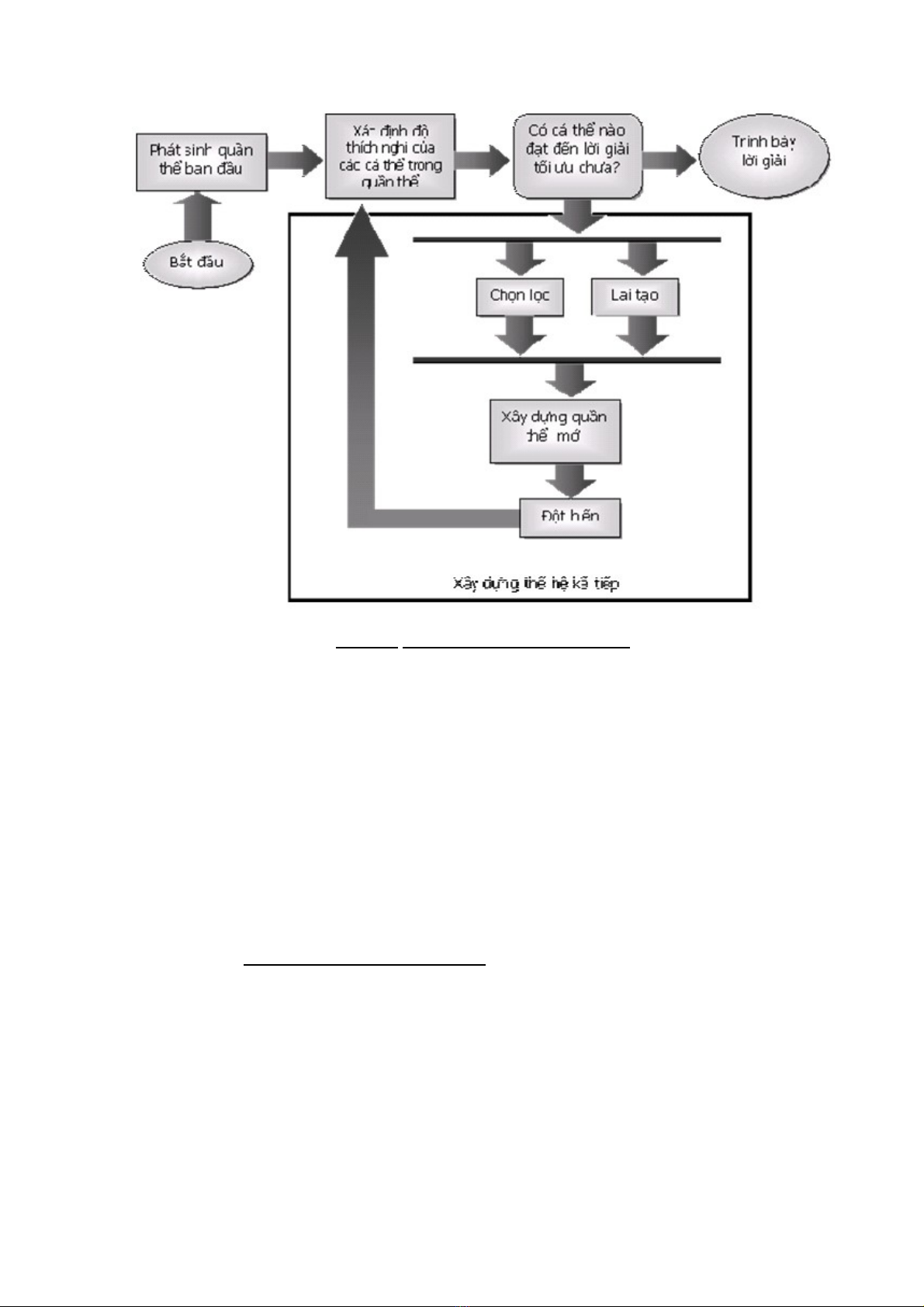
Hình 1. S đ gi i thu t di truy nơ ồ ả ậ ề
C uấ trúc c aủ gi iả thu tậ di truy nề như sau:
T=0
Initialize P(t)
evaluate structures in P(t)
While not end do
T= t + 1
Select C(t) from P(t - 1)
Recombine structures in C(t) forming C'(t)
Mutate structures in C' (t) forming C'' (t)
Evaluate structures in C''(t)
Replace P(t) from C''(t) and/or P (t - 1)
2. Các b c c a gi i thu t di truy nướ ủ ả ậ ề
2.1. Kh i t o qu n th ở ạ ầ ể (initialize )
Qu nầ thể đ uầ tiên được khởi t oạ m tộ cách ngẫu nhiên từ t pậ hợp những cá thể
riêng l .ẻ Kích cỡ c aủ qu nầ thể đ uầ tiên phụ thuộc vào y uế tố tự nhiên c aủ bài toán,
nhưng nhìn chung thì m tộ bài toán có đ nế hàng trăm hay hàng nghìn gi iả pháp hợp lý.
T pậ hợp những gi iả pháp hợp lý cho v n đấ ề được g iọ là không gian tìm ki mế
(search space). Trước m tộ bài toán áp d ng ụthu tậ toán di truy n,ề ta c nầ ph iả xác đ nhị
rõ nhi m s cễ ắ thể và cá thể cho v nấ đ , ềvà thông thường đó sẽ là k tế quả cu iố
cùng. Vi cệ phân tích sẽ dựa trên k tế qu cả ơ b nả t tố nhất.
Ví d : ụ
v1: 1 0 0 0 1 1 1