Đ 1ỀĐ KI M TRA H C K IỀ Ể Ọ Ỳ
Môn TOÁN L P 9Ớ
Th i gian: 90 phútờ
Câu 1. (3đi m).ể
a)Tính giá tr c a bi u th c A và B:ị ủ ể ứ
A = B=
b) Rút g n bi u th c :.ọ ể ứ
c) Ch ng minh r ng giá tr c a bi u th c sau không ph thu c vào giá tr c a a:ứ ằ ị ủ ể ứ ụ ộ ị ủ
v i ớ
Câu 2. (2,0 đi m).ể Cho hàm s y = ax -2 có đ th là đng th ng ố ồ ị ườ ẳ
a) Bi t đ th hàm s qua đi m A(1;0). Tìm h s a, hàm s đã cho là đng bi n hay ngh chế ồ ị ố ể ệ ố ố ồ ế ị
bi n trên R? Vì sao? ế
b) V đ th hàm s v a tìm đc.ẽ ồ ị ố ừ ượ
c) V i giá tr nào c a m đ đng th ng : y=(m-1)x+3 song song ?ớ ị ủ ể ườ ẳ
Câu 3.(2,0đi m)ể.Cho tam giác ABC, đng cao AH, bi t AB = 30cm, AC = 40cm, ườ ế
BC = 50cm.
a) Ch ng minh tam giác ABC vuông t i Aứ ạ
b) Tính đng cao AH?ườ
c) Tính di n tích tam giác AHC?ệ
Câu 4 . (2,5 đi mể). Cho đng tròn (O; 6cm), đi m A n m bên ngoài đng tròn, ườ ể ằ ườ
OA = 12cm. K các ti p tuy n AB và AC v i đng tròn (B, C là các ti p đi m).ẻ ế ế ớ ườ ế ể
a) Ch ng minh BC vuông góc v i OA.ứ ớ
b) K đng kính BD, ch ng minh OA // CD.ẻ ườ ứ
c) G i K là giao đi m c a AO v i BC. Tính tích: OK.OA =? Vaø tính ?ọ ể ủ ớ
Câu 5.(0,5đi m).ểTìm giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
-------------------(H t)-----------------ế
ĐÁP ÁN
CâuÝĐáp ánĐi mể
1
Câu 1
(3đi m)ể
a
0,25
0,25
0,25
0,25
0,25
b
0,25
0,25
0,25
0,25
c v i ớ
0,25
0,25
V y M không ph thu c vào a.ậ ụ ộ 0,25
Câu 2
(2đi m)ể
aĐ th hàm s y = ax -2 qua đi m A(1;0) ta cóồ ị ố ể : 0 = a.1-2 => a=2 0,25
V y hàm s đó làậ ố :y = 2x-2
Hàm s đng bi n trên R, vì a = 2 > 0ố ồ ế 0,25
b B ng giá tr t ng ng x và y:ả ị ươ ứ
x 0 1
y= 2x-2 -2 0
0,25
V đ th :ẽ ồ ị
y
=2x-2
x
y
-2
2
O
1
0.75
cĐ đng th ng dể ườ ẳ 2//d1 thì m - 1 = 2 => m = 3 0.5
2
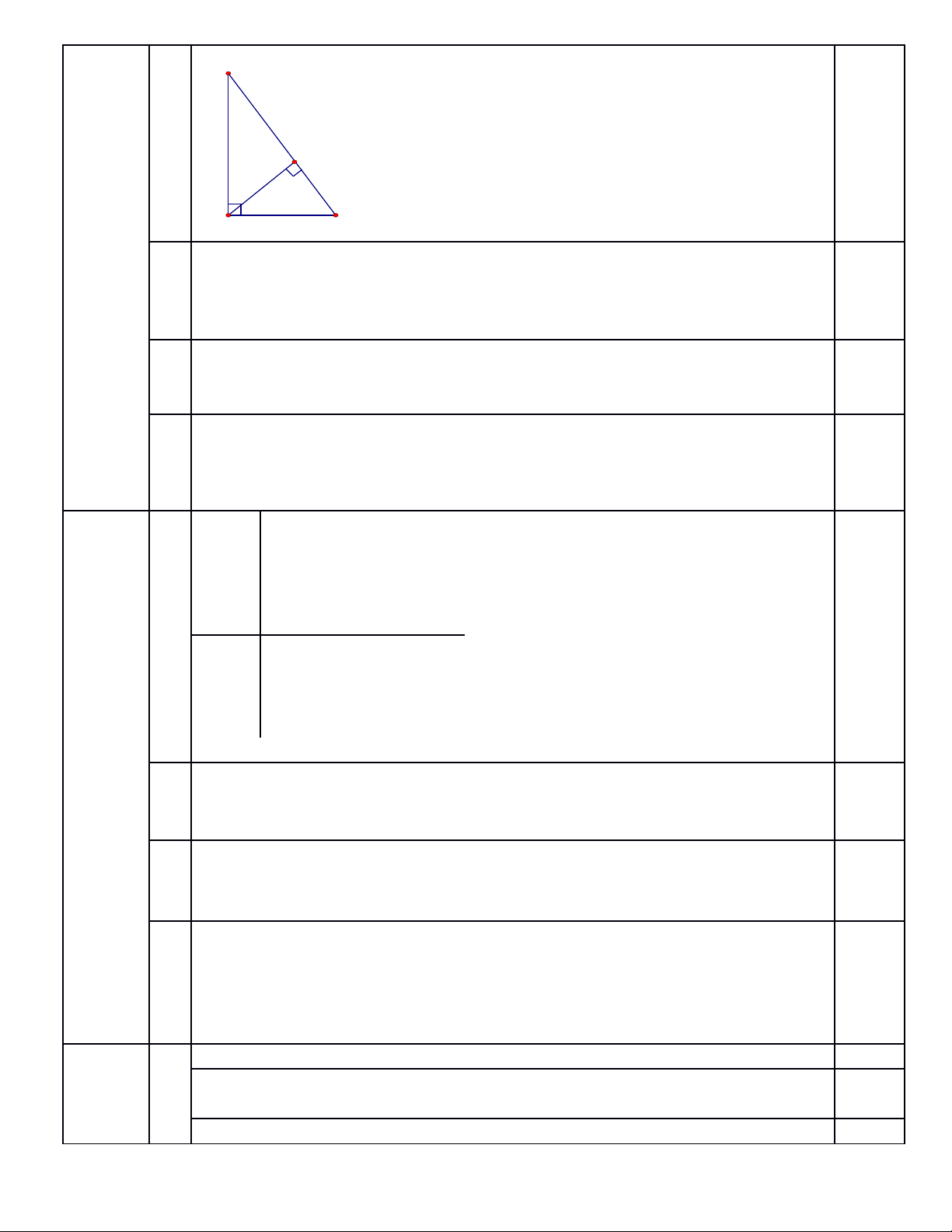
Câu 3
(2.0đi mể
)
A
B
C
H
a Ta có: BC2 = 502 = 2500,
AB2 + AC2 = 302 + 402 = 2500
BC2 = AB2 + AC2, v y tam giác ABC vuông t i A.(Đnh lý đo Py –ta – ậ ạ ị ả
go)
0.25
0,25
0.25
b Ta có: BC . AH = AB . AC (H th c l ng trong tam giác vuông)ệ ứ ượ
50 . AH = 30 . 40
24 (cm)
0.25
0.25
0.25
c Ap d ng ụh th c gi a c nh góc vuông và hình chi u c a nó trên c nh huy n ta ệ ứ ữ ạ ế ủ ạ ề
có :
AC2 = BC.HC HC = = = 32(cm)
*
0.25
0.25
Câu 4:
(2,5đi m)ể
GT
Cho (O ; 6cm), A
(O)
OA = 12 cm, k hai ttẻ
AB và AC (B,C ti pế
đi m) ểđng kính BDườ
KL
a) BC OA.
b) OA // CD.
c) OK.OA =?
= ?
0,25
a
Ta có: ABC cân t i A ( AB = AC – T/c hai ti p tuy n c t nhau)ạ ế ế ắ
AO là tia phân giác c a góc A (T/c hai ti p tuy n c t nhau)ủ ế ế ắ
=> AO cũng là ®êng cao hay : AO BC.
0.25
0.25
0.25
bBCD vu«ng t¹i C(OC trung tuy n tam giác BCD, OC= BD) ế
nªn CD BC .
L¹i cã: AO BC ( cmt). => AO // CD
0,25
0.25
0.25
cABO vuông t i B, có BK là đng caoạ ườ
=> OK.OA = OB2 = 62 = 36
Ta có sin BAO =
=> =300
0.25
0.25
0,25
Câu 5
(0,5đi mể0,25
Bi u th c A đt giá nh nh t là 2 khi và ch khi ể ứ ạ ỏ ấ ỉ
3
)Hay x – 2 = 0 suy ra x = 2 0,25
( L u ý: H c sinh gi i cách khác đúng v n đc đi m t i đa)ư ọ ả ẫ ượ ể ố
Đ 2ỀĐ KI M TRA H C K IỀ Ể Ọ Ỳ
Môn TOÁN L P 9Ớ
Th i gian: 90 phútờ
I PH N TR C NGHI M KHÁCH QUAN: Ầ Ắ Ệ (4 ®iÓm)
Câu 1.Căn b c hai s h c c a 9 làậ ố ọ ủ
A. -3. B. 3. C. 81. D. -81.
Câu 2.Bi u th c xác đnh khi:ể ứ ị
A. . B. . C. . D. .
Câu 3.Cho ∆ABC vuông t i A, AH là đng cao ạ ườ (h.1). Khi đó đ dài AH b ngộ ằ
A. 6,5. B.6
h.2
A
B
h.1
9
4
B
A
C. 5. D. 4,5.
Câu 4.Trong hình 2, cosC b ngằ
A. . B. . C. . D. .
Câu 5.Bi u th c b ngể ứ ằ
A. 3 – 2x. B. 2x – 3. C. .D. 3 – 2x và 2x – 3.
Câu 6.Giá tr c a bi u th c b ngị ủ ể ứ ằ
A. 1. B. 2. C. 3. D. 0.
Câu 7.Giá tr c a bi u th c b ngị ủ ể ứ ằ
A. . B. 1. C. -4. D. 4.
Câu 8.Cho tam giác ABC vuông t i A có AB = 18; AC = 24. Bán kính đng tròn ngo i ti p tam giác ạ ườ ạ ế
đó b ngằ
4
A. 30. B. 20. C. 15. D. 15.
Câu 9.Trong các hàm s sau, hàm s nào là hàm s b c nh t ?ố ố ố ậ ấ
A. . B. . C. . D. .
Câu 10.Trong các hàm s sau, hàm s nào đng bi n ?ố ố ồ ế
A. y = 2 – x
B. C. . D. y = 6 – 3(x – 1).
Câu 11.Đi m nào trong các đi m sau thu c đ th hàm s y = 1 – 2x ?ể ể ộ ồ ị ố
A. (-2; -3). B. (-2; 5). C. (0; 0). D. (2; 5).
Câu 12.N u hai đng th ng y = -3x + 4 (dế ườ ẳ 1) và y = (m+1)x + m (d2) song song v i nhau thì m b ngớ ằ
A. – 2. B. 3. C. - 4. D. – 3.
Câu 13.M t đng th ng đi qua đi m A(0; 4) và song song v i đng th ng x – 3y = 7 có ph ng ộ ườ ẳ ể ớ ườ ẳ ươ
trình là
A. .
B. y = - 3x + 4.
C. .
D. y = - 3x – 4.
Câu 14.Cho tam giác DEF có DE = 3; DF = 4; EF = 5. Khi đó
A.DE là ti p tuy n c a (F; 3).ế ế ủ B.DF là ti p tuy n c a (E; 3).ế ế ủ
C.DE là ti p tuy n c a (E; 4).ế ế ủ D.DF là ti p tuy n c a (F; 4).ế ế ủ
Câu 15.Cho hai đng th ng (dườ ẳ 1) và (d2) nh hình v . Đng th ng (dư ẽ ườ ẳ 2) có ph ng trình làươ
A. y = - x.
B. y = - x + 4.
C. y = x + 4.
5