zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Đề thi - Kiểm tra

Tuyển tập đề thi vào lớp 10 môn Toán năm 2013-2014 các tỉnh

Chia sẻ: Nguyễn Bảo Giang | Ngày: | Loại File: PDF | Số trang:8

Báo xấu

1.127
lượt xem 392
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tuyển tập đề thi vào lớp 10 môn Toán năm 2013-2014 các tỉnh nhằm giúp cho học sinh ôn tập, luyện tập và vận dụng các kiến thức vào việc giải các bài tập và đặc biệt khi giải những bài tập cần phải tính toán một cách nhanh nhất, thuận lợi nhất. Mời các em tham khảo tài liệu để nắm vững hơn nội dung kiến thức cũng như cấu trúc đề thi.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tuyển tập đề thi vào lớp 10 môn Toán năm 2013-2014 các tỉnh

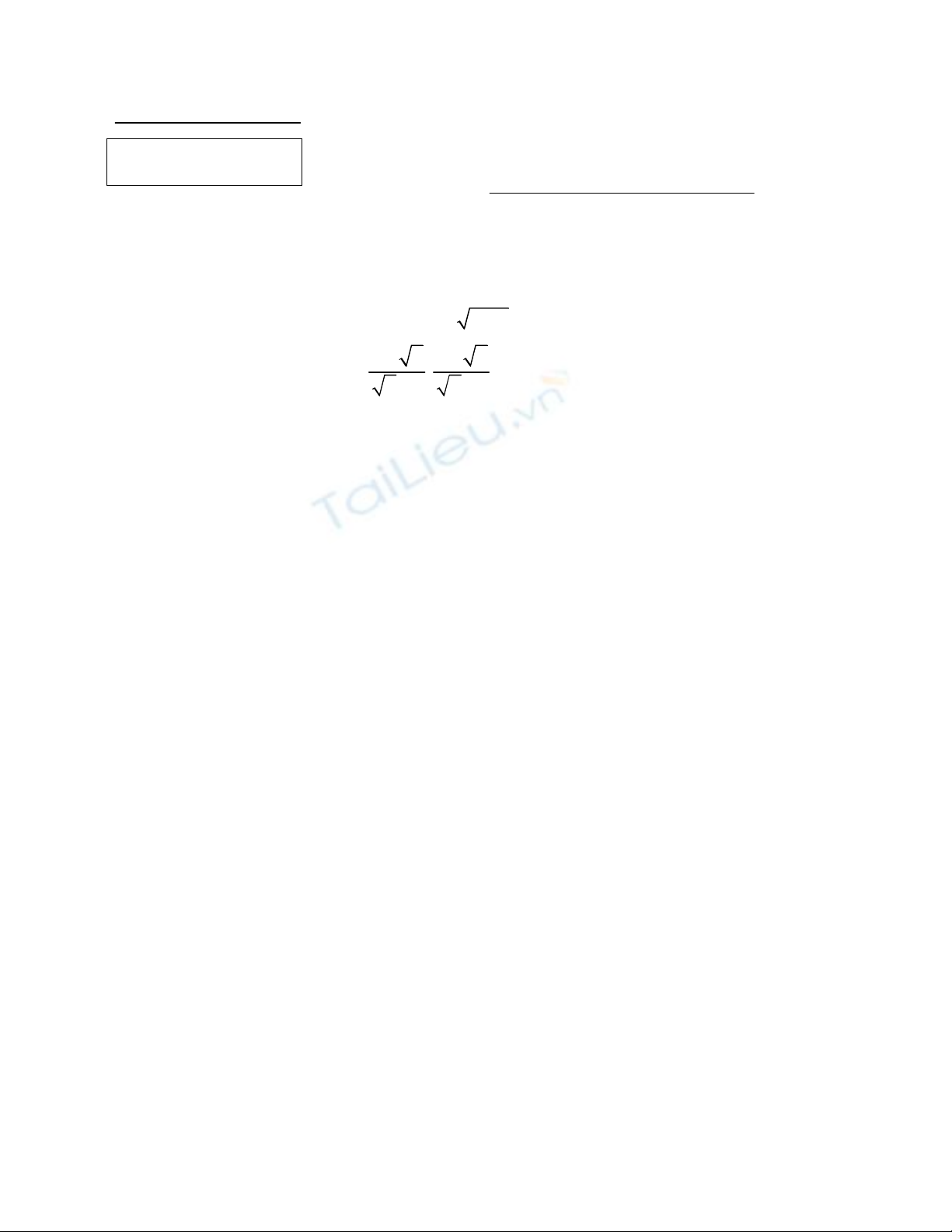
www.VNMATH.com UBND TỈNH BẮC NINH ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2013 – 2014 Môn thi: Toán (Dành cho tất cả thí sinh) ĐỀ CHÍNH THỨC Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Ngày thi: 20 tháng 6 năm 2013 Câu 1. (2,0 điểm) a) Giải phương trình: 2 x  3  0. b) Với giá trị nào của x thì biểu thức x  5 xác định? c) Rút gọn biểu thức: A  2  2 . 2  2 . 2 1 2 1 Câu 2. (2,0 điểm) Cho hàm số: y  mx  1 (1), trong đó m là tham số. a) Tìm m để đồ thị hàm số (1) đi qua điểm A(1;4) . Với giá trị m vừa tìm được, hàm số (1) đồng biến hay nghịch biến trên  ? b) Tìm m để đồ thị hàm số (1) song song với đường thẳng d: y  m 2 x  m  1. Câu 3. (1,5 điểm) Một người đi xe đạp từ A đến B cách nhau 36 km. Khi đi từ B trở về A, người đó tăng vận tốc thêm 3 km/h, vì vậy thời gian về ít hơn thời gian đi là 36 phút. Tính vận tốc của người đi xe đạp khi đi từ A đến B. Câu 4. (3,0 điểm) Cho nửa đường tròn đường kính BC, trên nửa đường tròn lấy điểm A (khác B và C). Kẻ AH vuông góc với BC (H thuộc BC). Trên cung AC lấy điểm D bất kì (khác A và C), đường thẳng BD cắt AH tại I. Chứng minh rằng: a) IHCD là tứ giác nội tiếp; b) AB2 = BI.BD; c) Tâm đường tròn ngoại tiếp tam giác AID luôn nằm trên một đường thẳng cố định khi D thay đổi trên cung AC. Câu 5. (1,5 điểm) a) Tìm tất cả các bộ số nguyên dương ( x; y ) thỏa mãn phương trình: x 2  2 y 2  3 xy  2 x  4 y  3  0.   b) Cho tứ giác lồi ABCD có BAD và BCD là các góc tù. Chứng minh rằng AC  BD. ------------Hết------------ (Đề này gồm có 01 trang) Họ và tên thí sinh: ……………………………..……Số báo danh: ……………….....
www.VNMATH.com UBND TỈNH BẮC NINH HƯỚNG DẪN CHẤM SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN NĂM HỌC 2013 – 2014 Môn thi: Toán (Dành cho tất cả thí sinh) Câu Lời giải sơ lược Điểm 1 a) (0,5 điểm) (2,0 điểm) Ta có 2 x  3 0,25 3 x 0,25 2 b) (0,5 điểm) x  5 xác định khi x  5  0 0,25  x5 0,25 c) (1,0 điểm) 2( 2  1) 2( 2  1) A= . 0,5 2 1 2 1 = 2. 2  2 0,5 2 a) (1,0 điểm) (1,0 điểm) Vì đồ thị hàm số (1) đi qua A(1; 4) nên 4  m  1  m  3 0,5 Vậy m  3 đồ thị hàm số (1) đi qua A(1; 4) . Vì m  3  0 nên hàm số (1) đồng biến trên  . 0,5 b) (1,0 điểm) m 2  m Đồ thị hàm số (1) song song với d khi và chỉ khi  m  1  1 0,5  m  1. Vậy m  1 thỏa mãn điều kiện bài toán. 0,5 3 (1,5 điểm) Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x km/h, x  0 . 36 0,25 Thời gian của người đi xe đạp khi đi từ A đến B là x Vận tốc của người đi xe đạp khi đi từ B đến A là x+3 36 0,25 Thời gian của người đi xe đạp khi đi từ B đến A là x3 36 36 36 Ta có phương trình:   0,25 x x  3 60  x  12 Giải phương trình này ra hai nghiệm  0,5  x  15  loai   Vậy vận tốc của người đi xe đạp khi đi từ A đến B là 12 km/h 0,25
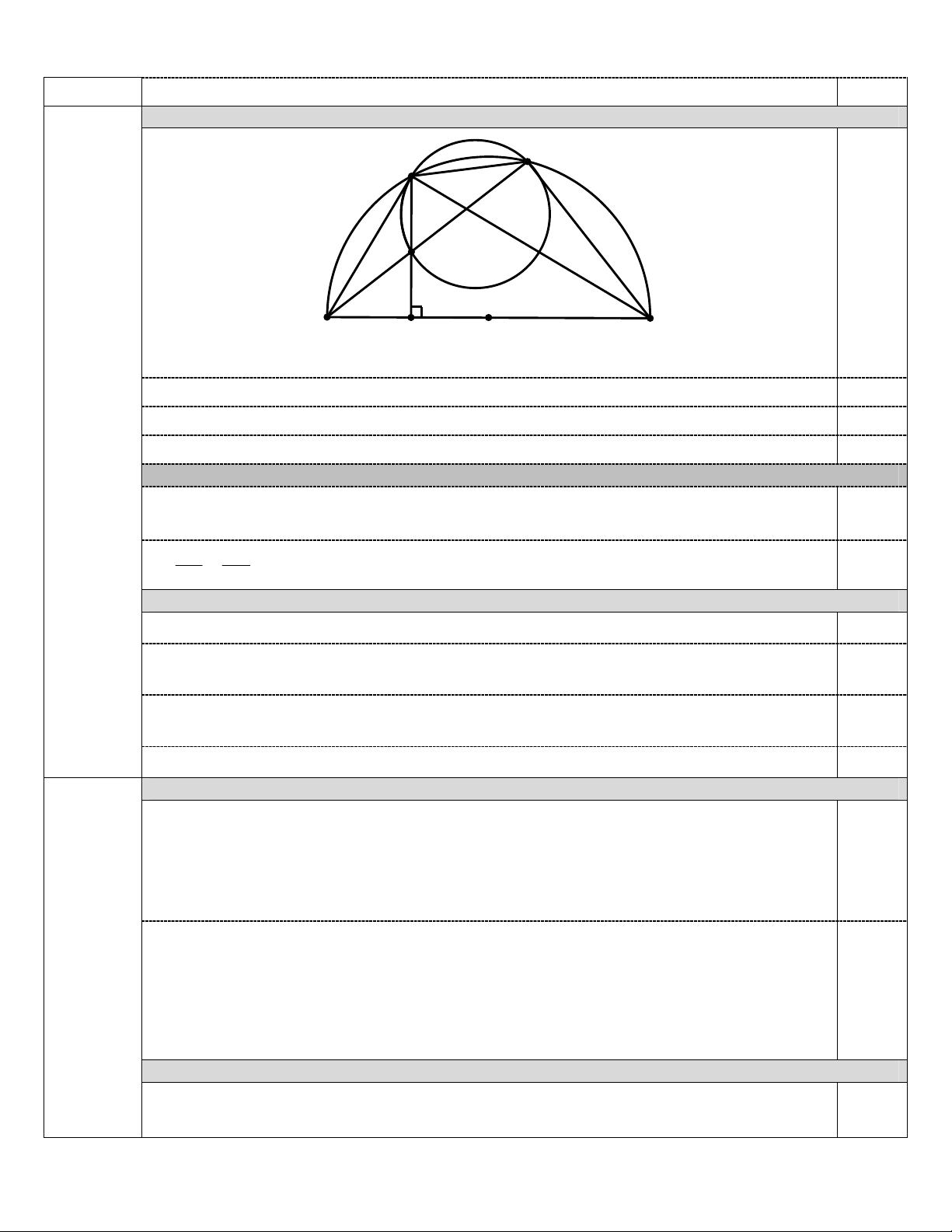
www.VNMATH.com 4 a) (1,0 điểm) (3,0 điểm) D A I 0,25 B H O C Vẽ hình đúng, đủ phần a.  AH  BC  IHC  900. (1) 0,25  0  BDC  90 ( góc nội tiếp chắn nửa đường tròn) hay IDC  90 . (2) 0 0,25   Từ (1) và (2)  IHC  IDC  1800  IHCD là tứ giác nội tiếp. 0,25 b) (1,0 điểm) Xét ABI và DBA có góc B chung, BAI   (Vì cùng bằng  ).   ADB ACB 0,75 Suy ra, hai tam giác ABI , DBA đồng dạng. AB BD    AB 2  BI .BD . (đpcm) 0,25 BI BA c) (1,0 điểm) BAI   (chứng minh trên).  ADI 0,25  AB là tiếp tuyến của đường tròn ngoại tiếp  ADI với mọi D thuộc cung AD và A là 0,25 tiếp điểm. (tính chất góc tạo bởi tiếp tuyến và dây cung) Có AB  AC tại A  AC luôn đi qua tâm đường tròn ngoại tiếp AID . Gọi M là tâm 0,25 đường trong ngoại tiếp AID  M luôn nằm trên AC. Mà AC cố định  M thuộc đường thẳng cố định. (đpcm) 0,25 5 a) (1,0 điểm) (1,5 điểm) x 2  2 y 2  3 xy  2 x  4 y  3  0   x  y  x  2 y   2  x  2 y   3   x  2 y  x  y  2   3 0,5 Do x, y nguyên nên x  2 y , x  y  2 nguyên Mà 3   1 .3   3 .1 nên ta có bốn trường hợp  x  2 y  1 x  3 x  2 y  3  x  9   ;   loai   x  y  2  3  y  2  x  y  2  1  y  6  x  2 y  1  x  11  x  2 y  3 x  1 0,5    loai  ;    x  y  2  3  y  6  x  y  2  1  y  2 Vậy các giá trị cần tìm là ( x; y )  (1; 2), (3; 2) . b) (0,5 điểm) Vẽ đường tròn đường kính BD. Do các góc A, C tù nên hai điểm A, C nằm trong đường tròn đường kính BD. Suy ra, AC  BD (Do BD là đường kính). 0,5
www.VNMATH.com Lưu ý: - Thí sinh làm theo cách riêng nhưng đáp ứng được yêu cầu cơ bản vẫn cho đủ điểm. - Việc chi tiết hoá điểm số (nếu có) so với biểu điểm phải đảm bảo không sai lệch với hướng dẫn chấm và được thống nhất trong hội đồng chấm. - Điểm toàn bài không làm tròn số ( ví dụ: 0,25, hoặc 0,75 vẫn giữ nguyên ).
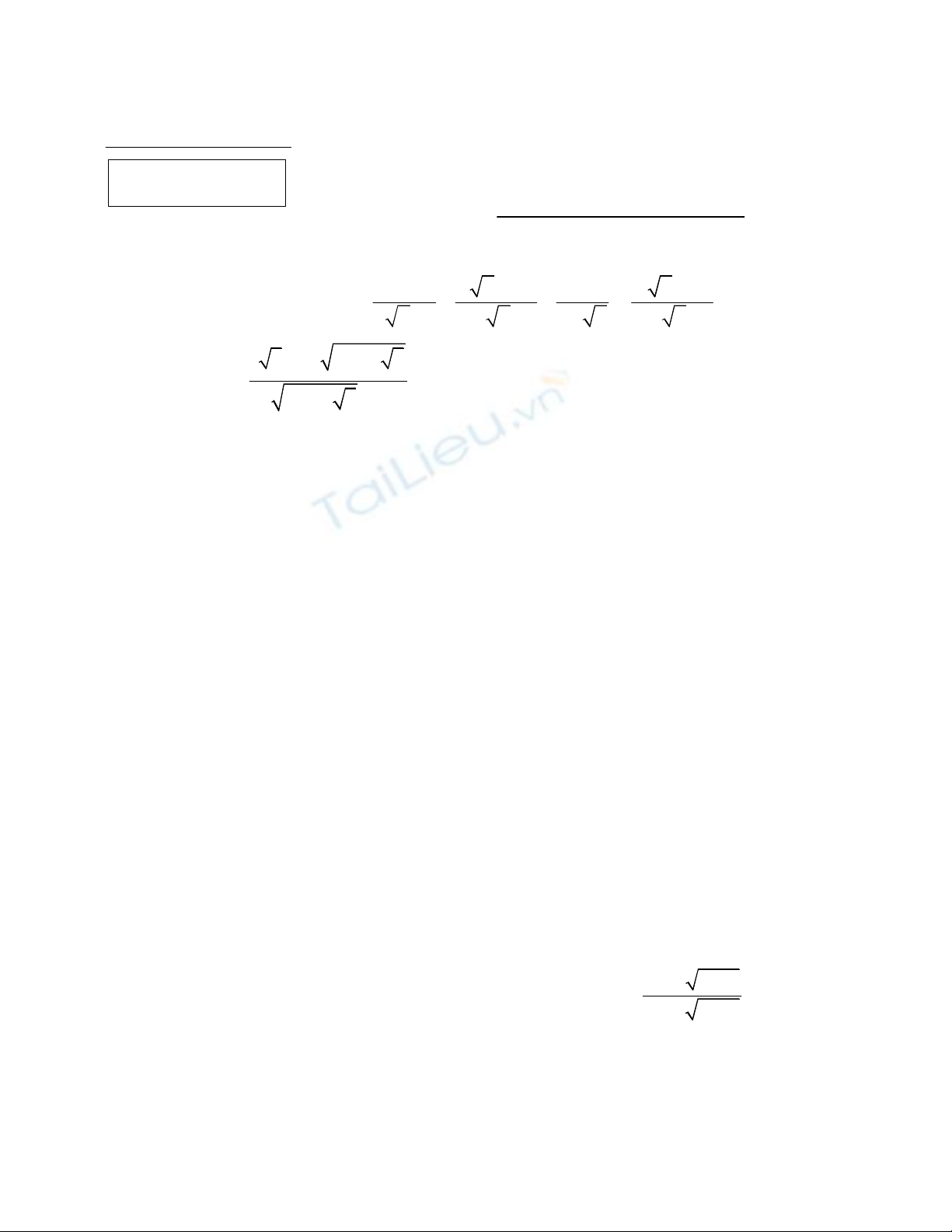
www.VNMATH.com UBND TỈNH BẮC NINH ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2013 – 2014 Môn thi: Toán (Dành cho thí sinh thi vào chuyên Toán, Tin) ĐỀ CHÍNH THỨC Thời gian làm bài: 150 phút (Không kể thời gian giao đề) Ngày thi: 20 tháng 6 năm 2013 Câu 1. (1,5 điểm)  x2 x2 1  x 1 a) Rút gọn biểu thức A     : với x  0, x  1 .  x x 1 x  x 1 1  x  x  x 1 b) Cho x    3  1 . 3 10  6 3 2013 , tính giá trị của biểu thức P   x 2  4 x  2  . 21  4 5  3 Câu 2. (2,0 điểm) Cho phương trình: 2 x2  4mx  2m2  1  0 (1), với x là ẩn, m là tham số. a) Chứng minh với mọi giá trị của m, phương trình (1) luôn có hai nghiệm phân biệt. b) Gọi hai nghiệm của phương trình (1) là x1 , x2 . Tìm m để 2 x12  4mx2  2m2  9  0. Câu 3. (1,5 điểm) a) Cho các số dương x, y thỏa mãn x  y  x 3  y 3 . Chứng minh rằng x 2  y 2  1. 2 x  y 2  1  b) Giải hệ phương trình: 2 y  z 2  1. 2 z  x 2  1  Câu 4. (3,0 điểm) Cho đường tròn tâm O đường kính BC  2 R , điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ hai tiếp tuyến AM, AN với đường tròn (O) (M, N là hai tiếp điểm). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng: a) Năm điểm A, O, M, N, F cùng nằm trên một đường tròn; b) Ba điểm M, N, H thẳng hàng; c) HA.HF  R 2  OH 2 . Câu 5. (2,0 điểm) x  y 2013 a) Tìm tất cả các bộ số nguyên dương  x; y; z  thỏa mãn là số hữu tỷ, y  z 2013 đồng thời x 2  y 2  z 2 là số nguyên tố. b) Tính diện tích của ngũ giác lồi ABCDE, biết các tam giác ABC, BCD, CDE, DEA, EAB cùng có diện tích bằng 1. ------------Hết------------
www.VNMATH.com UBND TỈNH BẮC NINH HƯỚNG DẪN CHẤM SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN NĂM HỌC 2013 – 2014 Môn thi: Toán (Dành cho thí sinh thi vào chuyên Toán, Tin) Câu Lời giải sơ lược Điểm 1 a) (1,0 điểm) (1,5 điểm) x  2  x  x  2  x  x 1 x  x 1 A  0,5 ( x  1)( x  x  1) x 1 x 1 x  x 1    1. 0,5 ( x  1)( x  x  1) x 1 b) (0,5 điểm) x   3  1 . 3 ( 3  1)3  ( 3  1)( 3  1)  2  5  2. 0,25 ( 20  1) 2  3 20  4 2( 5  2)  x 2  4 x  1  0  P  1 0,25 2 a) (1,0 điểm) (2,0 điểm)  '  4m 2  2(2m 2  1)  2  0 với mọi m. 0,5 Vậy (1) luôn có hai nghiệm phân biệt với mọi m. 0,5 b) (1,0 điểm) Theo ĐL Viét ta có x1  x2  2m . Do đó, 2 x12  4mx2  2m 2  9  (2 x12  4mx1  2m2  1)  4m( x1  x2 )  8. 0,5  8m 2  8  8(m  1)(m  1) (do 2 x12  4mx1  2m 2  1  0 ). Yêu cầu bài toán: (m  1)(m  1)  0  1  m  1 . 0,5 3 a) (0,5 điểm) (1,5 điểm) Do x 3  0, y 3  0 nên x  y  0 . 0,5 x  y  x 3  y 3  x 3  y 3  1  x 2  xy  y 2  x 2  y 2  1. b) (1,0 điểm) Cộng vế với vế các phương trình của hệ ta được: 2 2 2 0,5 x 2  2 x  1  y 2  2 y  1  z 2  2 z  1  0   x  1   y  1   z  1  0 (1). 2 2 2 Do  x  1  0,  y  1  0,  z  1  0 nên VT 1  VP 1 . 0,5 Dấu bằng xảy ra khi và chỉ khi x  y  z  1 .
www.VNMATH.com Thử lại, x  y  z  1 là nghiệm của hệ. 4 a) (1,0 điểm) (3,0 điểm) A D N H M I 0,25 B C F O Vẽ hình câu a) đúng, đủ. Do các điểm M, N, F cùng nhìn đoạn AO dưới góc 900 nên A, O, M, N, F cùng thuộc đường tròn đường kính AO. 0,75 b) (1,0 điểm) Ta có AM  AN (Tính chất tiếp tuyến). 0,25 Từ câu a) suy ra    (1). ANM AFN Mặt khác, vì hai tam giác ADH, AFC đồng dạng; hai tam giác ADN, ANC đồng dạng nên AH AN 0,25 AH . AF  AD. AC  AN 2   . AN AF Do đó, hai tam giác ANH, AFN đồng dạng (c.g.c)     (2). ANH AFN 0,25 Từ (1), (2) ta có      H  MN  đpcm. ANH ANM 0,25 c) (1,0 điểm) Từ câu a) ta có HM .HN  HA.HF . 0,25 Gọi I  OA  MN ta có I là trung điểm của MN. HM .HN   IM  IH  IM  IH   IM 2  IH 2 0,25    OM 2  OI 2  OH 2  OI 2  R 2  OH 2 0,25 Từ đó suy ra HA.HF  R 2  OH 2 . 0,25 5 a) (1,0 điểm) (2,0 điểm) x  y 2013 m Ta có   m, n  * ,  m, n   1 . y  z 2013 n 0,25 nx  my  0 x y m  nx  my  mz  ny  2013       xz  y 2 . mz  ny  0 y z n 2 2 x 2  y 2  z 2   x  z   2 xz  y 2   x  z   y 2   x  y  z  x  z  y  . 0,25
www.VNMATH.com 2 2 2 x2  y2  z2  x  y  z Vì x  y  z  1 và x  y  z là số nguyên tố nên  0,25 x  y  z  1 Từ đó suy ra x  y  z  1 (thỏa mãn). 0,25 b) (1,0 điểm) A B E C I 0,25 D Gọi I  EC  BD Ta có S BAE  S DAE nên khoảng cách từ B, D đến AE bằng nhau. Do B, D cùng phía đối với đường thẳng AE nên BD / / AE . Tương tự AB / / CE Do đó, ABIE là hình bình hành  S IBE  S ABE  1 0,25 Đặt S ICD  x  0  x  1  S IBC  S BCD  S ICD  1  x  S ECD  S ICD  S IED  3 5 S IC S IBC x 1 x x   x 2  3x  1  0   2 Lại có ICD   hay  S IDE IE S IBE 1 x 1  3 5 0,25 x   2 3 5 5 1 Kết hợp điều kiện ta có x   S IED  2 2 5 1 5  5 Do đó S ABCDE  S EAB  S EBI  S BCD  S IED  3   . 0,25 2 2 Lưu ý: - Thí sinh làm theo cách riêng nhưng đáp ứng được yêu cầu cơ bản vẫn cho đủ điểm. - Việc chi tiết hóa điểm số (nếu có) so với biểu điểm phải đảm bảo không sai lệch với hướng dẫn chấm và được thống nhất trong hội đồng chấm. - Điểm toàn bài không làm tròn số ( ví dụ: 0,25, hoặc 0,75 vẫn giữ nguyên ).

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.