Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
303
ỨNG DỤNG THUẬT TOÁN TỐI ƯU METAHEURISTIC
TRONG VẬN HÀNH KINH TẾ CÁC TỔ MÁY NHIỆT ĐIỆN
Nguyễn Công Chính, Trần Văn Đại
Trường Đại học Thủy lợi, email: chinhnc@tlu.edu.vn
1. GIỚI THIỆU
Bài toán vận hành kinh tế các tổ máy nhiệt
điện là một trong những vấn đề cơ bản trong
vận hành hệ thống điện. Về bản chất, đây là
bài toán tối ưu hóa và mục tiêu của nó là
giảm tổng chi phí phát điện của các tổ máy,
đồng thời đáp ứng các ràng buộc. Tuy nhiên,
hàm mục tiêu và các ràng buộc của bài toán
vận hành kinh tế các tổ máy nhiệt điện
thường không phải là tuyến tính [1]. Do đó,
việc sử dụng các phương pháp truyền thống
là chưa thực sự hiệu quả. Tại Việt nam, một
số tác giả cũng đã nghiên cứu giải bài toán về
phối hợp các tổ máy phát nhiệt điện [2]; Tuy
nhiên, thuật toán tối ưu metaheuristic chưa
được đề cập đến.
Bài báo này tập trung vào việc áp dụng
thuật toán Particle Swarm Optimization (PSO)
[3] để giải quyết bài toán vận hành kinh tế các
tổ máy nhiệt điện. Kết quả được so sánh với
phương pháp lặp Lambda truyền thống.
2. VẬN HÀNH KINH TẾ CÁC TỔ MÁY
NHIỆT ĐIỆN
Mục tiêu chính của bài toán vận hành kinh
tế các tổ máy nhiệt điện là giảm thiểu tổng
chi phí nhiên liệu trong khi vẫn đáp ứng được
ràng buộc vận hành trong hệ thống điện.
Trong đó, việc phân bổ sản lượng điện tối
ưu giữa các tổ máy phát điện khác nhau với
chi phí tối thiểu có thể được thực hiện theo
cách đáp ứng được ràng buộc về nhu cầu tải
và giới hạn về phát điện.
2.1. Hàm mục tiêu
Bài toán có thể được xây dựng bằng hàm
bậc hai theo phương trình sau [1]:
0
g
N
g
iigi
i
FP FP
(1)
trong đó:
F(Pgi): Tổng chi phí nhiên liệu;
Fi(Pgi): Chi phí nhiên liệu của tổ máy phát
thứ i;
Ng: Số lượng tổ máy.
Chi phí nhiên liệu của tổ máy phát thứ i có
thể được biểu diễn như sau:
2
igi igi igi i
FP aP bP c

(2)
trong đó:
ai, bi, ci: Hệ số chi phí nhiên liệu của tổ
máy phát thứ i.
2.2. Ràng buộc bình đẳng
Thông thường, trong một hệ thống điện,
lượng điện năng được tạo ra phải đủ để đáp
ứng nhu cầu phụ tải cộng với tổn thất trên
đường dây truyền tải. Do các đường dây
truyền tải được đặt giữa các tổ máy phát điện
và phụ tải, nên tổn thất có thể xảy ra ở bất kỳ
đâu trước khi công suất được truyền đến tải:
1
g
N
g
i Load Loss
iPP P

(3)
trong đó:
Pgi: Công suất thực của máy phát điện thứ i;
PLoad: Tổng nhu cầu điện năng thực tế;
PLoss: Tổn thất truyền tải điện.
Ma trận B hay còn gọi là ma trận hệ số tổn
thất truyền tải là ma trận vuông có kích thước
Ng×Ng trong đó Ng là số đơn vị phát điện
trong hệ thống. Phương trình (4) trình bày
cách tính Ploss là tổn thất truyền tải qua ma
trận B [1].
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
304
ij
11
gg
NN
L
oss gi gj
ij
P
PBP

 (4)
trong đó:
Pgi, Pgj: Sản lượng điện thực tế lần lượt ở
nút thứ i và thứ j;
Bij = Bji: Hệ số tổn thất.
2.3. Ràng buộc bất bình đẳng
Ràng buộc bất bình đẳng thường liên quan
đến giới hạn về công suất phát điện của từng
tổ máy. Cụ thể, công suất phát điện của mỗi
tổ máy phải tuân theo các ràng buộc bất bình
đẳng sau:
min max
g
igigi
PPP (5)
trong đó:
min
i
P: Giới hạn phát điện tối thiểu của tổ
máy phát điện thứ i;
max
g
i
P: Giới hạn phát điện tối đa của tổ máy
phát điện thứ i.
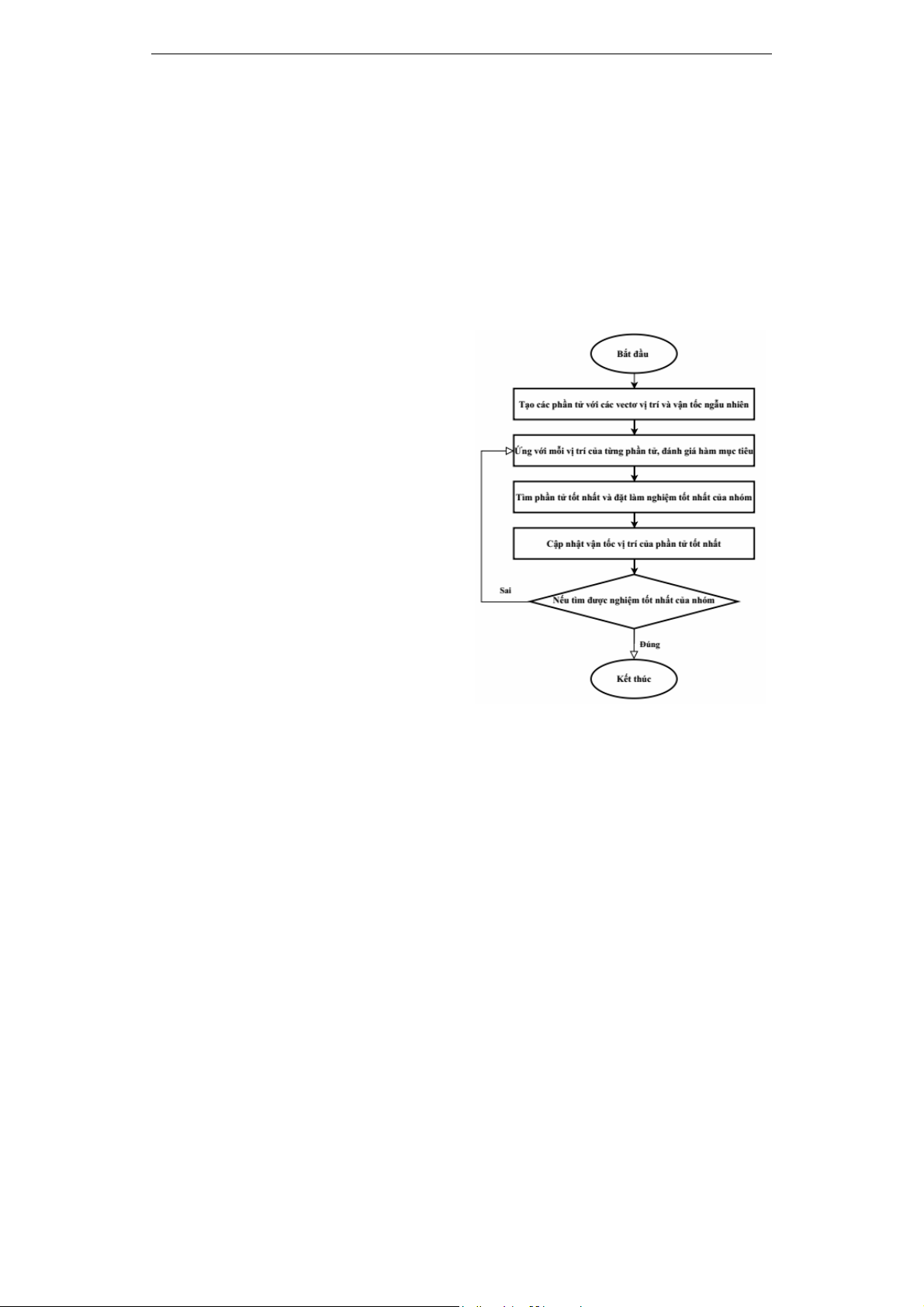
3. THUẬT TOÁN TỐI ƯU HÓA PSO
Thuật toán tối ưu hóa PSO được đề xuất
bởi Kennedy và Eberhart vào năm 1995. PSO
là một thuật toán tối ưu hóa được lấy cảm
hứng từ hành vi tập thể của các sinh vật tự
nhiên như đàn cá hay đàn chim. Trong PSO,
một nhóm các phần tử (đại diện cho các
nghiệm tiềm năng) di chuyển trong không
gian nghiệm của bài toán để tìm ra nghiệm
tốt nhất. Mỗi phần tử điều chỉnh vị trí của
mình dựa trên nghiệm tốt nhất mà nó biết
(pbest) và nghiệm tốt nhất mà toàn bộ nhóm
phát hiện ra (gbest). Sự di chuyển hợp tác
này cho phép các phần tử hội tụ về phía các
nghiệm tối ưu qua các lần lặp. Mỗi phần tử
trong nhóm được đặc trưng bởi vị trí và vận
tốc của nó trong không gian nghiệm. Vị trí
của mỗi phần tử được cập nhật theo công
thức sau:
11ttt
iii
x
xv

 (6)
trong đó:
t
i
x
là vị trí của phần tử i tại thời điểm t;
1t
i
v là vận tốc của phần tử i tại thời điểm
t+1.
Vận tốc của mỗi phần tử được cập nhật
theo công thức sau:

1
11 2 2
w
tt t t
ii ii ii
v v c r pbest x c r gbest x

(7)
trong đó:
w là hệ số giảm tốc;
c1 và c2 là hằng số tăng tốc;
r1, r2 là số ngẫu nhiên nằm trong khoảng
[0,1];
pbesti là nghiệm tốt nhất mà phần tử i đã
tìm thấy, gbesti là nghiệm tốt nhất mà toàn bộ
nhóm đã tìm thấy. Các bước thuật toán liên
quan đến kỹ thuật tối ưu hóa được thể hiện
trong hình 1:
Hình 1. Sơ đồ thuật toán PSO
4. KẾT QUẢ TÍNH TOÁN
Một hệ thống gồm 3 tổ máy nhiệt điện với
giới hạn công suất và hàm chi phí nhiên liệu
của từng tổ máy thể hiện trong bảng 1 được
sử dụng để đánh giá sự hiệu quả của thuật
toán PSO. Kết quả thu được từ PSO được so
sánh với phương pháp lặp Lambda. Ma trận
tổn thất B sử dụng để tính toán tổn thất
truyền tải được thể hiện bằng phương trình
(8). Trong nghiên cứu này, phần mềm
MATLAB được sử dụng để tính toán và mô
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
305
phỏng. Với giả thiết nhu cầu của phụ tải là
300 MW, kết quả tính toán thể hiện trong
bảng 2 cho thấy phương pháp được đề xuất
(PSO) có kết quả tốt hơn so với phương pháp
truyền thống (Lambda).
Bảng 1. Công suất và hệ số tổ máy phát điện
Pgi
min
g
i
P
(MW)
max
g
i
P
(MW) ai bi ci
1 100 400 0,004 8 180
2 50 350 0,0048 6,4 240
3 50 300 0,0035 7 120
ij
0,00841 0,00002 0,00038
0,00002 0,00598 0,00019
0,00038 0,00019 0,00009
B






(8)
Bảng 2. Công suất đầu ra tối ưu
cho hệ thống 3 tổ máy
Tải
(MW) PP P1
(MW)
P2
(MW)
P3
(MW)
T. Thất
(MW)
Lambda 191,5378 70,68289 50 12,22
300 PSO 190,2355 70,68517 50 10,92
5. KẾT LUẬN
Từ kết quả nghiên cứu cho thấy việc áp
dụng thuật toán tối ưu metaheuristic để giải
bài toán vận hành kinh tế các tổ máy nhiệt
điện là hoàn toàn phù hợp và hiệu quả. Trong
các nghiên cứu tiếp theo, tác giả sẽ tập trung
nghiên cứu một số các thuật toán
metaheuristic khác để giải quyết bài toán vận
hành kinh tế các tổ máy nhiệt điện cũng như
các bài toán vận hành hệ thống điện khác.
6. TÀI LIỆU THAM KHẢO
[1] J. Grainger, W. Stevenson, and G. W.
Chang, Power System Analysis (SI), 2nd
Edition, McGraw Hill International, 2021.
[2] Trung, Đào Minh, "Phối hợp các tổ máy
phát nhiệt điện", Tạp chí Khoa học Đại học
Cần Thơ 26 (2013): 44-52.
[3] J. Kennedy and R. Eberhart. "Particle
Swarm Optimization", Proceedings of
ICNN'95 - International Conference on
Neural Networks. Vol. 4. IEEE, 1995.