29
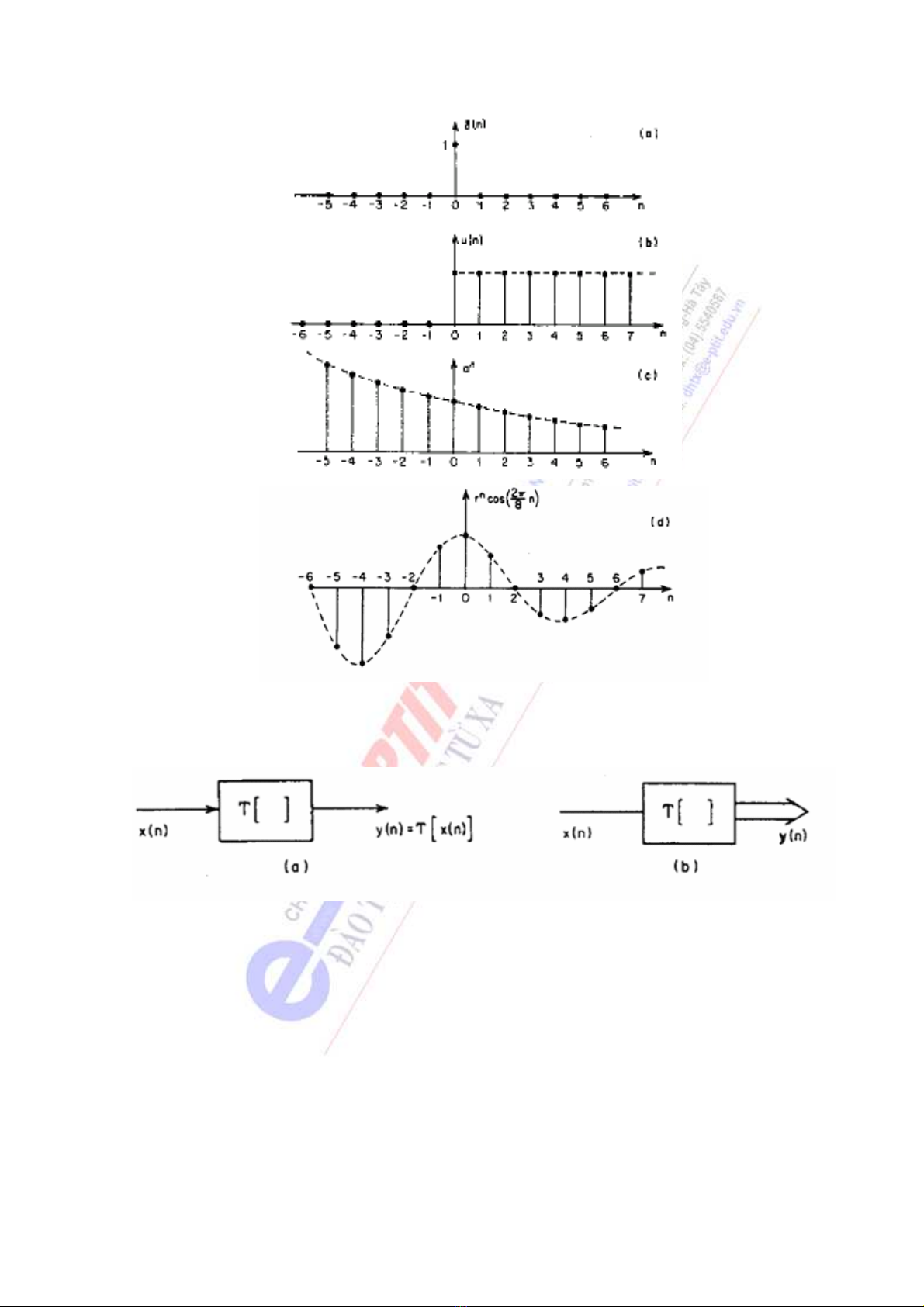
Hình 1.30 (a) Lấy mẫu đơn vị, (b) đơn vị bước, (c) hàm mũ thực và (d) hàm sin suy giảm
Hình 1.31 Sơ đồ khối (a) hệ thống đơn ngõ vào/đơn ngõ ra; (b) hệ thống đơn ngõ vào/đa ngõ ra
Khi hệ thống gồm nhiều ngõ ra, tín hiệu chuỗi ngõ ra sẽ được biểu diễn bằng một vector
được mô tả như ở Hình 1.31.
Hệ thống tuyến tính dịch bất biến là hệ thống đặc biệt hữu dụng cho việc xử lý tín hiệu âm
thoại. Hệ thống được đặc trưng bởi đáp ứng xung, )(nh , khi đó tín hiệu ngõ ra được tính bởi
công thức
∑
∞
−∞=
=−=
k
nhnxknhkxny )(*)()()()( (1.52a)
30
∑
∞
−∞=
=−=
k
nxnhknxkhny )(*)()()()( (1.52b)
với * là phép chập hai tín hiệu
1.3 LÝ THUYẾT VÀ CÁC BÀI TOÁN CƠ BẢN
1.3.1 Phân tích dự đoán tuyến tính [12]
Dự đoán tuyến tính (Linear prediction, viết tắt là LP) là một phần không thể thiếu của hầu
hết tất cả giải thuật mã hóa thoại hiện đại ngày nay. Ý tưởng cơ bản là một mẫu thoại có thể được
xấp xỉ bằng một kết hợp tuyến tính của các mẫu trong quá khứ. Trong một khung tín hiệu, các
trọng số dùng để tính toán kết hợp tuyến tính được tìm bằng cách tối thiểu hóa bình phương trung
bình lỗi dự đoán; các trọng số tổng hợp, hoặc các hệ số dự đoán tuyến tính (LPC) được dùng đại
diện cho một khung cụ thể.
Trong phần chương 3, sự sắp xếp LP theo hệ thống dựa trên mô hình ngược tự động
Trong thực tế, phân tích dự là một tiến trình ước lượng để tìm các thông số của AR, mà
các thông số này được cho bởi các mẫu của tín hiệu. Như vậy, LP là một kỹ thuật nhận dạng với
các thông số của một hệ thống đựoc tìm từ việc quan sát. Với giả định là tín hiệu thoại được mô
hình như là tín hiệu AR, điều này đã được chứng minh tính đúng đắn của nó trong thực tiễn.
Một cách biểu diễn LP khác là phương pháp ước lượng phổ. Như đã trình bày ở trên, phân
tích LP cho phép việc tính toán các thông số của AR, đã được định nghĩa trong mật độ phổ công
suất (PSD) của chính bản thân tín hiệu. Bằng cách tính toán LPC của một khung tín hiệu, ta có thể
tạo ra một tín hiệu khác theo cách thức có nội dung phổ gần như tương đồng với tín hiệu gốc.
LP cũng có thể được xem như là một quá trình loại bỏ các dư thừa khi thông tin bị lặp lại
trong một sự trường hợp cần khử. Sau cùng, việc truyền dữ liệu có thể không cần thiết nếu như dữ
liệu cần truyền có thể được dự đoán trước. Bằng cách thức chuyển chỗ các dư thừa trong một tín
hiệu, số lượng bit cần thiết để mang thông tin sẽ ít hơn và như thế sẽ đạt được mục tiêu nén dữ
liệu.
Trong phần này sẽ đề cập đến bài toán cơ bản của phân tích LP đã được định rõ, kết hợp
với việc hiệu chỉnh lại cho phù hợp theo hướng các tín hiệu động, cũng như ví dụ và các giải thuật
cần thiết cho quá trình dự đoán tuyến tính.
1.3.1.1 Bài toán dự đoán tuyến tính
Dự đoán tuyến tính được mô tả như là một bài toán nhận dạng hệ thống, với các thông số
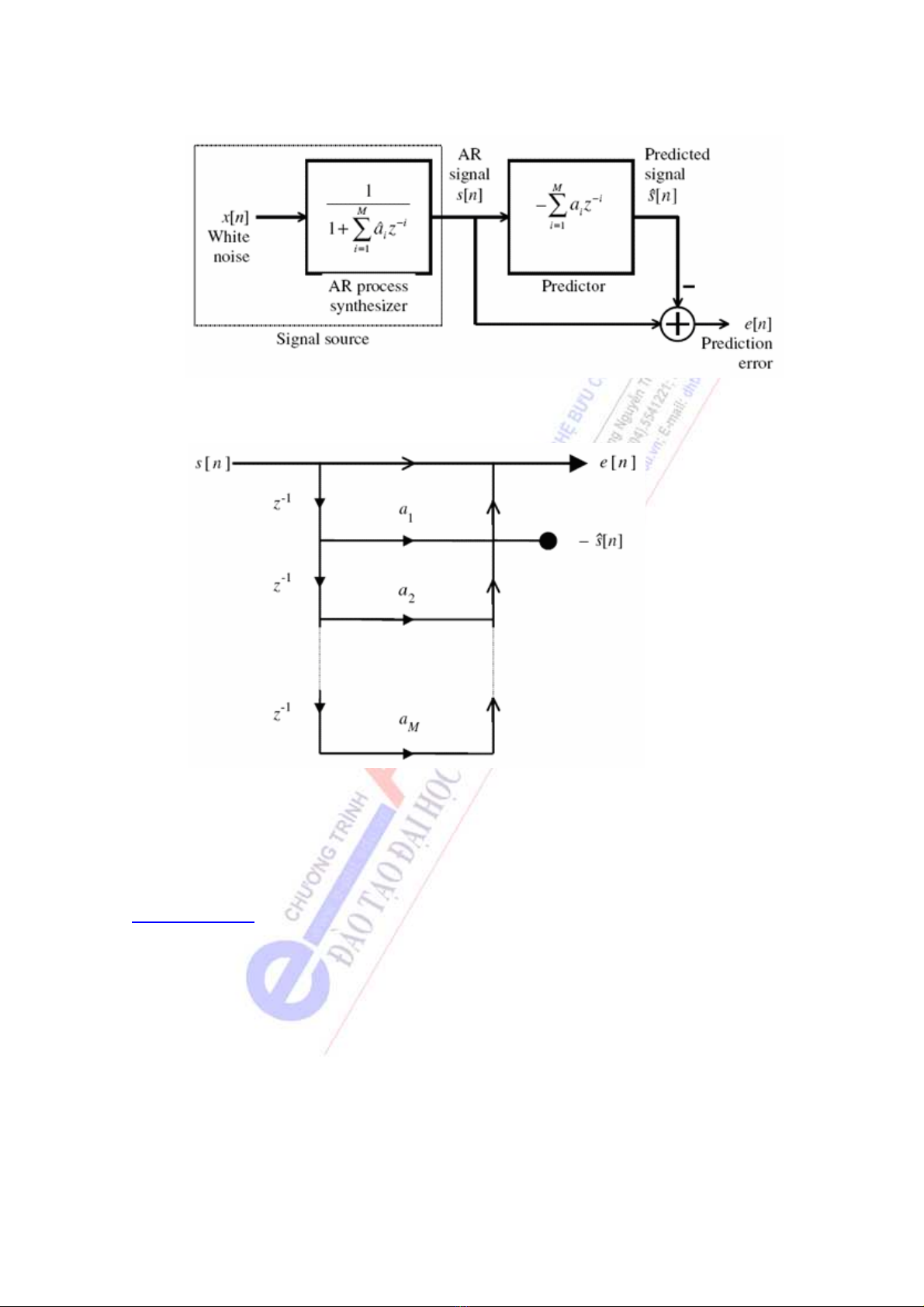
của một mô hình AR được ước lượng từ bản thân tín hiệu. Mô hình được trình bày ở Hình 1.32.
Tín hiệu nhiễu trắng ][n
x
được lọc bởi quá trình tổng hợp AR để có được tín hiệu AR ][n
s
, với
các thông số AR được ký hiệu là i
a
^
. Dự đoán tuyến tính thực hiện ước đoán ][n
s
dựa vào
M
mẫu trong quá khứ:
][][
1
^
insan
M
i
i
s−−= ∑
=
(1.53)
Với i
alà các ước lượng của các thông số AR được xem là các hệ số dự đoán tuyến tính
(LPC). Hằng số
M
trong công thức là bậc dự đoán. Như vậy, việc dự đoán dự trên tổ hợp tuyến
tính của
M
mẫu trong quá khứ của tín hiệu, chính vì thế việc dự đoán mang tính tuyến tính. Lỗi
dự đoán được tính bằng công thức:
31
][][][ ^
nsnsne −= (1.54)
Hình 1.32 Hệ thống nhận dạng dưới dạng dự đoán tuyến tính
Hình 1.33 Bộ lọc lỗi dự đoán
Lỗi dự đoán chính là độ sai biệt giữa mẫu thật sự và mẫu ước lượng. Hình 1.33 mô tả lưu
đồ tín hiệu thực hiện bộ lọc lỗi dự đoán. Bộ lọc có ngõ vào là tín hiệu AR và ngõ ra chính là tín
hiệu lỗi dự đoán.
Tối thiểu hoá lỗi
Bài toán nhận dạng hệ thống bao gồm việc ước lượng các thông số AR i
a
^
từ ][n
s
. Để
thực hiện việc ước lượng, tiêu chuẩn phải được thiết lập. Trong đó, bình phương trung bình lỗi dự
đoán được tính bởi công thức:
{}
⎭
⎬
⎫
⎩
⎨
⎧⎟
⎠
⎞
⎜
⎝
⎛−+== ∑
=
2
1
2][][][ M
i
iinsansEneEJ (1.55)
Được tối thiểu hóa bằng cách lựa chọn LPC thích hợp. Thông số LPC tối ưu có thể được
tìm bằng cách thiết lập các đạo hàm riêng phần của
J
khi i
atiến tới zero:
32
0][][][2
1
=
⎭
⎬
⎫
⎩
⎨
⎧−
⎟
⎠
⎞
⎜
⎝
⎛−+=
∂
∂∑
=
knsinsansE
a
JM
i
i
k
(1.56)
Với Mk ,...,2,1=, khi (4.4) xảy ra thì i
iaa
^
=, lúc này LPC chính bằng các thông số
AR.
Độ lợi dự đoán
Độ lợi dự đoán của bộ dự đoán được cho bởi công thức
{
}
{}
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=][
][
log10log10 2
2
10
2
2
10 neE
nsE
PG
e
s
σ
σ
(1.57)
Là tỉ số giữa biến tín hiệu ngõ vào và biến của lỗi dự đoán theo đơn vị decibels (dB). Độ
lợi dự đoán là thông số đo lường chất lượng của bộ dự đoán. Một bộ dự đoán tốt hơn có khả năng
tạo ra lỗi dự đoán nhỏ hơn với độ lợi cao hơn.
Tối thiểu hóa bình phương trung bình lỗi dự đoán
Từ Hình 1.33, ta có thể nhận xét khi i
iaa
^
=, thì ][][ n
x
ne
=
; như vậy lỗi dự đoán tương
tự như dùng tín hiệu nhiễu trắng để tạo ra tín hiệu AR ][n
s
. Đây là trường hợp tối ưu khi lỗi bình
phương trung bình được tối thiểu hóa, với
}
{
}
222
min ][][ x
nxEneEJ
σ
=== (1.58)
Khi đó, độ lợi dự đoán đạt giá trị lớn nhất.
Điều kiện tối ưu có thể đạt được khi bậc của bộ dự đoán lớn hơn hoặc bằng bậc của quá
trình tổng hợp AR. Trong thực tế,
M
thường là số chưa biết trước. Một phương pháp đơn giản để
có thể ước lượng được giá trị
M
từ tín hiệu nguồn là vẽ biểu đồ độ lợi dự đoán như là một hàm
của bậc dự đoán. Với phương pháp này, ta có thể quyết định được bậc của dự đoán ứng với độ lợi
bão hòa, khi đó khi tăng bậc dự đoán thì độ lợi không tăng. Giá trị của bậc dự đoán tại điểm thỏa
điều kiện bão hòa này được xem là giá trị ước lượng tốt nhất cho bậc của tín hiệu AR.
Sau khi đã xác định được giá trị M, hàm chi phí
J
đạt giá trị tối thiểu khi i
iaa
^
=, dẫn đến
][][ n
x
ne =. Và khi đó, lỗi dự đoán sẽ bằng với giá trị tín hiệu đầu vào của bộ tổng hợp quá trình
AR.
1.3.1.2 Phân tích dự đoán tuyến tính cho tín hiệu động
Tín hiệu thoại trong thực tế là tín hiệu động, nên LPC phải được tính ứng với từng khung
tín hiệu. Trong một khung tín hiệu, một tập LPC được tính toán và dùng để đại diện cho các thuộc
tính của tín hiệu trong một chu kỳ cụ thể, với giả định rằng số liệu thống kê của tín hiệu vẫn
không thay đổi trong một khung. Quá trình tính toán LPC từ dữ liệu tín hiệu được gọi là phân tích
dự đoán tuyến tính.
Bài toán dự đoán tuyến tính cho tín hiệu động được phát biểu lại như sau: đây là bài toán
thực hiện việc tính các giá trị LPC ứng với
N
điểm dữ liệu với thời gian kết thúc là m:
]1[ +−
N
m
s
, ]2[ +−
N
m
s
, …, ][m
s
. Vector LPC được viết như sau:
[] []
[
]
[
][]
T
Mmamamama ...
21
= (1.59)
33
Với
M
là bậc dự đoán
Độ lợi dự đoán
Độ lợi dự đoán của bộ dự đoán được cho bởi công thức
[] []
[]
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=∑
∑
+−=
+−=
m
Nmn
m
Nmn
ne
ns
mPG
1
2
1
2
10
log10 (1.60)
Với
[] [] [] [] [ ][ ]
insmansnsnsne
M
i
i−+=−= ∑
=1
^
; 1+
−
=
N
mn , …, m (1.61)
Các LPC
[
]
mai được tính toán từ các mẫu trong chu kỳ. Độ lợi dự đoán định nghĩa ở
công thức (4.23) là một hàm theo biến thời gian m.
Ví dụ: Nhiễu trắng được tạo ra bởi bộ tạo số ngẫu nhiên phân phối đều, sau đó được lọc
bởi bộ tổng hợp AR với
534.1
1=a 1
2=a 587.0
3
=
a 347.0
4
=
a 08.0
56 =a
061.0
6−=a 172.0
7−=a 156.0
8
−
=
a 157.0
9
−
=
a 141.0
10 −=a
Khung tổng hợp của tín hiệu AR được dùng cho phân tích LP, với tổng cộng là 240 mẫu.
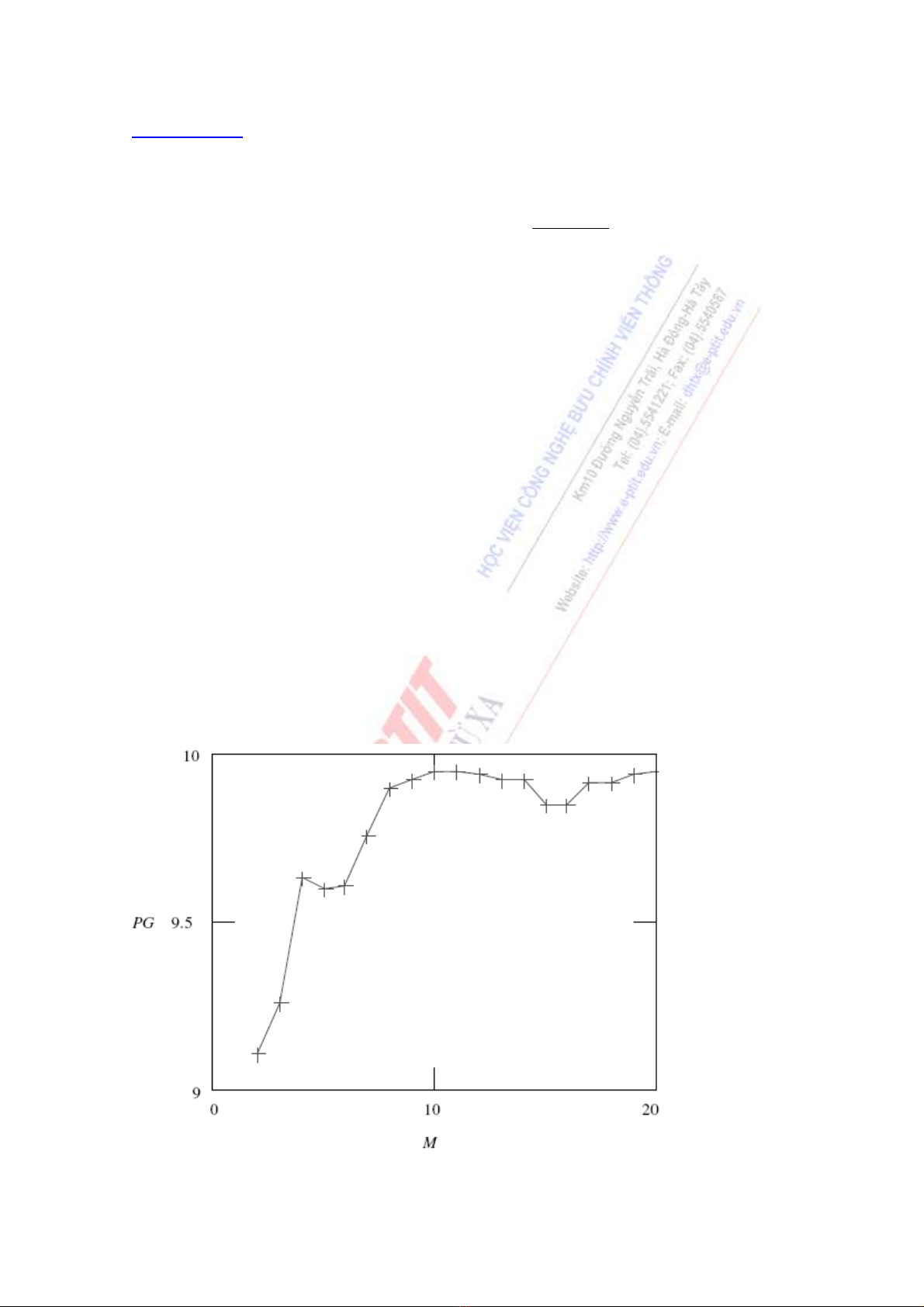
Ước lượng tự động tương quan không hồi qui sử dụng cửa sổ Hamming. Phân tích LP được thực
hiện với bậc từ 2 đến 20. Hình 1.34 tóm tắt kết quả, với độ lợi dự đoán được tính toán tại 2
=
M
và đạt giá trị cao nhất tại 10=
M
. Các bậc lớn hơn 10 không cho được độ lợi cao hơn nữa, cho
nên ta có thể chỉ cần xét đến 10=
M
.
Hình 1.34 Độ lợi dự đoán (PG) là một hàm theo biến bậc dự đoán M