Tư duy mở trắc nghiệm toán lý
Sưu tầm và tổng hợp
(Đề thi có 12 trang)
135 CÂU VD TỔNG ÔN LƯỢNG GIÁC
Môn: Toán
Thời gian làm bài phút (135 câu trắc nghiệm)
Họ và tên thí sinh: .................................................... Mã đề thi 165
Câu 1. Số nghiệm của phương trình 2 sin x=√3trên đoạn 0; 5π
2là
A1.B3.C2.D4.
Câu 2. Tìm số nghiệm thuộc đoạn [2π; 4π]của phương trình sin 2x
cos x+ 1 = 0.
A5.B3.C6.D4.
Câu 3. Số nghiệm của phương trình 2 sin22x+ cos 2x+ 1 = 0 trong [0; 2018π]là
A2017.B2018.C1009.D1008.
Câu 4. Tìm số nghiệm của phương trình cos 2x−cos x−2 = 0 trong [0; 2π].
A1.B3.C2.D0.
Câu 5. Cho phương trình cos x+ sin 2x
cos 3x+ 1 = 0. Khẳng định nào dưới đây là đúng?
AĐiều kiện xác định của phương trình là cos x(3 + 4 cos2x)6= 0. .
BPhương trình đã cho vô nghiệm.
CNghiệm âm lớn nhất của phương trình là x=−π
2.
DPhương trình tương đương với phương trình (sin x−1) (2 sin x−1) = 0..
Câu 6. Số nghiệm thuộc đoạn h−π
2;π
2icủa phương trình cos x+ sin x=cos 2x
1−sin 2xlà
A4.B3.C2.D1.
Câu 7. Trong khoảng 0; π
2phương trình sin24x+ 3 sin 4x·cos 4x−4cos24x= 0 có bao nhiêu
nghiệm?
A4.B3.C1.D2.
Câu 8. Số điểm biểu diễn nghiệm của phương trình 8 cot 2xsin6x+ cos6x=1
2sin 4xtrên
đường tròn lượng giác là
A0.B4.C6.D2.
Câu 9. Gọi Tlà tập giá trị của hàm số y=1
2sin2x−3
4cos 2x+ 3. Tìm tổng các giá trị nguyên
của T.
A6.B4.C7.D3.
Câu 10. Số nghiệm của phương trình tan x+π
6=√3thuộc đoạn hπ
2; 2πilà
A2.B1.C4.D3.
Câu 11. Số nghiệm chung của hai phương trình 4 cos2x−3 = 0 và 2 sin x+ 1 = 0 trên khoảng
−π
2;3π
2bằng
A4.B3.C1.D2.
Câu 12. Cho phương trình 3√tan x+ 1(sin x+ 2 cos x) = m(sin x+ 3 cos x). Có tất cả bao nhiêu
giá trị nguyên của mthuộc đoạn [−2018; 2018] để phương trình trên có nghiệm duy nhất x∈
0; π
2?
Trang 1/12 −Mã đề 165
A2016.B4036.C2015.D2018.
Câu 13. Tìm nghiệm của phương trình cos2x−cos x= 0 thỏa mãn điều kiện 0< x < π.
Ax=π
2.Bx= 0.Cx= 2.Dx=π.
Câu 14. Cho phương trình sin2018 x+ cos2018 x= 2 sin2020 x+ cos2020 x. Tính tổng các nghiệm
của phương trình trong khoảng (0; 2018).
A(643)2π.B1285
42
π.C(642)2π.D1285
22
π.
Câu 15. Giá trị lớn nhất của hàm số y= 4 sin x+√2 cos 2xtrên đoạn 0; 3π
4.
A4−√2.B2√2.C√2.D4√2.
Câu 16. Tìm tất cả các giá trị thực của tham số mđể phương trình (cos x+1)(cos 2x−mcos x) =
msin2xcó đúng hai nghiệm x∈0; 2π
3.
A−1< m ≤ −1
2.B−√3
2≤m < 1.C−1< m ≤ −√3
2.D0≤m < 1.
Câu 17. Tìm số nghiệm thuộc −3π
2;πcủa phương trình √3 sin x= cos 3π
2−2x.
A2.B1.C0.D3.
Câu 18. Số nghiệm thuộc đoạn 0; 5π
2của phương trình 2 sin x−1 = 0.
A(−2; −1).B(1; 2).C(0; 1).D(−1; 0).
Câu 19. Bạn Trang có 10 đôi tất khác nhau. Sáng nay, trong tâm trạng vội vã đi thi, Trang đã
lấy ngẫu nhiên 4chiếc tất. Tính xác suất để trong 4chiếc tất lấy ra có ít nhất một đôi tất.
A224
323.B11
969.C6
19.D99
323.
Câu 20. Giá trị lớn nhất của mđể phương trình cos x+ sin2018 5x+m= 0 có nghiệm là
A−1.B0.C1.D3
2.
Câu 21. Phương trình sin x= cos xcó bao nhiêu nghiệm thuộc đoạn [−π;π]?
A3.B0.C2.D1.
Câu 22. Tìm điều kiện của tham số mđể phương trình m·sin x−3 cos x= 5 có nghiệm.
Am≤ −4hoặc m≥4.Bm≥√34.
Cm≥4.D−4≤m≤4.
Câu 23. Tìm mđể phương trình sin x+ (m−1) cos x= 2m−1có nghiệm.
A−1
3≤m≤1.Bm≥1
2.C
m > 1
m < −1
3
.D−1
2≤m≤1
3.
Câu 24. Hàm số y= sin4x+ cos4xcó tập giá trị là T= [a;b]. Giá trị của b−alà
A1
2.B1
4.C4.D1.
Câu 25. Biểu diễn tập nghiệm của phương trình cos x+cos 2x+cos 3x= 0 trên đường tròn lượng
giác ta được số điểm là
A4.B2.C5.D6.
Trang 2/12 −Mã đề 165
Câu 26. Giải phương trình cos 3x·tan 4x= sin 5x.
Ax=k2π,x=π
16 +k3π
8.Bx=kπ
2,x=π
16 +k3π
8.
Cx=k2π
3,x=π
16 +kπ
8.Dx=kπ,x=π
16 +kπ
8.
Câu 27. Có tất cả bao nhiêu giá trị nguyên của tham số mđể phương trình cos32x−cos22x=
msin2xcó nghiệm thuộc khoảng 0; π
6?
A3.B1.C2.D0.
Câu 28. Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h(m) của con
kênh tính theo thời gian t(giờ) trong một ngày được cho bởi công thức: h=1
2cos πt
8+π
4+ 3.
Thời điểm mực nước của kênh cao nhất là
At= 16.Bt= 15.Ct= 14.Dt= 13.
Câu 29. Tìm mđể phương trình sin 4x=m·tan xcó nghiệm x6=kπ
A−1
2≤m < 4.B−1
2< m < 4.C−1< m < 4.D−1
2≤m≤4.
Câu 30. Phương trình 2 sin2x+ 3 sin x+m= 0 có nghiệm khi
Am≥9
8.Bm≤ −5.Cm≤1.D−5≤m≤9
8.
Câu 31. Cho phương trình 21−3 sin2xcos2x−sin xcos x
√2−2 sin x= 0 có x0là nghiệm dương lớn
nhất trên khoảng (0; 100π)và có dạng x0=aπ +π
b(a, b ∈Z). Tính tổng T=a+b.
AT= 102.BT= 100.CT= 103.DT= 101.
Câu 32. Tổng các nghiệm của phương trình 2 cos2x+√3 sin 2x= 3 trên 0; 5π
2là
A2π.B7π
2.C7π
6.D7π
3.
Câu 33. Tìm tập hợp tất cả giá trị của tham số thực mđể phương trình sin2x+ sin xcos x=m
có nghiệm.
A"1−√2
2;1 + √2
2#.B−1
4;1
4.
C[−√2; √2].D"2−√2
2;2 + √2
2#.
Câu 34. Giá nhị nhỏ nhất của hàm số y= cos 2x−4 cos x+ 6 là
A3.B6.C11.D5.
Câu 35. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y=sin x+ cos x
2 sin x−cos x+ 3 lần lượt là
A1và 2.B−1và 2.C−1và 1
2.D−1
2và 1.
Câu 36. Phương trình 4 sin22x−3 sin 2xcos 2x−cos22x= 0 có bao nhiêu nghiệm trong khoảng
(0; π)?
A2.B3.C1.D4.
Câu 37. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=2 + cos x
sin x+ cos x+ 2 là
A2
3.B5.C3.D3
2.
Trang 3/12 −Mã đề 165
Câu 38. Từ các số 1; 2; 3; 4 ta lập số gồm 4chữ số khác nhau từng đôi. Tổng của tất cả các số
lập được là
A66660.B5660.C3660.D6660.
Câu 39. Tìm mđể phương trình (cos x+ 1) (2 cos2x−1−mcos x)−msin2x= 0 có đúng hai
nghiệm thuộc 0; 2π
3.
A0< m ≤1
2.B−1
2< m ≤1.C−1< m ≤ −1
2.D−1< m ≤1.
Câu 40. Phương trình sin 5x+ sin 9x+ 2 sin2x−1 = 0 có một họ nghiệm là
Ax=π
42 +k2π
3.Bx=π
42 +k2π
7.Cx=π
5+k2π.Dx=3π
7+kπ.
Câu 41. Cho phương trình (cos x+ 1)(cos 2x−mcos x) = msin2x. Phương trình có đúng hai
nghiệm thuộc đoạn 0; 2π
3khi
A−1< m ≤ −1
2.Bm≥ −1.C−1≤m≤1.Dm > −1.
Câu 42. Xét phương trình sin 3x−3 sin 2x−cos 2x+ 3 sin x+ 3 cos x= 2. Phương trình nào dưới
đây tương đương với phương trình đã cho?
A(2 sin x−1)(2 cos2x+ 3 cos x+ 1) = 0.B(2 sin x−cos x+ 1)(2 cos x−1) = 0.
C(2 sin x−1)(2 cos x−1)(cos x−1) = 0.D(2 sin x−1)(2 cos x+ 1)(cos x−1) = 0.
Câu 43. Phương trình cos 4x
cos 2x= tan 2xcó số nghiệm thuộc khoảng 0; π
2là bao nhiêu?
A2.B4.C1.D3.
Câu 44. Số nghiệm của phương trình cos2x−sin 2x=√2 + cos2π
2+xtrên khoảng (0; 3π)
bằng
A1.B4.C2.D3.
Câu 45. Tính tổng Scác nghiệm của phương trình (2 cos 2x+ 5)(sin4x−cos4x) + 3 = 0 trong
khoảng (0; 2π).
AS=11π
6.BS=7π
6.CS= 5π.DS= 4π.
Câu 46. Phương trình cos2x+ cos x−2 = 0 có bao nhiêu nghiệm trong đoạn [0; 2π].
A4.B1.C2.D3.
Câu 47. Cho phương trình (1 + sin 2x) cos x−(1 + cos 2x) sin x= sin 2x. Tính tổng các nghiệm
của phương trình trên khoảng (0; π).
A0.B2π
3.Cπ.D3π
2.
Câu 48. Với giá trị lớn nhất của abằng bao nhiêu để phương trình asin2x+2 sin 2x+3acos2x= 2
có nghiệm?
A4.B2.C8
3.D11
3.
Câu 49. Phương trình (1 + cos 4x) sin 2x= 3 cos22xcó tổng các nghiệm trong đoạn [0; π]là.
A3π
2.B2π
3.Cπ
3.Dπ.
Câu 50. Có bao nhiêu giá trị thực của mđể phương trình (sin x−1)(2 cos2x−(2m+1) cos x+m) =
0có đúng bốn nghiệm thực phân biệt thuộc đoạn [0; 2π].
A1.B3.C4.D2.
Trang 4/12 −Mã đề 165
Câu 51. Cho phương trình sin x−√3 cos x= 2 sin 3x. Gọi x1và x2lần lượt là nghiệm lớn nhất
và nhỏ nhất của phương trình đã cho trong đoạn [0; 2018π]. Tính tổng x1+x2.
Ax1+x2=12107π
6.Bx1+x2=12103π
6.
Cx1+x2=12109π
6.Dx1+x2=12111π
6.
Câu 52. Tìm mđể phương trình √1−sin x+rsin x+1
2=mcó nhiệm.
A1
2≤m≤√6
2.B0≤m≤1.C0≤m≤√3.D√6
2≤m≤√3.
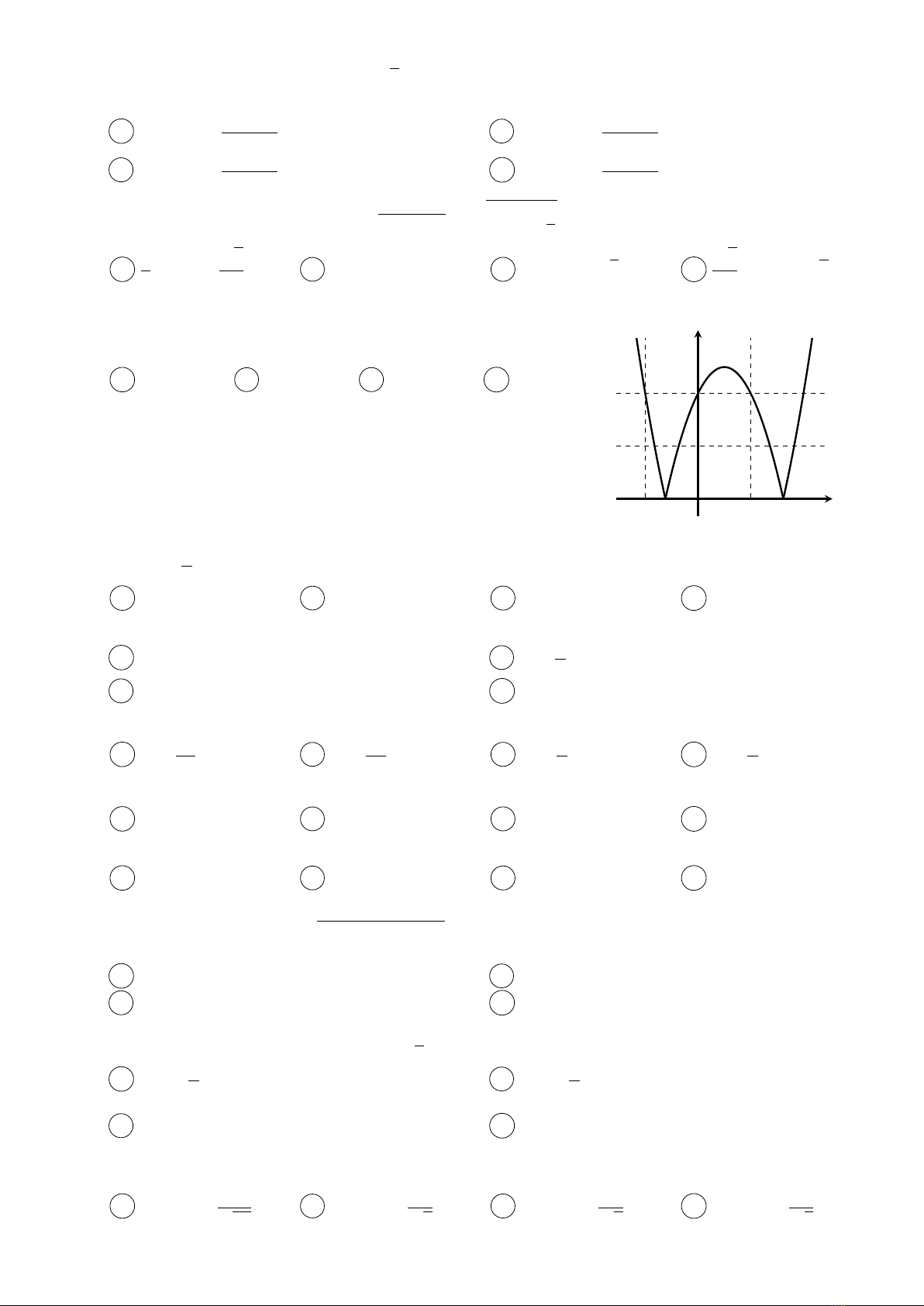
Câu 53.
Cho hàm số y=f(x) = |x2−2x−4|có đồ thị như hình vẽ.
Hàm số y=f(x)có bao nhiêu cực trị?
A2.B1.C4.D3.
x
y
O
2
4
-2 2 4
Câu 54. Có bao nhiêu số nguyên msao cho phương trình msin x+ 4 cos x= 4 có nghiệm trong
khoảng 0; π
3?
A3.B5.C2.D4.
Câu 55. Nghiệm của phương trình cos 2x−5 cos x+ 4 = 0 là
Ax=k2π, k ∈Z.Bx=π
2+k2π, k ∈Z.
Cx=kπ, k ∈Z.Dx=π+k2π, k ∈Z.
Câu 56. Nghiệm dương bé nhất của phương trình: 2 sin2x+ 5 sin x−3 = 0 là:
Ax=3π
2.Bx=5π
6.Cx=π
2.Dx=π
6.
Câu 57. Có bao nhiêu giá trị nguyên của mđể phương trình cos 2x−4 cos x−m= 0 có nghiệm?
A6.B8.C9.D7.
Câu 58. Tìm tổng tất cả các nghiệm của phương trình cos(sin x) = 1 thuộc đoạn [0; 2π].
A2π.B3π.Cπ.D0.
Câu 59. Cho phương trình msin x+ cos x
2 + sin x+ cos x= 1.Tìm tất cả giá trị tham số mđể phương trình
có nghiệm.
A−1≤m∨m > 1.Bm < −1∨m > 3.
Cm≤ −1∨m≥3.D−1≤m≤3.
Câu 60. Phương trình cos (2x−30◦) = 1
2có các họ nghiệm là
Ax=±π
6+ 15◦+k180◦,(k∈Z).Bx=±π
3+ 30◦+k180◦,(k∈Z).
C"x= 45◦+k360◦
x=−15◦+k360◦(k∈Z).D"x= 45◦+k180◦
x=−15◦+k180◦(k∈Z).
Câu 61. Cho góc tù xthỏa mãn 14 cos2x+ sin 2x= 2. Khi đó cos xbằng
Acos x=−1
√10.Bcos x=±1
√5.Ccos x=−1
√5.Dcos x=−1
√3.
Trang 5/12 −Mã đề 165