Lưu Văn Biền - GV Trường THPT Hiệp Hòa 1 - Bắc Giang
20 BÀI TÍCH PHÂN
I. LÍ THUYẾT
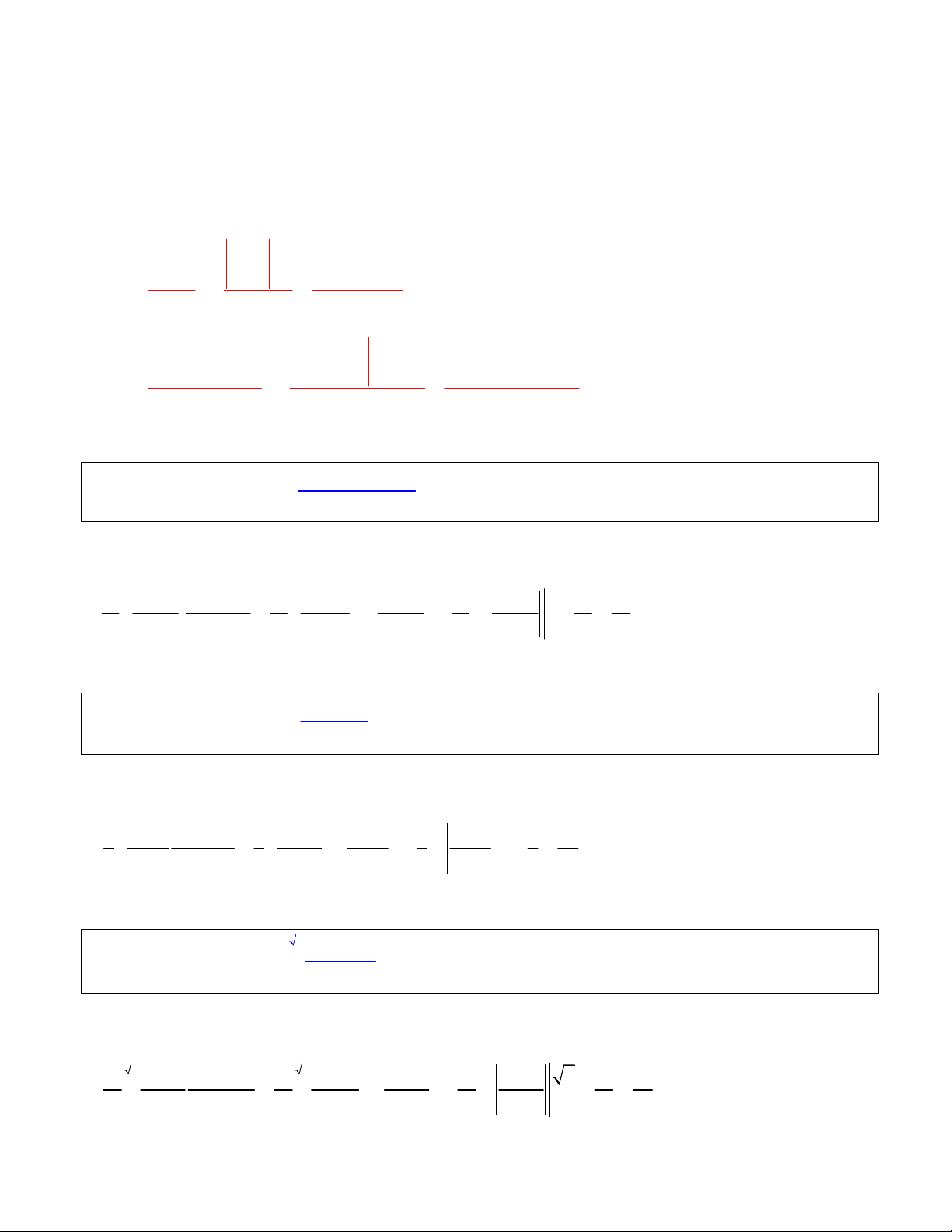
Trong bài viết có sử dụng hai công thức sau:
1.
2 2
a b dx
ad bc dx
c d
ax b
dcx d cx d cx d
2.
2 2
sin cos
sin cos sin cos sin cos
a b dx
ad bc dx
c d
a x b x
dc x d x
c x d x c x d x
II. BÀI TẬP
Bài 1. Tính tích phân
1
1
0
2 3 3 1
dx
Ix x
Lời giải
1 1
12
0 0
1
1 3 1 11. 1 1 2 3 1 2 3 1 1
. . ln ln
2 3 0
11 2 3 11 3 1 11 3 1 11 12
3 1
3 1
x dx x x
I d
x
x x x
x
x
Bài 2. Tính tích phân
4
23
2
1
dx
Ix x
Lời giải
4 4
3 2 3 3
22 3
3 3 3
3
2 2 3
4
1 1 3 1 1 1 1 72
ln ln
2
3 3 1 3 1 3 65
1
1
x x dx x x
I d
x
x x x
x
x
Bài 3. Tính tích phân
7
32
1
9
dx
Ix x
Lời giải
7 7
2 2 2
32 2
2 2 2
2
1 1 2
1 9 18 1 1 1 1 35
7
ln ln
18 18 9 18 9 18 8
1
9
9
x xdx x x
I d
x
x x x
x
x
Lưu Văn Biền - GV Trường THPT Hiệp Hòa 1 - Bắc Giang
Bài 4. Tính tích phân
43
44
1
Ix x
Lời giải
4 4 4
3 3 3
4 3 4 4 4
42 4
4 4 4
44
1 1 1 4
1 1 4 1 1 1 1 3
3
ln ln
4 4 1 4 1 4 2
11
1
1
dx x x dx x x
I d
x
x x x
x x x
x
Bài 5. Tính tích phân
22
52 2
1
1
1 3 1
x
I dx
x x x x
Lời giải
2
2 2
2 2 2
52 2
2 2 2
2
1 1 2
4 1 2
1 3 1 1 1 1 1 1 1 15
. . ln ln
11
4 1 4 3 1 4 3 1 4 11
3 1
3 1
x dx
x x x x x x
I d
x x
x x x x x x
x x
x x
Bài 6. Tính tích phân
1
63
0
1
1
x
x
Lời giải
2
1 1
62
0 0
1
1 1 2. 1 1 1 1 1 1
. . 0
2 1 2 1 1 4 1 4
1
x dx x x x
I d
x x x x
x
Bài 7. Tính tích phân
1
73
02 1
x
I dx
x
Lời giải
2
1 1
72
0 0
1
1 1
. . 0
2 1 2 1 2 1 2 2 1 18
2 1
x dx x x x
I d
x x x x
x
Bài 8. Tính tích phân
4
8
11
dx
I
x x
Lời giải
Lưu Văn Biền - GV Trường THPT Hiệp Hòa 1 - Bắc Giang
4 4
82
1 1
4
1 1 4
2 . 2 . 2ln 2ln
1
3
1 1
2 1
1
x dx x x
I d
x x x x
x x
x
Bài 9. Tính tích phân
9
1
1x
x
I dx
x xe
Lời giải
92
1
1 1
. ln
1 1
1
1
x
x x x
x
x x x
x
x
x e dx
xe xe xe
I d C
xe
xe xe xe
xe
xe
Bài 10. Tính tích phân
10 3
1
1 ln ln
1 ln
e
x x
I dx
x x
Lời giải
22
10
2 2
1 1
1 ln ln . 1 ln 1 ln 1 1 ln 4 12
. . 1
1 ln 1 ln 1 ln 2 1 ln
1 ln 8 2
e e e
x x dx x x x e e
I d
x x x x x x x x
x x e
Bài 11. Tính tích phân
11
2
2sin 3cos
dx
I
x x
Lời giải
Ta có
2
3 2
sin cos
2sin 3cos 2sin 3cos
a b dx
a x b x
dx x
x x
. Do đó, nếu chọn
1
a b
thì ta được:
11
sin cos sin cos
2sin 3cos 2sin 3cos
x x x x
I d C
x x x x
Nhận xét. Nếu chọn
1, 0
a b
thì ta được 11
1 sin 1 sin
.
3 2sin 3cos 3 2sin 3cos
x x
I d C
x x x x
Bài 12. Tính tích phân
2
12 3
0
sin
sin 3 cos
x
I dx
x x
Lời giải
Lưu Văn Biền - GV Trường THPT Hiệp Hòa 1 - Bắc Giang
2 2
12 2
0 0
1 sin 3. 1 sin sin
. .
3 sin 3 cos 3 sin 3 cos sin 3 cos
sin 3 cos
x dx x x
I d
x x x x x x
x x
2
1 sin 3
2
6
2 3 sin 3 cos 0
x
x x
Bài 13. Tính tích phân
2
13 3
0
3sin 2cos
sin cos
x x
I dx
x x
Lời giải
2 2
13 2
0 0
1 3sin 2cos 5. 1 3sin 2cos 3sin 2cos
. .
5 sin cos 5 sin cos sin cos
sin cos
x x dx x x x x
I d
x x x x x x
x x
2
1 3sin 2cos 1
2
10 sin cos 2
0
x x
x x
Bài 14. Tính tích phân
14
1
1
ln
ex
x
xe
I dx
x e x
Lời giải
14
1
ln
ln ln ln 1 1
1
ln
x
e
x e
x
d e x e
I e x e
e x
Bài 15. Tính tích phân
2
15 2 2
0
sin 2
2006 cos 4sin
x
A I dx
x x
Lời giải
22 2 2 2
15
0
2 2 2
cos 4sin cos 4sin 2
3 3 3
0
I d x x x x
Bài 16. Tính tích phân
3
16 2
4
tan
cos 1 cos
x
I dx
x x
Lưu Văn Biền - GV Trường THPT Hiệp Hòa 1 - Bắc Giang
Lời giải
3 3 3 2 2
16 2 2
2
4 4 4
2
tan tan 3
2 tan 2 tan 5 3
1cos 2 tan
cos cos 1 4
cos
x x
I dx dx d x x
x x
x x x
Bài 17. Tính tích phân
1
2
17
0
ln 1
I x x dx
Lời giải
1 1 1
2 2 2
2 2 2
17
0 0 0
1
1 1 1 1
ln 1 ln 1 ln 1 ln 2 ln 2
0
2 2 2 2
x x x
I x d x d x xdx
Bài 18. Tính tích phân
3
18 2
1
3 ln
2009 1
x
B I dx
x
Lời giải
3 3 3 3
18 2
1 1 1 1
3
3 ln 3 3
3 ln 3 ln 3 ln ln3
1
1 1 1 4 4 1
1
x x x x dx
I dx x d x d x
x x x x
x
3
3 3 3 3
ln3 ln 1 ln3 ln 2
1
4 4 4 4
x
Bài 19. Tính tích phân
13
19 4 2
0
2012
3 2
x
B I dx
x x
Lời giải
2
2 2 2 2 2
1 1 1 1 1
19 2 2 2 2 2
2 2
0 0 0 0 0
2 1 2 2 1 2 1
2 1 1 1 9
. ln ln
0
2 1 2 2 1 2 1 2 8
1 2
x x d x d x x
xdx xdx
I xdx x x x x x
x x
Bài 20. Tính tích phân
ln5
20
ln3
2006
2 3
x x
dx
B I e e
Lời giải