Đề số 1
ĐỀ ÔN TẬP HỌC KÌ 2 – Năm học
Môn TOÁN Lớp 10
Thời gian làm bài 90 phút
Câu 1:
1) Cho ba số dương a, b, c. Chứng minh:
2) Giải các bất phương trình sau:
a) b)
Câu 2:
a) Tính các giá trị lượng giác sin2, cos2 biết cot = 3 và .
b) Cho biết . Tính giá trị của biểu thức :
Câu 3: Trong mặt phẳng toạ độ Oxy, cho A(–1; 2), B(3; –5), C(–4; –9).
a) Tính độ dài các cạnh của tam giác ABC.
b) Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác.
c) Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Câu 4: Cho ABC có , AC = 8 cm, AB = 5 cm.
a) Tính cạnh BC.
b) Tính diện tích ABC.
c) Chứng minh góc nhọn.
d) Tính bán kính đường tròn nội tiếp và ngoại tiếp tam giác ABC.
e) Tính đường cao AH.
--------------------Hết-------------------
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
a b c ab bc ca
x x
2 5 1
x
x x
2
3 14
1
3 10
7
4
2
tan 3
2sin cos
sin 2cos
µ
A
0
60
B
$
Đề số 1
ĐÁP ÁN ĐỀ ÔN TẬP HỌC KÌ 2 – Năm học
Môn TOÁN Lớp 10
Thời gian làm bài 90 phút
Câu 1:
1) Cho ba số dương a, b, c. Chứng minh:
Áp dụng bất đẳng thức Cô-si, ta có:
Cộng các bất đẳng thức trên, vế theo vế, rồi chia cho 2 ta được:
Dấu bằng xảy ra khi và chỉ khi a = b = c
2) Giải các bất phương trình sau:
a)
b)
Câu 2:
a) Tính các giá trị lượng giác sin2, cos2 biết cot = 3 và .
b) Cho biết . Tính giá trị của biểu thức:
Vì
Câu 3: Trong mặt phẳng toạ độ Oxy, cho A(–1; 2), B(3; –5), C(–4; –9).
a) Tính độ dài các cạnh của tam giác ABC.
ABC vuông cân tại B.
b) Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác.
Diện tích tam giác ABC là (đvdt)
a b c ab bc ca
a b ab b c bc c a ac
2 , 2 , 2
a b c ab bc ca
x
x
x x x
x x x x
14
1
2 5 1 ;6
4
1 2 5 1 63
3
x x x x
x x x x
22
2 2
3 14 4
1 0 3 10 0
3 10 3 10
x
5 2
7
4
2
2 2
2
1 1 9
sin cos
10 10
1 cot
2
9 4
cos2 2cos 1 2. 1
10 5
2
2
7 4 3
4 7 2 8 sin2 0 sin2 1 cos 2 1
2 5 5
tan 3
2sin cos
sin 2cos
2sin cos 2tan 1
tan 3 cos 0 7
sin 2cos tan 2
AB AC BC AB AC BC
2 2 2
(4; 7), ( 3; 11), ( 7; 4) 65, 130, 65
uur uuur uuur
AB AC BC
65, 130; 65
S AB BC
1 65.65 65
.
2 2 2
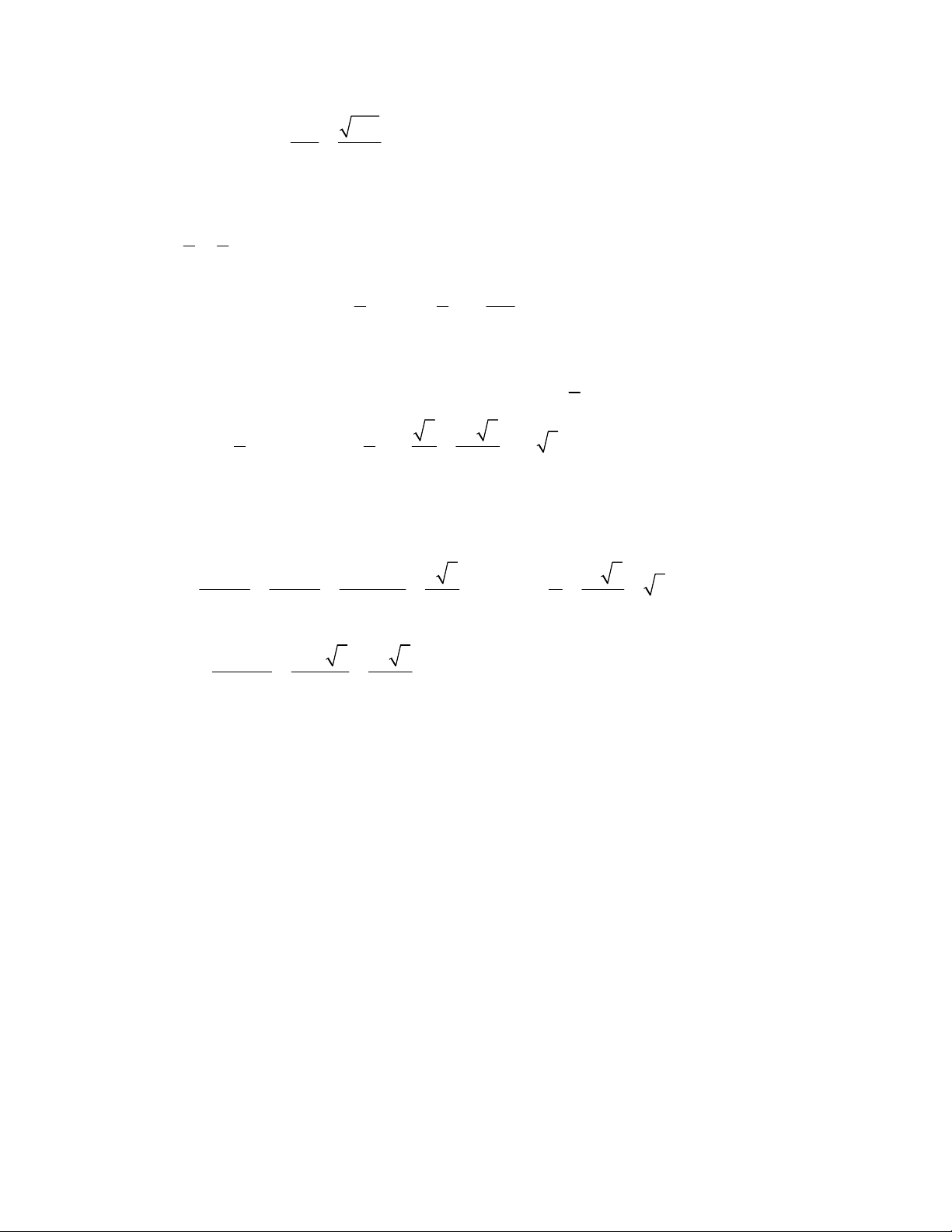
Bán kính R =
c) Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm I của AC
PT đường tròn:
Câu 4: Cho ABC có , AC = 8 cm, AB = 5 cm.
a)
b) (đvdt)
c) Chứng minh góc nhọn.
Ta có: nhọn
d) Tính bán kính đường tròn nội tiếp và ngoại tiếp tam giác ABC.
e) Tính đường cao AH.
====================
AC
130
2 2
I
5 7
;
2 2
x y
2 2
5 7 130
2 2 4
µ
A
0
60
BC AB AC AB AC A BC
2 2 2 1
2 . .cos 64 25 2.8.5. 49 7
2
ABC
S AB AC A
1 1 3 20 3
. .sin .8.5. 10 3
2 2 2 2
B
$
AB BC AC
2 2 2
74 64
B
$
a BC
RA A 0
7 7 3
2sin 2sin 3
2sin60
S
rp
10 3
3
10
ABC
S
AH
BC
2
2.10 3 20 3
7 7
Đề số 2
ĐỀ ÔN TẬP HỌC KÌ 2 – Năm học
Môn TOÁN Lớp 10
Thời gian làm bài 90 phút
Câu 1: Cho . Tìm m để:
a) Phương trình f(x) = 0 có 2 nghiệm trái dấu
b) Bất phương trình f(x) 0 có tập nghiệm R
Câu 2: Giải hệ bất phương trình
Câu 3:
a) Chứng minh biểu thức sau đây không phụ thuộc vào .
b) Cho P = và
Tính P + Q = ?
Câu 4: Trong mặt phẳng toạ độ Oxy, cho đường tròn có phương trình:
a) Xác định toạ độ tâm và tính bán kính của đường tròn.
b) Lập phương trình tiếp tuyến của đường tròn, biết tiếp tuyến song song với
đường thẳng d có phương trình: .
--------------------Hết-------------------
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
f x x m x m m
2 2
( ) 2( 2) 2 10 12
x x
x x
x
2
2
8 15 0
12 64 0
10 2 0
A
2 2
2
cot 2 cos 2 sin2 .cos2
cot 2
cot 2
sin( ) cos( )
Qsin sin
2
x y x y
2 2
2 4 4 0
x y
3 4 1 0
Đề số 2
ĐÁP ÁN ĐỀ ÔN TẬP HỌC KÌ 2 – Năm học
Môn TOÁN Lớp 10
Thời gian làm bài 90 phút
Câu 1: Cho . Tìm m để:
a) PT f(x) = 0 có 2 nghiệm trái dấu
b) f(x) 0 có tập nghiệm R
Câu 2:
Câu 3:
a)
b) Ta có P = = ,
Vậy P + Q =
Câu 4: (C):
a) nên tâm , bán kính R = 3.
b) Vì tiếp tuyến // d: nên PTTT có dạng:
và
Vậy có hai tiếp tuyến thỏa mãn đề bài là
f x x m x m m
2 2
( ) 2( 2) 2 10 12
ac m m m
2
0 2 10 12 0 ( 3; 2)
am m m
2 2
0
' ( 2) (2 10 12) 0
' 0
m m m
2
6 8 0 ( ; 4] [ 2; )
 
x x x
x x x x
x x
2
2
8 15 0 ( ;3] [5; )
12 64 0 [ 4;16] [ 4;3]
10 2 0 ( ;5]
 

A
2 2 2 2
2
cot 2 cos 2 sin2 .cos2
1 sin 2 sin 2 1
cot 2
cot 2
sin( ) cos( )
sin cos
Q
sin sin cos .sin
2
sin2
x y x y
2 2
2 4 4 0
x y x y x y
2 2 2 2
2 4 4 0 ( 1) ( 2) 9
I
(1; 2)
x y
3 4 1 0
x y C C
3 4 0, 1
CC
d I R C C
2 2
3.1 4.( 2)
4
( , ) 3 11 15
26
3 4
x y x y
1 2
: 3 4 4 0, : 3 4 26 0